Однофакторный дисперсионный анализ используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп.
В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ на калькуляторе TI-84.
Пример. Однофакторный дисперсионный анализ на калькуляторе TI-84.
Предположим, мы набираем 30 студентов для участия в исследовании. Студентам случайным образом назначают использовать один из трех методов обучения в течение одного месяца для подготовки к экзамену. В конце месяца все студенты сдают одинаковый тест.
Используйте следующие шаги, чтобы выполнить однофакторный дисперсионный анализ, чтобы определить, одинаковы ли средние баллы для всех трех групп.
Шаг 1: Введите данные.
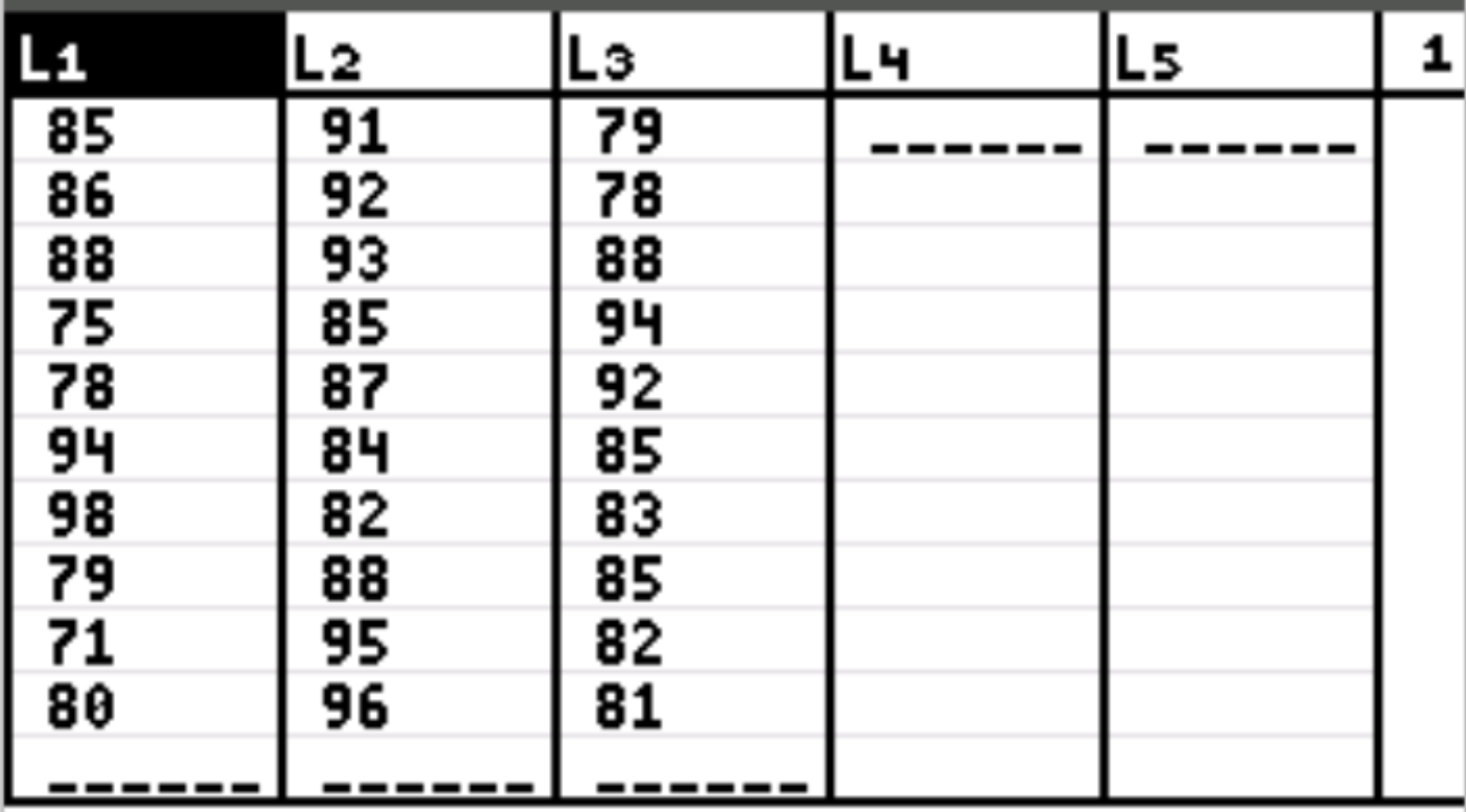
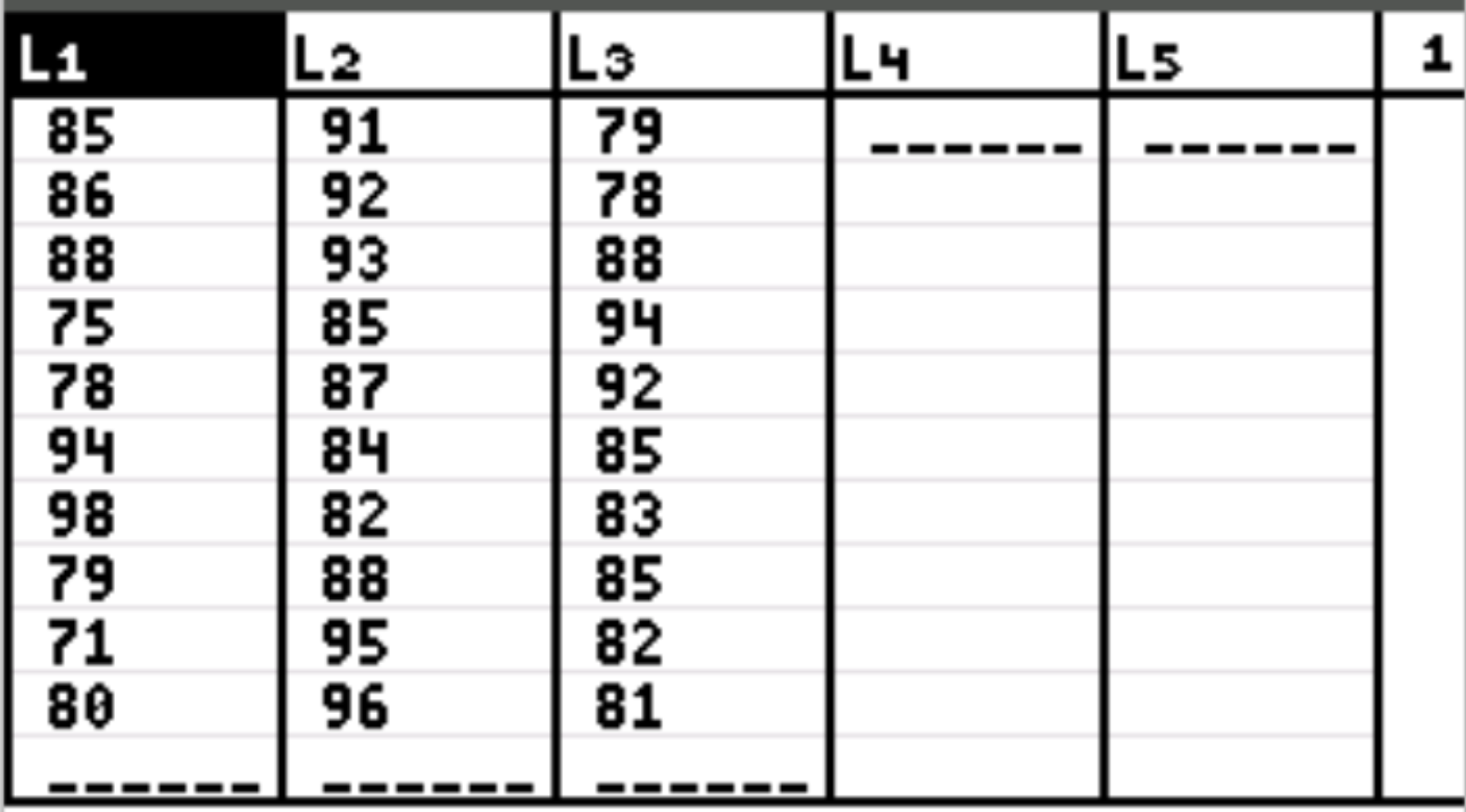
Сначала мы введем значения данных как для объясняющей, так и для ответной переменной. Нажмите Stat, а затем нажмите EDIT.Введите следующие экзаменационные баллы для студентов, которые использовали первый метод обучения в столбце L1, второй метод обучения в столбце L2 и третий метод обучения в столбце L3:
Шаг 2: Выполните односторонний ANOVA.
Далее мы выполним односторонний ANOVA. Нажмите Stat, а затем прокрутите до TESTS.Затем прокрутите вниз до ANOVA и нажмите Enter .
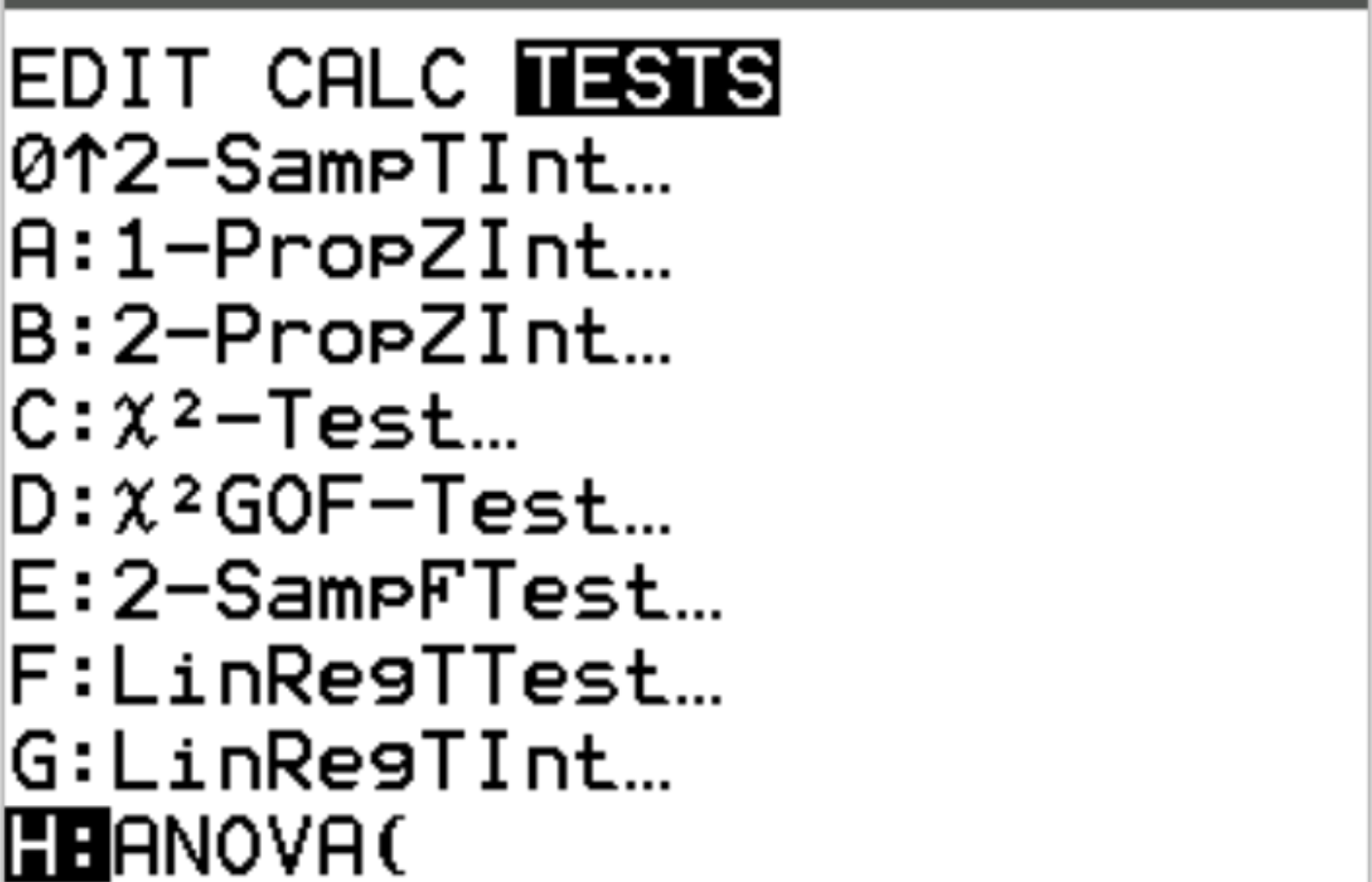
Введите списки, в которых хранятся данные, через запятую, затем добавьте закрывающую скобку ) и нажмите Enter .
Примечание. Чтобы отобразить L1, нажмите 2nd , а затем 1.Чтобы появился L2, нажмите 2nd , а затем 2.Чтобы появился L3, нажмите 2 , а затем нажмите 3 .

После нажатия Enter появятся следующие результаты:
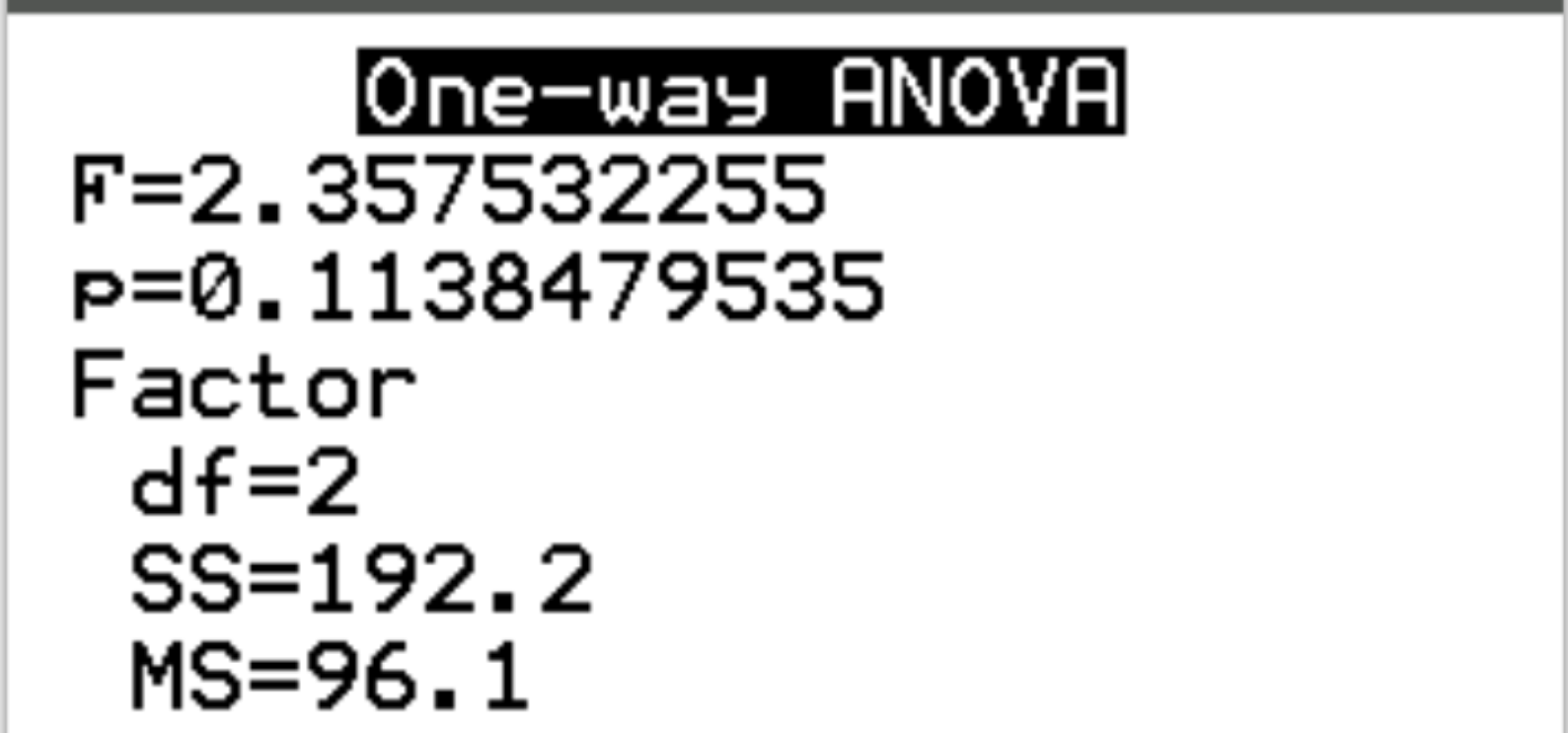
Шаг 3: Интерпретируйте результаты.
F-статистика для теста равна 2,3575 , а соответствующее p-значение равно 0,1138.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Таким образом, у нас нет достаточных доказательств, чтобы сказать, что средний балл экзамена различается между тремя группами. То есть у нас нет достаточных оснований утверждать, что методика обучения приводит к разным экзаменационным баллам.