В статистике две переменные подчиняются двумерному нормальному распределению , если они имеют нормальное распределение при сложении.
В этом руководстве объясняется, как выполнять следующие задачи в R:
- Симулируйте двумерное нормальное распределение
- Постройте двумерное нормальное распределение, используя контурный график (двухмерный график)
- Постройте двумерное нормальное распределение, используя поверхностный график (трехмерный график)
Давайте прыгать!
Пример 1. Моделирование двумерного нормального распределения в R
Самый простой способ смоделировать двумерное нормальное распределение в R — использовать функцию mvrnorm() из пакета MASS .
Следующий код показывает, как использовать эту функцию для имитации двумерного нормального распределения на практике:
library (MASS)
#make this example reproducible
set. seed ( 0 )
#simulate bivariate normal distribution
bivariate_data <- as. data.frame (mvrnorm(n= 100 ,
mu=c(0, 0),
Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))
#view first six rows of bivariate dataset
head(bivariate_data)
V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238
Вот что делает каждый аргумент в функции mvrnorm() :
- n : определяет размер выборки
- mu : определяет среднее значение каждой переменной
- Сигма : определяет ковариационную матрицу двух переменных.
Конечным результатом является фрейм данных с двумя переменными, которые после сложения подчиняются нормальному распределению.
Пример 2. Постройте двумерное нормальное распределение
Самый простой способ построить двумерное нормальное распределение в R — использовать функции из пакета mnormt() .
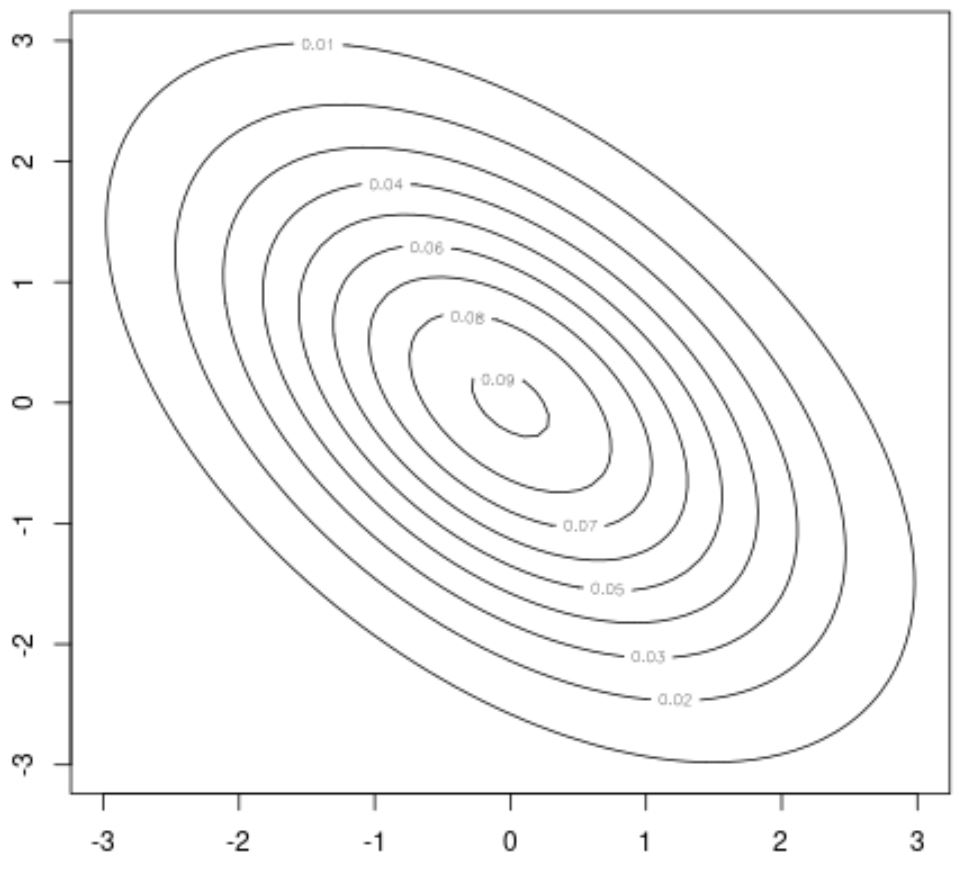
Например, мы можем использовать функцию контура () из этого пакета для создания контурного графика, который предлагает двухмерную визуализацию двумерного нормального распределения:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create contour plot
contour(x, y, z)

Мы также можем использовать функцию persp() для создания поверхностного графика, который предлагает трехмерную визуализацию двумерного нормального распределения:
library (mnormt)
#make this example reproducible
set. seed ( 0 )
#create bivariate normal distribution
x <- seq(-3, 3, 0.1)
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)
#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype='detailed')
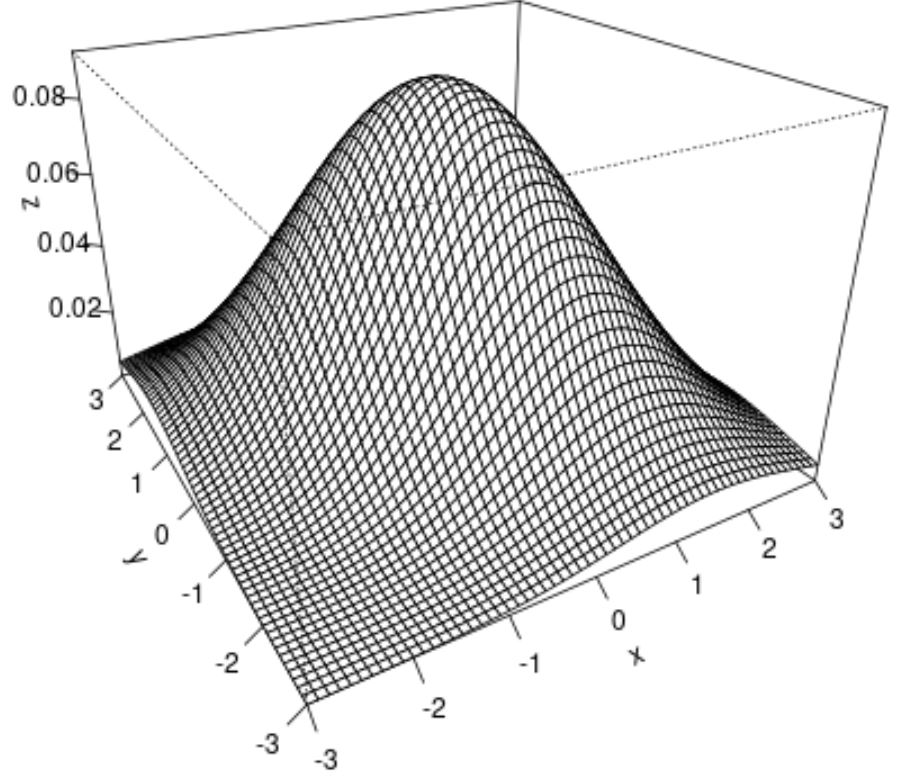
Вот что делает каждый аргумент в функции persp() :
- theta, phi : определяет углы направления обзора.
- expand : Управляет размером оси Z.
- ticktype : Управляет появлением делений на осях.
Конечным результатом является трехмерный график поверхности двумерного нормального распределения.
Дополнительные ресурсы
В следующих руководствах объясняется, как работать с другими распределениями вероятностей в R:
Как использовать нормальное распределение в R
Как использовать биномиальное распределение в R
Как использовать распределение Пуассона в R
Как использовать полиномиальное распределение в R