В статистике z-показатель говорит нам, на сколько стандартных отклонений значение отличается от среднего.Мы используем следующую формулу для расчета z-показателя:
z = (X - μ) / σ
где X — значение, которое мы анализируем, μ — среднее значение, а σ — стандартное отклонение.
Z-оценка может быть положительной, отрицательной или равной нулю.
Положительный z-показатель указывает, что конкретное значение больше среднего, отрицательный z-показатель указывает, что конкретное значение меньше среднего, а нулевой z-показатель указывает, что конкретное значение равно среднему.
Несколько примеров должны прояснить это.
Примеры: расчет Z-показателя
Предположим, у нас есть следующий набор данных, показывающий высоту (в дюймах) определенной группы растений:
5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20
Среднее значение выборки этого набора данных равно 13 , а стандартное отклонение выборки равно 5,51 .
1. Найдите z-оценку для значения «8» в этом наборе данных.
Вот как рассчитать z-оценку:
z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91
Это означает, что значение «8» на 0,91 стандартного отклонения ниже среднего.
2. Найдите z-показатель для значения «13» в этом наборе данных.
Вот как рассчитать z-оценку:
z = (X – μ) / σ = (13 – 13) / 5,46 = 0
Это означает, что значение «13» точно равно среднему значению.
3. Найдите z-показатель для значения «20» в этом наборе данных.
Вот как рассчитать z-оценку:
z = (X - μ) / σ = (20 - 13) / 5,46 = 1,28
Это означает, что значение «20» на 1,28 стандартного отклонения выше среднего.
Как интерпретировать Z-показатели
Z-таблица сообщает нам, какой процент значений находится ниже определенных Z-показателей. Несколько примеров должны прояснить это.
Пример 1: Отрицательные Z-показатели
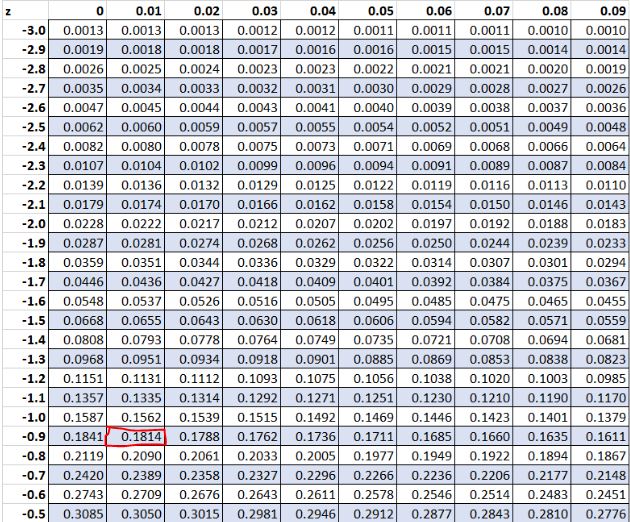
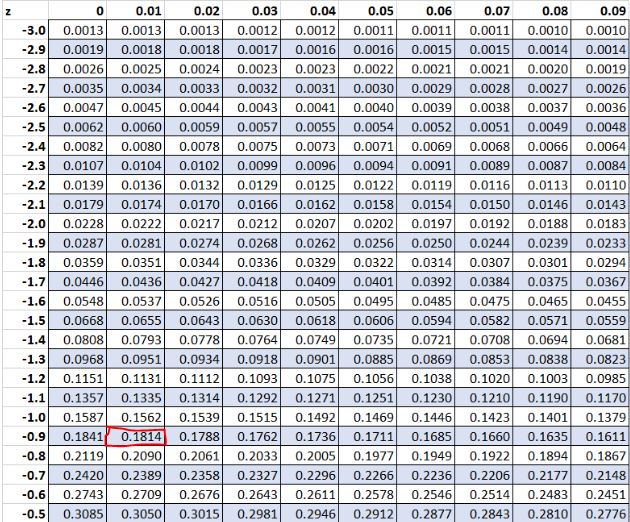
Ранее мы обнаружили, что необработанное значение «8» в нашем наборе данных имело z-показатель -0,91.Согласно таблице Z, 18,14% значений опускаются ниже этого значения.
Пример 2: Z-показатели равны нулю
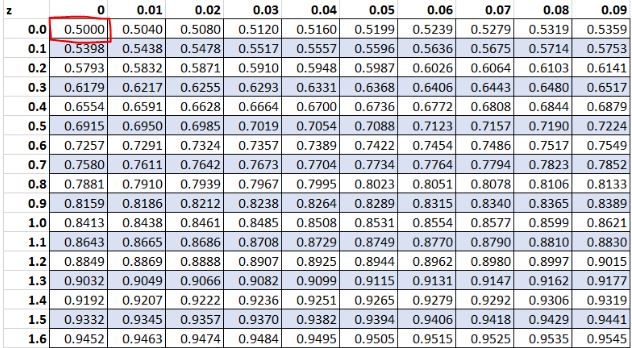
Ранее мы обнаружили, что необработанное значение «13» в нашем наборе данных имело z-оценку 0.Согласно таблице Z, 50,00% значений находятся ниже этого значения.
Пример 3: положительные Z-показатели
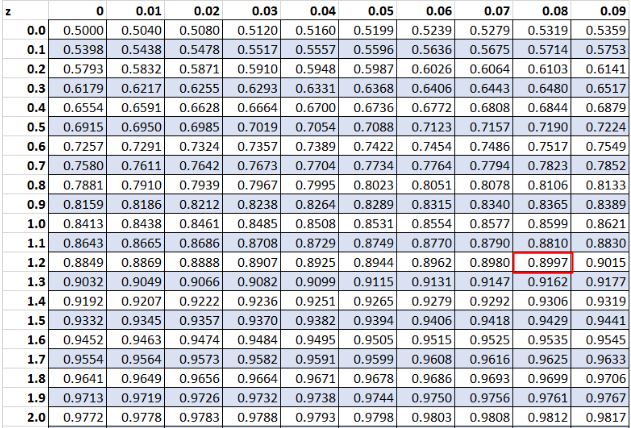
Ранее мы обнаружили, что необработанное значение «20» в нашем наборе данных имело z-показатель 1,28.Согласно таблице Z, 89,97% значений находятся ниже этого значения.
Вывод
Z-показатели могут принимать любое значение между отрицательной бесконечностью и положительной бесконечностью, но большинство z-показателей находятся в пределах 2 стандартных отклонений от среднего. На самом деле в статистике есть правило, известное как эмпирическое правило , которое гласит, что для данного набора данных с нормальным распределением:
- 68% значений данных находятся в пределах одного стандартного отклонения от среднего.
- 95% значений данных находятся в пределах двух стандартных отклонений от среднего значения.
- 99,7% значений данных находятся в пределах трех стандартных отклонений от среднего значения.
Чем выше абсолютное значение z-показателя, тем дальше исходное значение от среднего значения набора данных. Чем ниже абсолютное значение z-показателя, тем ближе исходное значение к среднему значению набора данных.
Похожие темы:
Калькулятор эмпирических правил
Как применить эмпирическое правило в Excel