Точечный график — это тип графика, который отображает частоты значений в наборе данных с помощью сложенных точек.
Часто, когда мы создаем точечный график, нас интересует количественная оценка центра и разброса:
- Центр : центральная точка набора данных. Мы часто используем медиану, чтобы измерить это.
- Распространение : распространение значений в наборе данных. Мы часто используем диапазон, чтобы измерить это.
Зная только эти два значения, мы можем получить хорошее представление о том, как значения распределяются в данном наборе данных.
В следующих примерах показано, как на практике найти центр и распространение точечной диаграммы.
Пример 1: Точечный график совершенных фолов
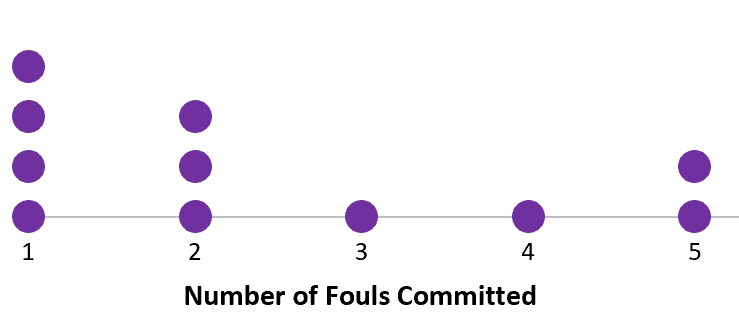
На следующем точечном графике показано количество фолов, совершенных баскетболистами в определенной игре:
Вот как найти центр и разброс значений в этом наборе данных:
Центр : мы можем использовать медиану для измерения «центра» набора данных. Медиана представляет среднее значение набора данных. Чтобы найти медиану для этого конкретного набора данных, мы можем перечислить каждое значение и определить среднее значение:
Значения данных: 1, 1, 1, 1, 2, 2 , 2, 3, 4, 5, 5
Среднее значение в этом наборе данных равно 2 .
Распространение : мы можем использовать диапазон для измерения «разброса» значений в наборе данных. Диапазон представляет собой разницу между наибольшим и наименьшим значением.
В этом наборе данных мы видим, что наибольшее значение равно 5, а наименьшее значение равно 1, поэтому диапазон можно рассчитать как 5 – 1 = 4 .
Пример 2: Точечный график тестовых результатов
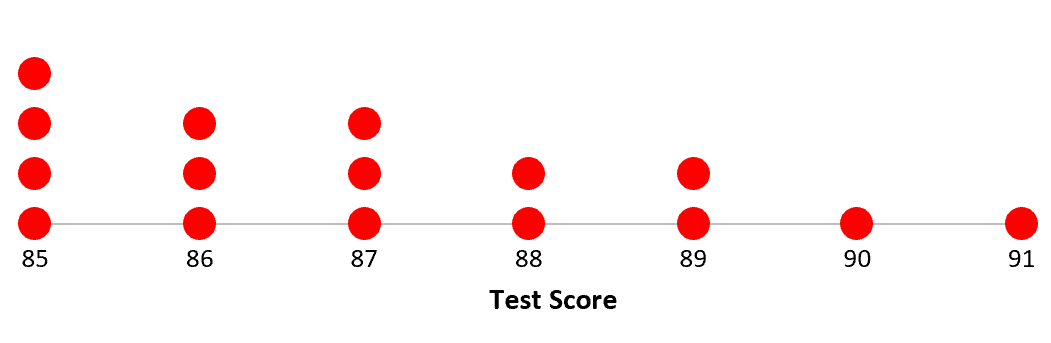
На следующем точечном графике показаны результаты тестов учащихся определенного класса:
Вот как найти центр и разброс значений в этом наборе данных:
Центр : мы можем использовать медиану для измерения «центра» набора данных. Чтобы найти медиану для этого конкретного набора данных, мы можем перечислить каждое значение и определить среднее значение:
Значения данных: 85, 85, 85, 85, 86, 86, 86, 87 , 87 , 87, 88, 88, 89, 89, 90, 91
Этот набор данных имеет четное количество значений, поэтому медиана будет средним значением двух средних значений. Медиана оказывается равной 87 .
Распространение : мы можем использовать диапазон для измерения «разброса» значений в наборе данных, который представляет собой разницу между наибольшим и наименьшим значением.
В этом наборе данных мы видим, что наибольшее значение равно 91, а наименьшее — 85, поэтому диапазон можно рассчитать как 91 — 85 = 6 .
Дополнительные ресурсы
В следующих руководствах объясняется, как создавать точечные диаграммы в различных статистических программах:
Как создать точечный график в Excel
Как создать точечный график в R