Центральная предельная теорема утверждает, что выборочное распределение среднего значения выборки приблизительно нормально, если размер выборки достаточно велик, даже если распределение населения не является нормальным .
Центральная предельная теорема также утверждает, что выборочное распределение будет иметь следующие свойства:
1. Среднее значение выборочного распределения будет равно среднему значению распределения генеральной совокупности:
х = μ
2. Дисперсия выборочного распределения будет равна дисперсии распределения генеральной совокупности, деленной на объем выборки:
с 2 = σ 2 / п
Примеры центральной предельной теоремы
Вот несколько примеров, иллюстрирующих центральную предельную теорему на практике.
Равномерное распределение
Предположим, что ширина панциря черепахи равномерно распределена с минимальной шириной 2 дюйма и максимальной шириной 6 дюймов. То есть, если мы случайным образом выберем черепаху и измерим ширину ее панциря, с одинаковой вероятностью это будет любая ширина от 2 до 6 дюймов.
Если бы мы построили гистограмму, представляющую распределение ширины панциря черепах, она выглядела бы так:

Среднее значение равномерного распределения равно μ = (b+a)/2, где b — максимально возможное значение, а a — наименьшее возможное значение. В данном случае это (6+2)/2=4.
Дисперсия равномерного распределения равна σ 2 = (ba) 2 / 12. В данном случае это (6-2) 2 / 12 = 1,33 .
Взятие случайных выборок из 2 из равномерного распределения
Теперь представьте, что мы берем случайную выборку из двух черепах из этой популяции и измеряем ширину панциря каждой черепахи. Предположим, что панцирь первой черепахи имеет ширину 3 дюйма, а второй — 6 дюймов. Средняя ширина этого образца из двух черепах составляет 4,5 дюйма.
Затем представьте, что мы берем еще одну случайную выборку из двух черепах из этой популяции и снова измеряем ширину панциря каждой черепахи. Предположим, что панцирь первой черепахи имеет ширину 2,5 дюйма, а ширина второй — 2,5 дюйма. Средняя ширина этого образца из двух черепах составляет 2,5 дюйма.
Представьте, что мы снова и снова берем случайные образцы двух черепах и каждый раз находим среднюю ширину панциря.
Если бы мы построили гистограмму, представляющую среднюю ширину панциря всех этих образцов двух черепах, она выглядела бы так:
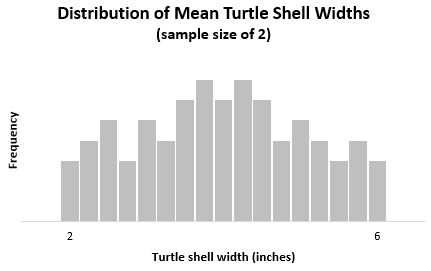
Это известно как распределение выборки для среднего значения выборки, поскольку оно показывает распределение средних значений выборки.
Среднее значение этого выборочного распределения равно x = μ = 4 .
Дисперсия этого выборочного распределения составляет s 2 = σ 2 / n = 1,33 / 2 = 0,665.
Взятие случайных выборок из 5 из равномерного распределения
Теперь представьте, что мы повторили тот же эксперимент, но на этот раз мы снова и снова берем случайные выборки из 5 черепах и каждый раз находим среднюю ширину панциря.
Если бы мы построили гистограмму, представляющую среднюю ширину панциря всех этих выборок из 5 черепах, она выглядела бы так:
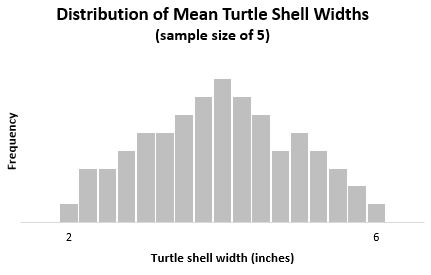
Обратите внимание, что это распределение имеет форму «колокола», напоминающую нормальное распределение.Это связано с тем, что когда мы берем выборки из 5, дисперсия среди наших выборочных средних значений намного ниже, поэтому мы с меньшей вероятностью получим выборки, в которых среднее значение близко к 2 дюймам или близко к 6 дюймам, и с большей вероятностью получим выборки, в которых среднее значение близко к 2 или 6 дюймам. среднее значение ближе к истинному среднему значению населения в 4 дюйма.
Среднее значение этого выборочного распределения равно x = μ = 4 .
Дисперсия этого выборочного распределения составляет s 2 = σ 2 / n = 1,33 / 5 = 0,266.
Взятие случайных выборок из 30 из равномерного распределения
Теперь представьте, что мы повторили тот же эксперимент, но на этот раз мы снова и снова берем случайные выборки из 30 черепах и каждый раз находим среднюю ширину панциря.
Если бы мы построили гистограмму, представляющую среднюю ширину панциря всех этих выборок из 30 черепах, она выглядела бы так:
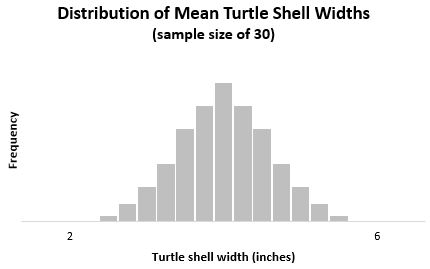
Обратите внимание, что это распределение выборки имеет еще более колоколообразную форму и намного уже, чем два предыдущих распределения.
Среднее значение этого выборочного распределения равно x = μ = 4 .
Дисперсия этого выборочного распределения составляет s 2 = σ 2 / n = 1,33 / 30 = 0,044.
Распределение хи-квадрат
Предположим, что количество домашних животных на семью в определенном городе следует распределению хи-квадрат с тремя степенями свободы. Если бы мы построили гистограмму распределения домашних животных по семьям, она выглядела бы так:
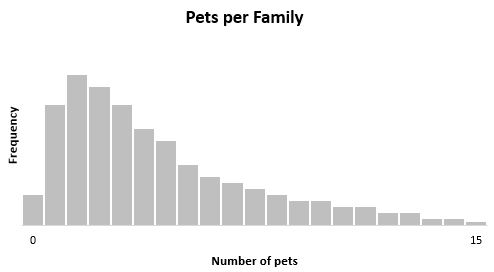
Среднее значение распределения хи-квадрат — это просто число степеней свободы(df). В этом случае µ = 3 .
Дисперсия распределения хи-квадрат равна 2 * df.В этом случае σ 2 = 2 * 3 = 6 .
Взятие случайных выборок из 2
Представьте, что мы берем случайную выборку из 2 семей из этой популяции и подсчитываем количество домашних животных в каждой семье. Предположим, что в первой семье 4 питомца, а во второй — 1 питомец. Среднее количество домашних животных для этой выборки из 2 семей составляет 2,5.
Затем представьте, что мы берем еще одну случайную выборку из 2 семей из этой совокупности и снова подсчитываем количество домашних животных в каждой семье. Предположим, что в первой семье 6 домашних животных, а во второй семье 4 домашних животных. Среднее количество домашних животных для этой выборки из 2 семей равно 5.
Представьте, что мы снова и снова берем случайные выборки из двух семей и каждый раз находим среднее количество домашних животных.
Если бы мы построили гистограмму для представления среднего количества домашних животных во всех этих выборках из 2 семей, она выглядела бы так:
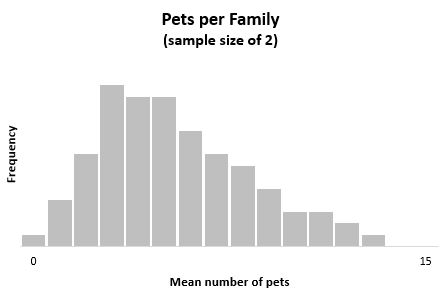
Среднее значение этого выборочного распределения равно x = μ = 3 .
Дисперсия этого выборочного распределения равна s 2 = σ 2 / n = 6 / 2 = 3 .
Взятие случайных выборок из 10
Теперь представьте, что мы повторили тот же эксперимент, но на этот раз мы снова и снова берем случайные выборки из 10 семей и каждый раз находим среднее количество домашних животных в семье.
Если бы мы построили гистограмму, представляющую среднее количество домашних животных на семью во всех этих выборках из 10 семей, она выглядела бы так:
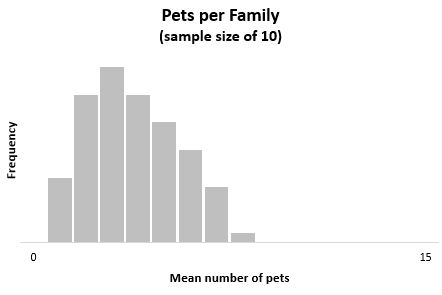
Среднее значение этого выборочного распределения равно x = μ = 3 .
Дисперсия этого выборочного распределения составляет s 2 = σ 2 / n = 6 / 10 = 0,6 .
Взятие случайных выборок из 30
Теперь представьте, что мы повторили тот же эксперимент, но на этот раз мы снова и снова берем случайные выборки из 30 семей и каждый раз находим среднее количество домашних животных в семье.
Если бы мы построили гистограмму, представляющую среднее количество домашних животных на семью во всех этих выборках из 30 семей, она выглядела бы так:
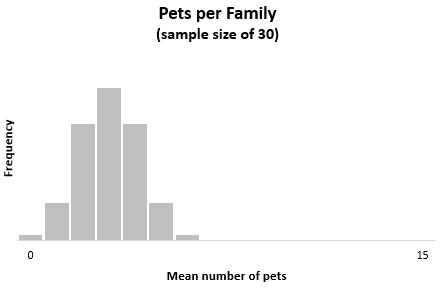
Среднее значение этого выборочного распределения равно x = μ = 3 .
Дисперсия этого выборочного распределения составляет s 2 = σ 2 / n = 6 / 30 = 0,2 .
Резюме
Вот основные выводы из этих двух примеров:
- Выборочное распределение выборочного среднего является приблизительно нормальным, если размер выборки достаточно велик, даже если распределение генеральной совокупности не является нормальным.В двух приведенных выше примерах ни равномерное распределение, ни распределение хи-квадрат не были нормальными (они вообще не имели формы «колокола»), но когда мы взяли достаточно большой размер выборки, распределение выборочного среднего стало выходит быть нормальным.
- Чем больше размер выборки, тем меньше дисперсия выборочного среднего.
Определение «достаточно большой»
Напомним, что центральная предельная теорема утверждает, что выборочное распределение среднего значения выборки приблизительно нормально, если размер выборки «достаточно велик» , даже если распределение генеральной совокупности не является нормальным.
Нет точного определения того, насколько большим должен быть размер выборки, чтобы можно было применить центральную предельную теорему, но в целом это зависит от асимметрии распределения населения, из которого взята выборка:
- Если распределение населения симметрично, иногда достаточно размера выборки всего 15 человек.
- Если распределение населения асимметрично, обычно требуется размер выборки не менее 30 человек.
- Если распределение населения крайне асимметрично, может потребоваться размер выборки 40 или более человек.
Ознакомьтесь с этим учебным пособием по условиям большой выборки для получения дополнительной информации по этой теме.


