Коэффициент вариации , часто обозначаемый как CV, представляет собой способ измерения степени разброса значений в наборе данных по отношению к среднему значению. Он рассчитывается как:
CV = σ / μ
куда:
σ = стандартное отклонение набора данных
μ = среднее значение набора данных
Проще говоря, коэффициент вариации — это просто отношение между стандартным отклонением и средним значением.
Когда используется коэффициент вариации?
Коэффициент вариации часто используется для сравнения вариации между двумя разными наборами данных.
В реальном мире он часто используется в финансах для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций. Это позволяет инвесторам сравнивать соотношение риска и доходности между инвестициями.
Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:
Взаимный фонд A: среднее = 7%, стандартное отклонение = 12,4%
Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%
При расчете коэффициента вариации для каждого фонда инвестор находит:
CV для взаимного фонда A = 12,4% / 7% = 1,77
CV для взаимного фонда B = 8,2% / 5% = 1,64
Поскольку взаимный фонд B имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.
Как рассчитать коэффициент вариации в Excel
В Excel нет встроенной формулы для расчета коэффициента вариации для набора данных, но, к счастью, его относительно легко вычислить, используя пару простых формул. В следующем примере показано, как рассчитать коэффициент вариации для заданного набора данных.
Предположим, у нас есть следующий набор данных, содержащий экзаменационные оценки 20 студентов:
Чтобы рассчитать коэффициент вариации для этого набора данных, нам нужно знать только два числа: среднее значение и стандартное отклонение. Их можно рассчитать по следующим формулам:
Среднее значение: =СРЕДНЕЕ(A2:A21)
Стандартное отклонение: =СТАНДОТКЛОН(A2:A21)
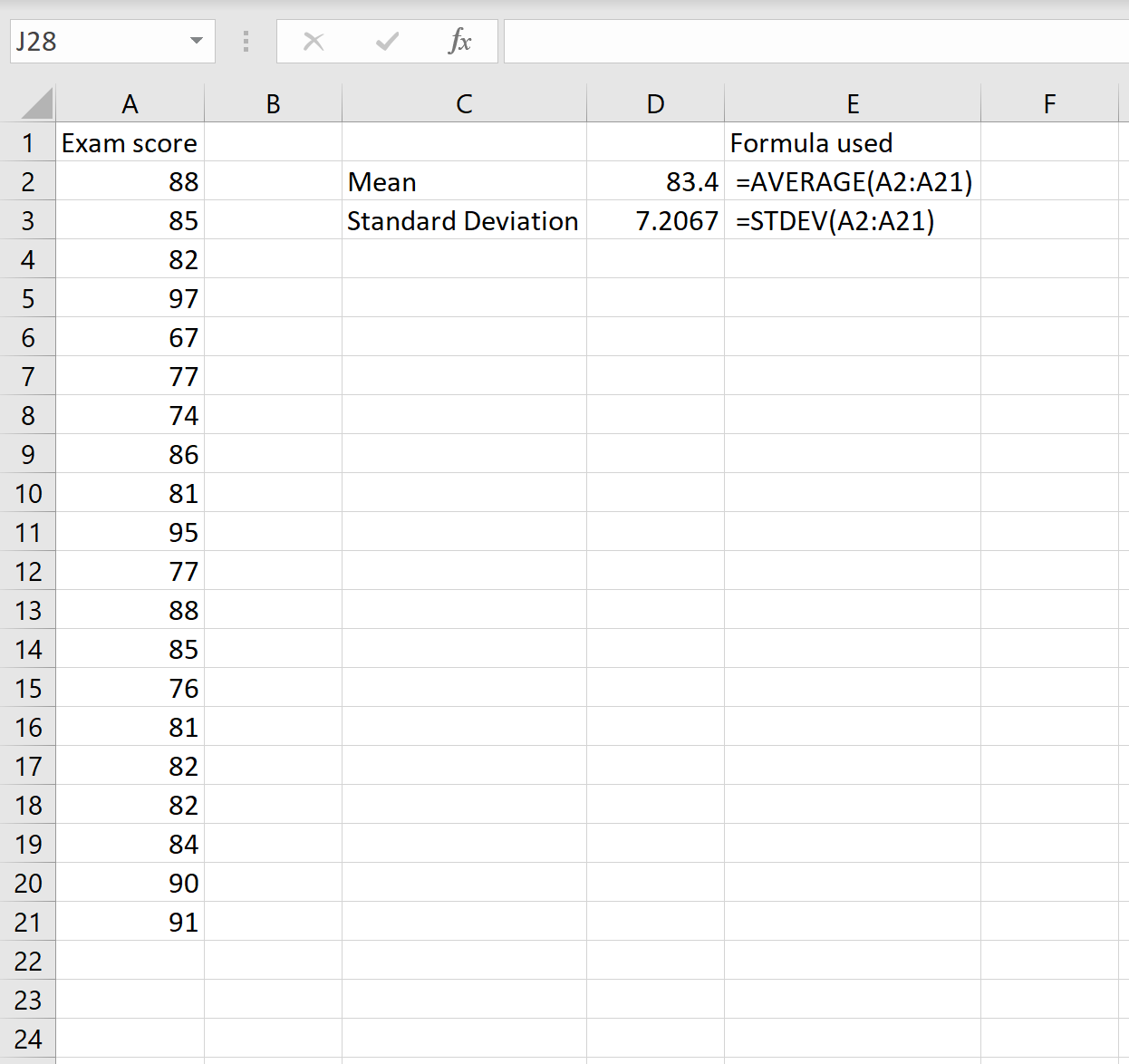
Чтобы вычислить коэффициент вариации, мы затем делим стандартное отклонение на среднее значение:
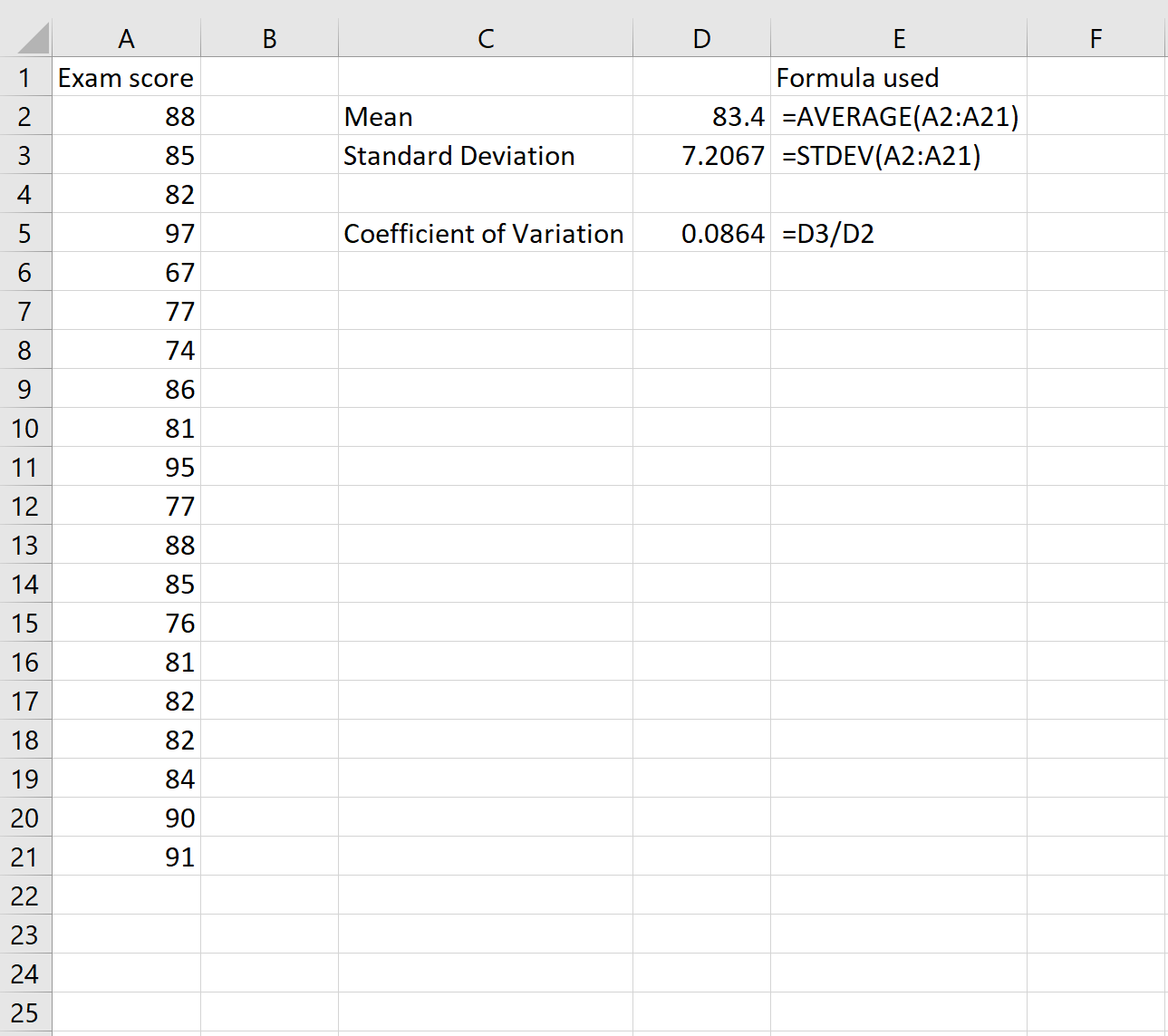
Коэффициент вариации оказывается равным 0,0864 .
Обратите внимание, что мы также могли бы использовать только одну формулу для расчета CV:
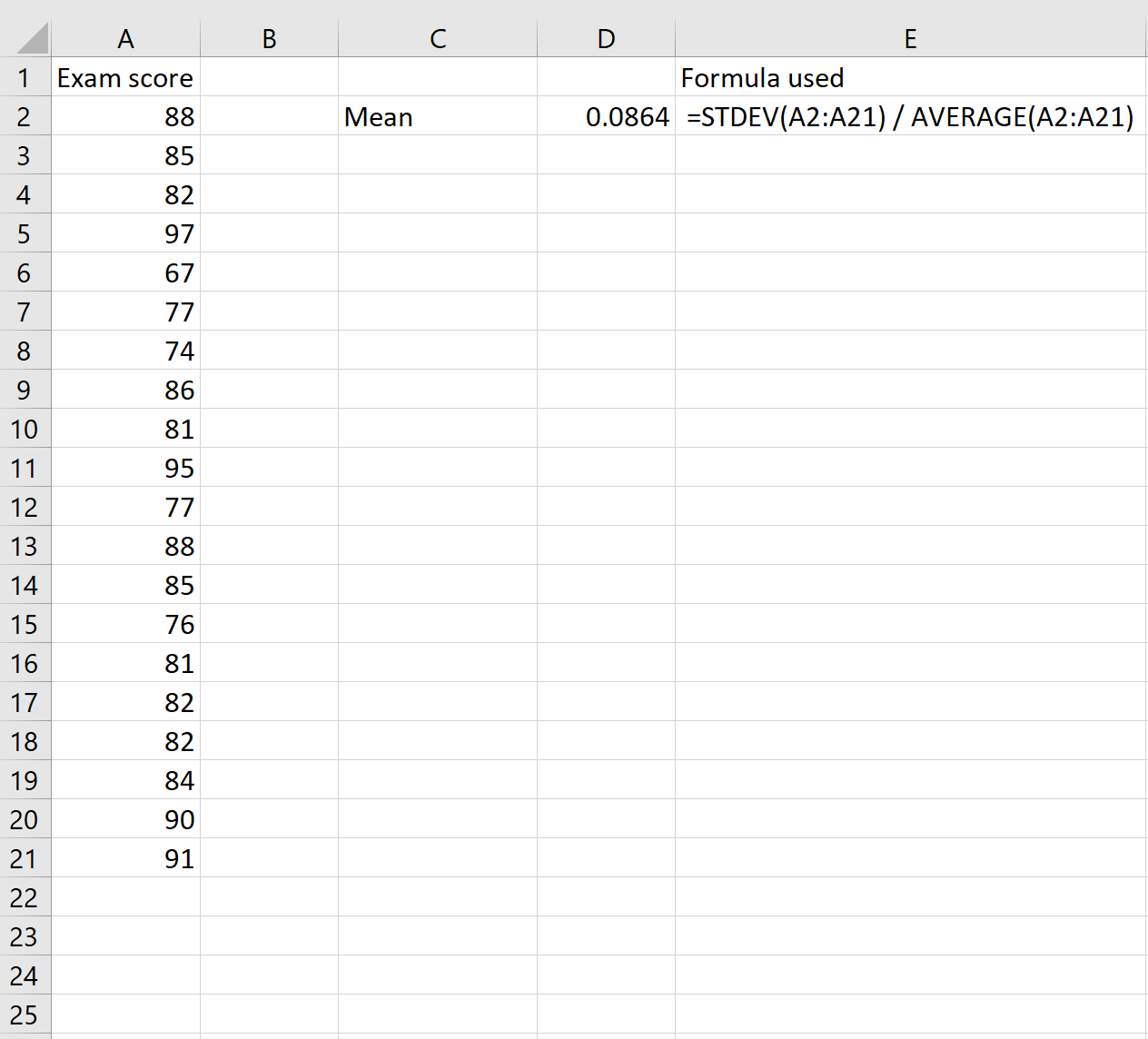
Это приводит к тому же CV 0,0864 .