Z-оценка показывает, на сколько стандартных отклонений отдельное значение данных отпадает от среднего значения. Он рассчитывается как:
z-оценка = (x – μ) / σ
куда:
- x: индивидуальное значение данных
- μ: среднее значение населения
- σ: стандартное отклонение населения
Z-показатель для отдельного значения можно интерпретировать следующим образом:
- Положительный z-показатель: отдельное значение больше среднего.
- Отрицательный z-показатель: отдельное значение меньше среднего.
- Z-показатель 0: индивидуальное значение равно среднему.
Z-оценки особенно полезны, когда мы хотим сравнить относительное положение двух точек данных из двух разных распределений. Чтобы проиллюстрировать это, рассмотрим следующий пример.
Пример: сравнение Z-показателей
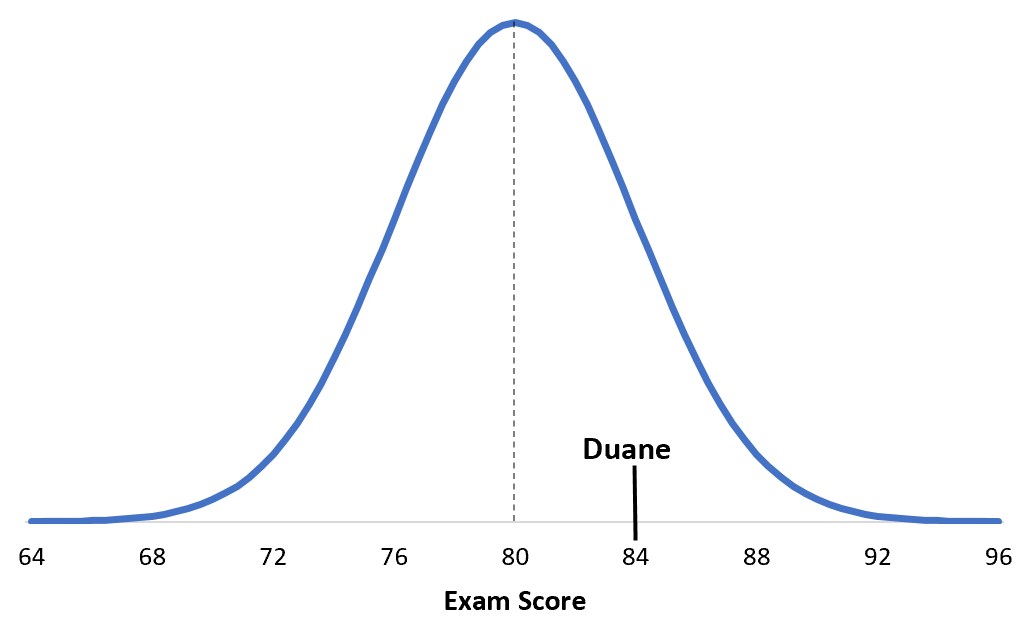
Баллы на определенном экзамене в колледже обычно распределяются со средним значением μ = 80 и стандартным отклонением σ = 4. Дуэйн набирает 84 балла на этом экзамене.
Баллы на другом экзамене в колледже распределяются нормально со средним значением μ = 85 и стандартным отклонением σ = 8. Дебби набирает 90 баллов на этом экзамене.
По сравнению с их собственным распределением баллов за экзамен, кто набрал больше баллов на своем экзамене?
Чтобы ответить на этот вопрос, мы можем рассчитать z-балл экзаменационного балла каждого человека:
Z-показатель Дуэйна = (x - μ) / σ = (84 - 80) / 4 = 4 / 4 = 1
Z-показатель Дебби = (x - μ) / σ = (90 - 85) / 8 = 5 / 8 = 0,625
Хотя Дебби набрала более высокий балл, балл Дуэйна на самом деле выше по сравнению с распределением его конкретного экзамена.
Чтобы понять это, полезно визуализировать ситуацию. Вот оценка экзамена Дуэйна относительно распределения его конкретного экзамена:

А вот экзаменационный балл Дебби по отношению к распределению ее экзамена:
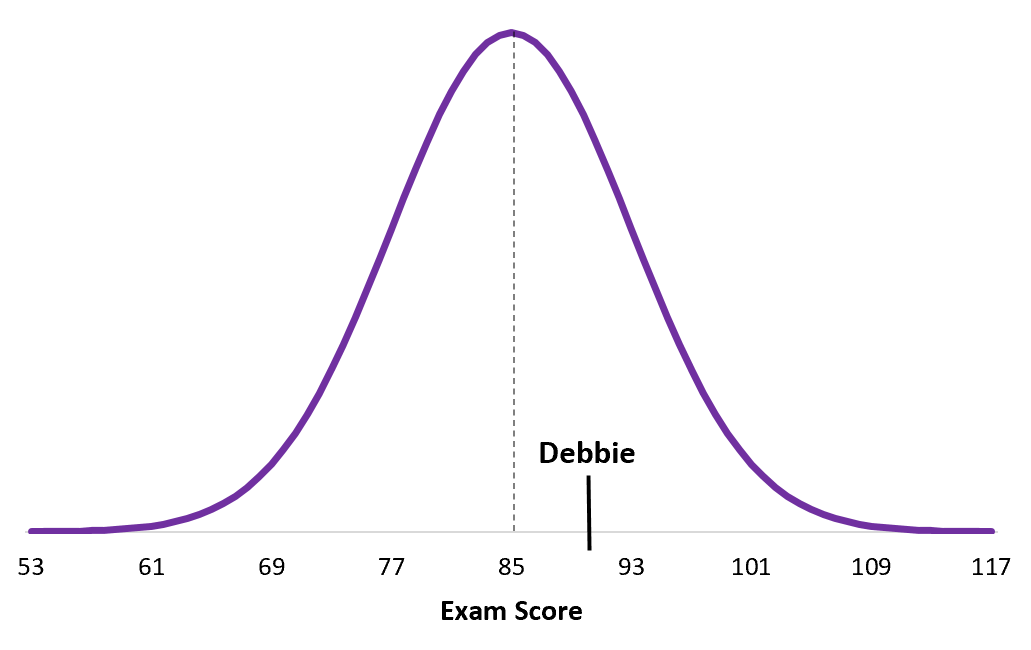
Обратите внимание, как показатель Дебби ближе к ее среднему значению для населения по сравнению с Дуэйном. Хотя в целом у нее более высокий балл, ее z-балл ниже просто потому, что средний балл на ее конкретном экзамене выше.
Этот пример иллюстрирует, почему z-показатели так полезны для сравнения значений данных из разных распределений: z-показатели учитывают среднее значение и стандартное отклонение распределений, что позволяет нам сравнивать значения данных из разных распределений и видеть, какое из них выше относительно свои собственные дистрибутивы.