Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.
Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция распределения X может быть записана как:
F (х; λ) = 1 – e -λx
куда:
- λ: параметр скорости (рассчитывается как λ = 1/μ)
- e: константа, примерно равная 2,718.
В этом руководстве объясняется, как использовать экспоненциальное распределение в Python.
Как сгенерировать экспоненциальное распределение
Вы можете использовать функцию expon.rvs(scale, size) из библиотеки SciPy в Python для генерации случайных значений из экспоненциального распределения с определенным параметром скорости и размером выборки:
from scipy. stats import expon
#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )
array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
34.60922432, 2.68266663, 22.70459831, 97.66661811,
6.64272914, 46.15547298])
Примечание.Полную документацию по библиотеке SciPy можно найти здесь .
Как рассчитать вероятности с помощью экспоненциального распределения
Предположим, что среднее количество минут между извержениями определенного гейзера составляет 40 минут. Какова вероятность того, что нам придется ждать извержения менее 50 минут?
Чтобы решить эту проблему, нам нужно сначала рассчитать параметр скорости:
- λ = 1/мк
- λ = 1/40
- λ = 0,025
Мы можем подставить λ = 0,025 и x = 50 в формулу CDF:
- P(X ≤ x) = 1 – e -λx
- P(X ≤ 50) = 1 – e -0,025(50)
- Р(Х ≤ 50) = 0,7135
Вероятность того, что нам придется ждать следующего извержения менее 50 минут, равна 0,7135 .
Мы можем использовать функцию expon.cdf() из SciPy, чтобы решить эту проблему в Python:
from scipy. stats import expon
#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)
0.7134952031398099
Вероятность того, что нам придется ждать следующего извержения менее 50 минут, равна 0,7135 .
Это соответствует значению, которое мы рассчитали вручную.
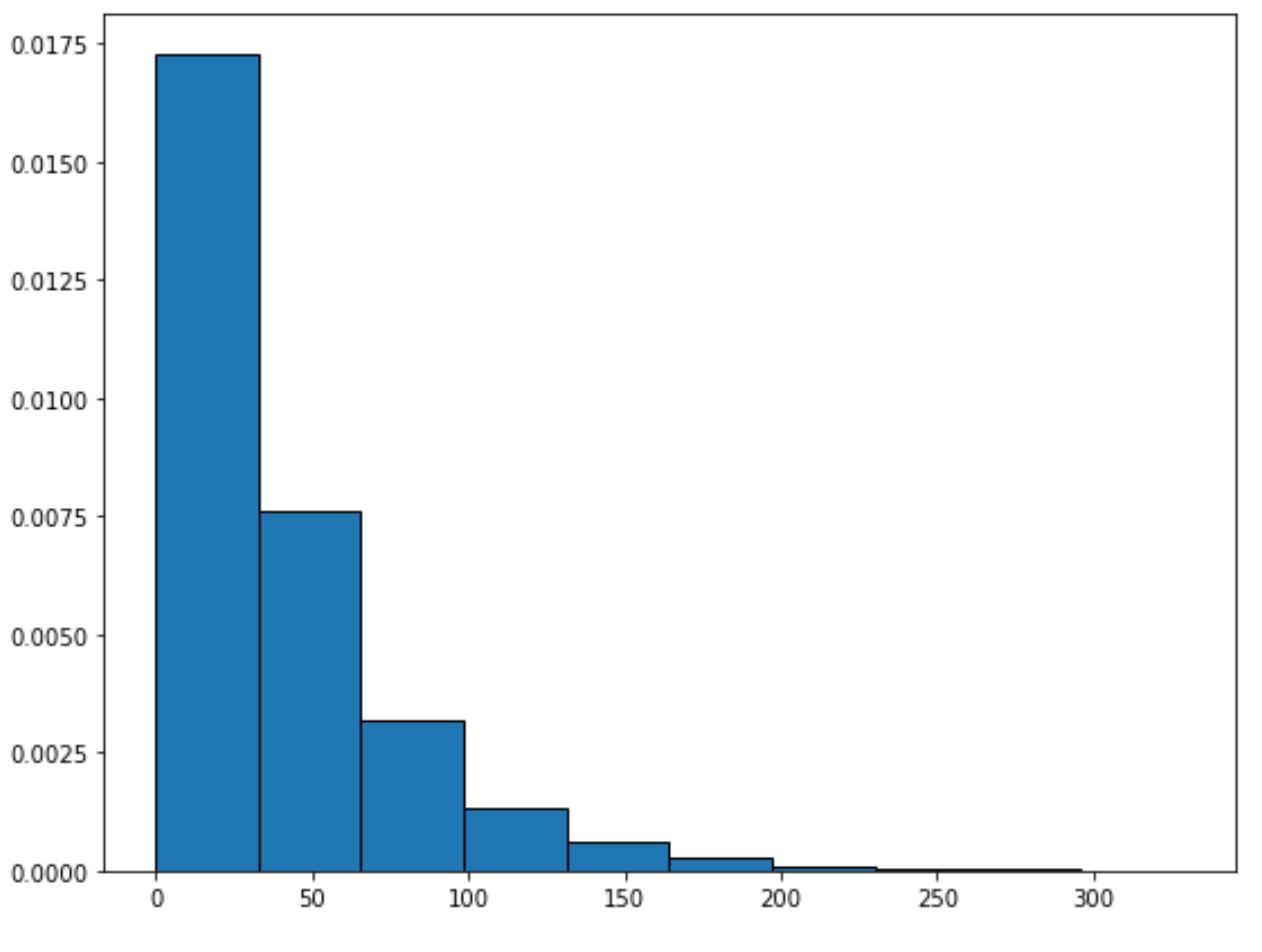
Как построить экспоненциальное распределение
Вы можете использовать следующий синтаксис для построения экспоненциального распределения с заданным параметром скорости:
from scipy. stats import expon
import matplotlib.pyplot as plt
#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 , size= 10000 )
#create plot of exponential distribution
plt.hist (x, density= True , edgecolor='black')
Дополнительные ресурсы
В следующих руководствах объясняется, как использовать другие распространенные дистрибутивы в Python:
Как использовать распределение Пуассона в Python
Как использовать дистрибутив t в Python
Как использовать равномерное распределение в Python