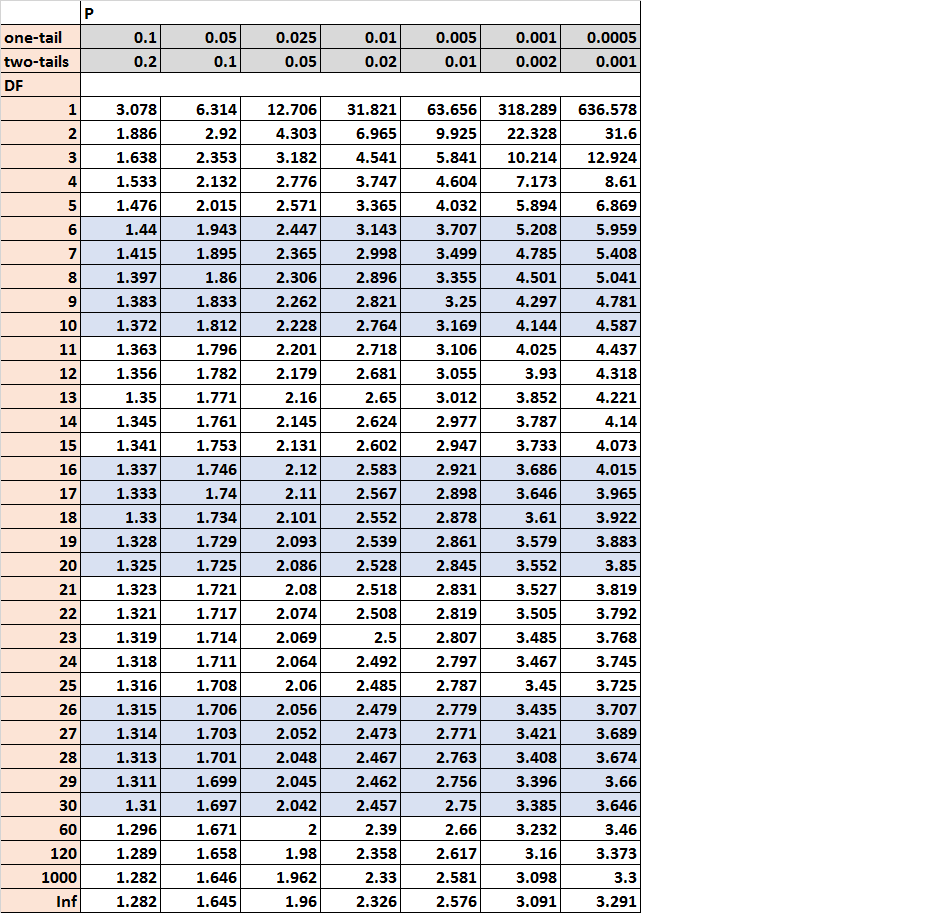
Таблица t-распределения — это таблица, которая показывает критические значения t-распределения. Чтобы использовать таблицу распределения t, вам нужны только три значения:
- Уровень значимости (обычно выбирают 0,01, 0,05 и 0,10).
- Степени свободы
- Тип теста (односторонний или двусторонний)
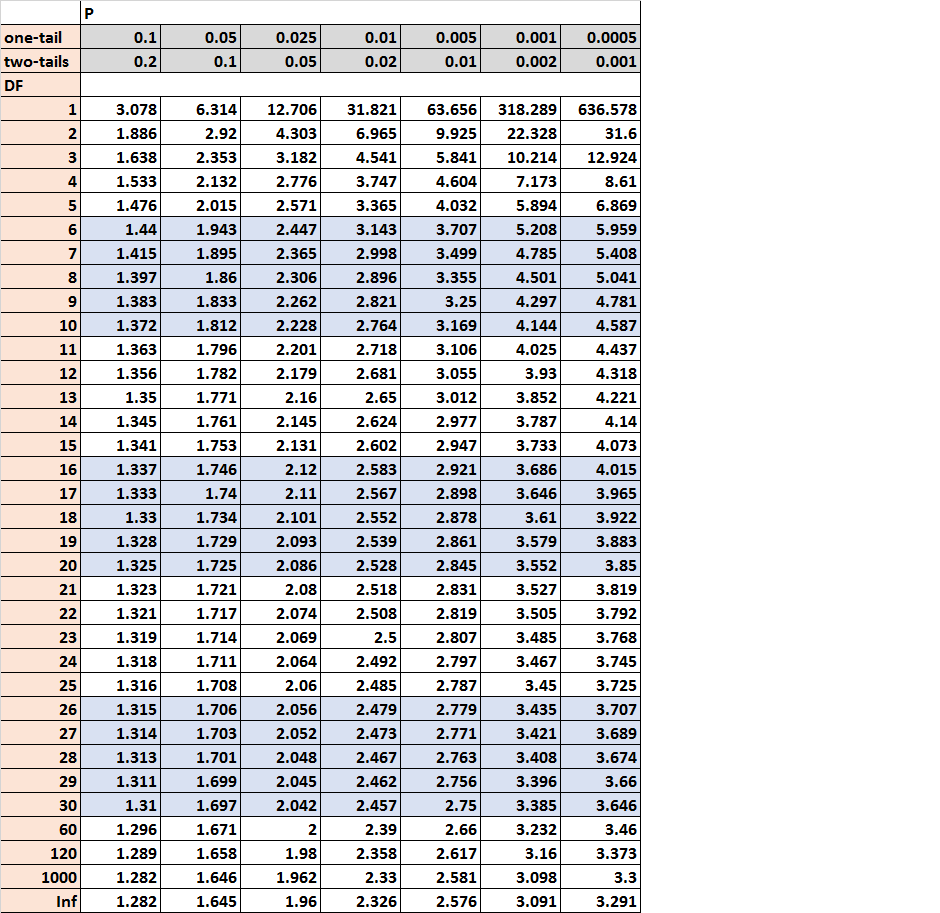
т распределительный стол Таблица распределения t обычно используется в следующих проверках гипотез:
- Проверка гипотезы для среднего
- Проверка гипотезы о разнице в средних
- Проверка гипотезы о разнице в парных средних
Когда вы проведете каждый из этих тестов, вы получите тестовую статистику t.Чтобы узнать, является ли эта тестовая статистика статистически значимой на некотором альфа-уровне, у вас есть два варианта:
- Сравните тестовую статистику t с критическим значением из таблицы распределения t.
- Сравните p-значение тестовой статистики t с выбранным альфа-уровнем.
Давайте рассмотрим пример использования каждого из этих подходов.
Примеры
Предположим, мы проводим двустороннюю проверку гипотезы с альфа-уровнем 0,05 , чтобы выяснить, различается ли средняя потеря веса между двумя диетами. Предположим, что наша тестовая статистика t равна 1,34 , а наши степени свободы равны 22.Мы хотели бы знать, являются ли эти результаты статистически значимыми.
Сравните тестовую статистику t с критическим значением
Первый подход, который мы можем использовать, чтобы определить, являются ли наши результаты статистически значимыми, заключается в сравнении тестовой статистики t , равной 1,34 , с критическим значением в таблице распределения t. Критическое значение — это значение в таблице, которое соответствует двустороннему значению 0,05 и степени свободы 22.Это число оказывается равным 2,074 :

Поскольку статистика нашего теста t ( 1,34 ) меньше критического значения ( 2,074 ), мы не можем отвергнуть нулевую гипотезу нашего теста. У нас нет достаточных доказательств, чтобы сказать, что средняя потеря веса между двумя диетами является статистически значимой при уровне альфа 0,05.
Сравните p-значение с выбранным альфа-уровнем
Второй подход, который мы можем использовать, чтобы определить, являются ли наши результаты статистически значимыми, состоит в том, чтобы найти p-значение для тестовой статистики t , равной 1,34.Чтобы найти это p-значение, мы не можем использовать таблицу распределения t, потому что она предоставляет нам только критические значения, а не p-значения .
Итак, чтобы найти это значение p, нам нужно использовать калькулятор T Score to P Value со следующими входными данными:


Значение p для тестовой статистики t , равной 1,34 , для двустороннего теста с 22 степенями свободы равно 0,19392.Поскольку это число больше, чем наш альфа-уровень 0,05 , мы не можем отвергнуть нулевую гипотезу нашего теста. У нас нет достаточных доказательств, чтобы сказать, что средняя потеря веса между двумя диетами является статистически значимой при уровне альфа 0,05.
Когда использовать таблицу распределения t
Если вас интересует нахождение критического значения t для заданного уровня значимости, степеней свободы и типа теста (односторонний или двусторонний), то вам следует использовать таблицу распределения t .
Вместо этого, если у вас есть заданная тестовая статистика t и вы просто хотите узнать p-значение этой тестовой статистики, вам нужно будет использовать калькулятор T Score to P Value Calculator для этого.