Иерархическая регрессия — это метод, который мы можем использовать для сравнения нескольких различных линейных моделей.
Основная идея состоит в том, что сначала мы подбираем модель линейной регрессии только с одной независимой переменной. Затем мы подгоняем другую модель регрессии, используя дополнительную объясняющую переменную. Если R-квадрат (доля дисперсии переменной отклика, которая может быть объяснена независимыми переменными) во второй модели значительно выше, чем R-квадрат в предыдущей модели, это означает, что вторая модель лучше.
Затем мы повторяем процесс подбора дополнительных регрессионных моделей с дополнительными объясняющими переменными и смотрим, предлагают ли новые модели какие-либо улучшения по сравнению с предыдущими моделями.
В этом руководстве представлен пример выполнения иерархической регрессии в Stata.
Пример: иерархическая регрессия в Stata
Мы будем использовать встроенный набор данных с именем auto , чтобы проиллюстрировать, как выполнять иерархическую регрессию в Stata. Сначала загрузите набор данных, введя следующее в поле «Команда»:
сисус авто
Мы можем получить краткую сводку данных, используя следующую команду:
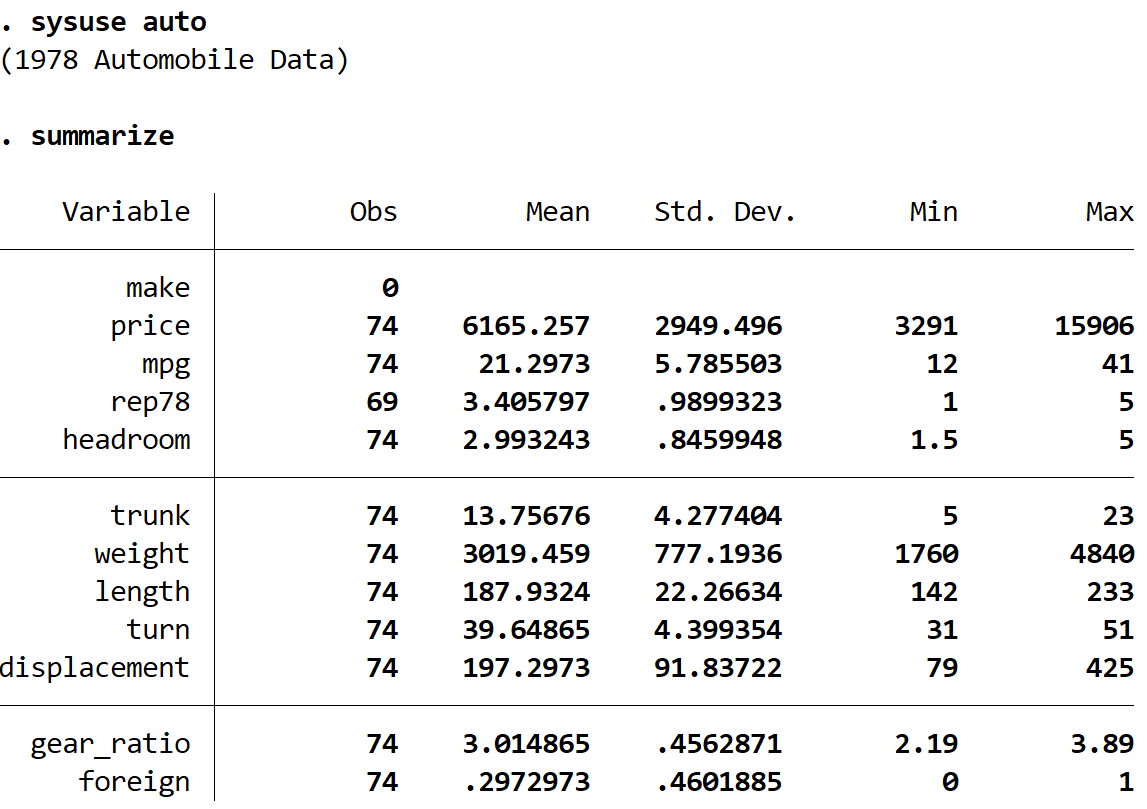
подвести итог

Мы видим, что набор данных содержит информацию о 12 различных переменных для 74 автомобилей.
Мы подберем следующие три модели линейной регрессии и используем иерархическую регрессию, чтобы увидеть, обеспечивает ли каждая последующая модель значительное улучшение предыдущей модели или нет:
Модель 1: цена = перехват + миль на галлон
Модель 2: цена = перехват + миль на галлон + вес
Модель 3: цена = перехват + мили на галлон + вес + передаточное число
Чтобы выполнить иерархическую регрессию в Stata, нам сначала нужно установить пакет Hireg.Для этого введите в поле Command следующее:
найди наймарег
В появившемся окне нажмите на найм с http://fmwww.bc.edu/RePEc/bocode/h.
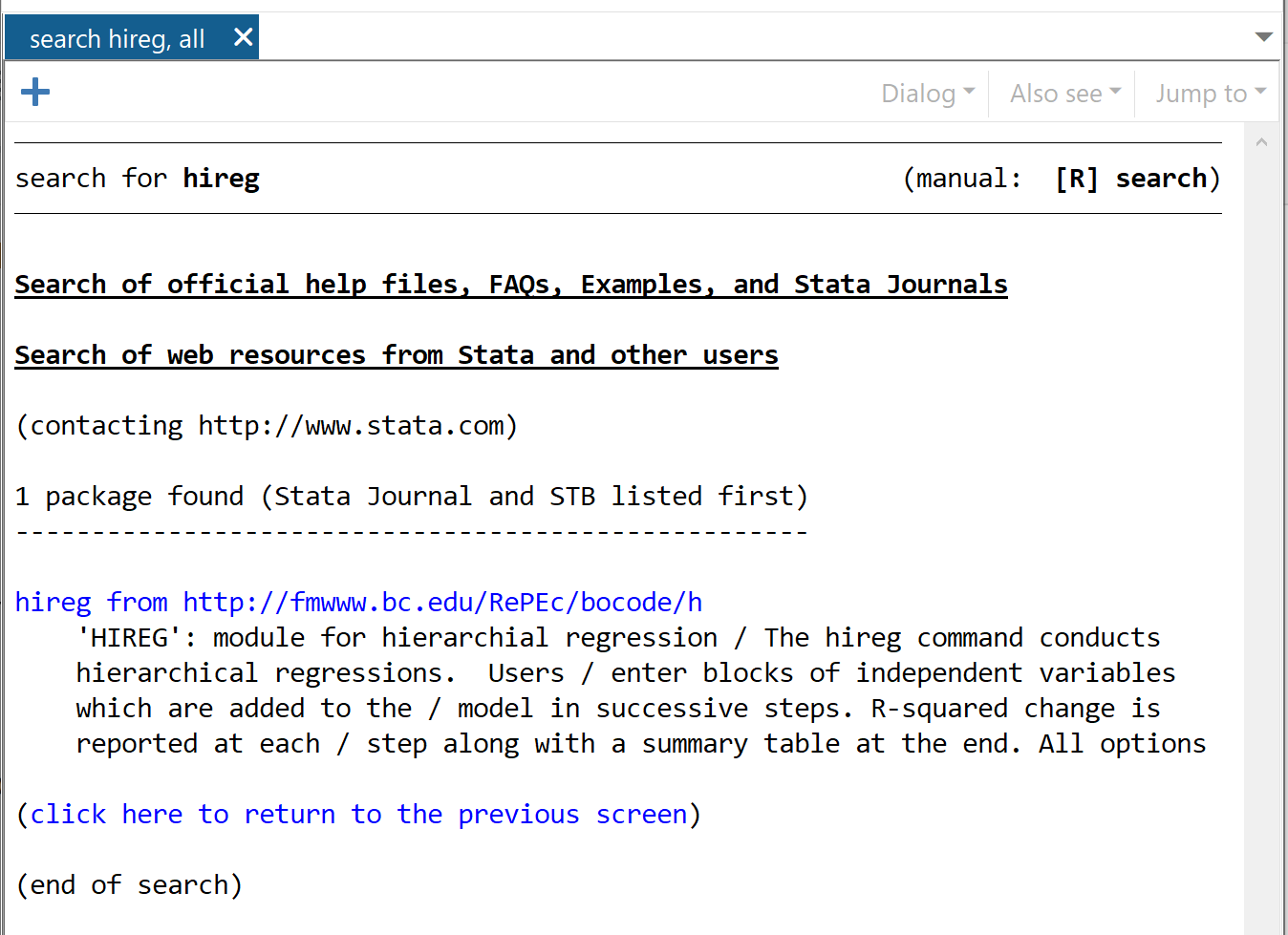
В следующем окне щелкните ссылку с надписью « Нажмите здесь, чтобы установить» .

Пакет будет установлен за считанные секунды. Далее, для выполнения иерархической регрессии мы будем использовать следующую команду:
цена аренды (миль на галлон) (вес) (gear_ratio)
Вот что это говорит Stata делать:
- Выполните иерархическую регрессию, используя цену в качестве переменной отклика в каждой модели.
- Для первой модели используйте mpg в качестве независимой переменной.
- Для второй модели добавьте вес в качестве дополнительной независимой переменной.
- Для третьей модели добавьте gear_ratio в качестве еще одной независимой переменной.
Вот результат первой модели:
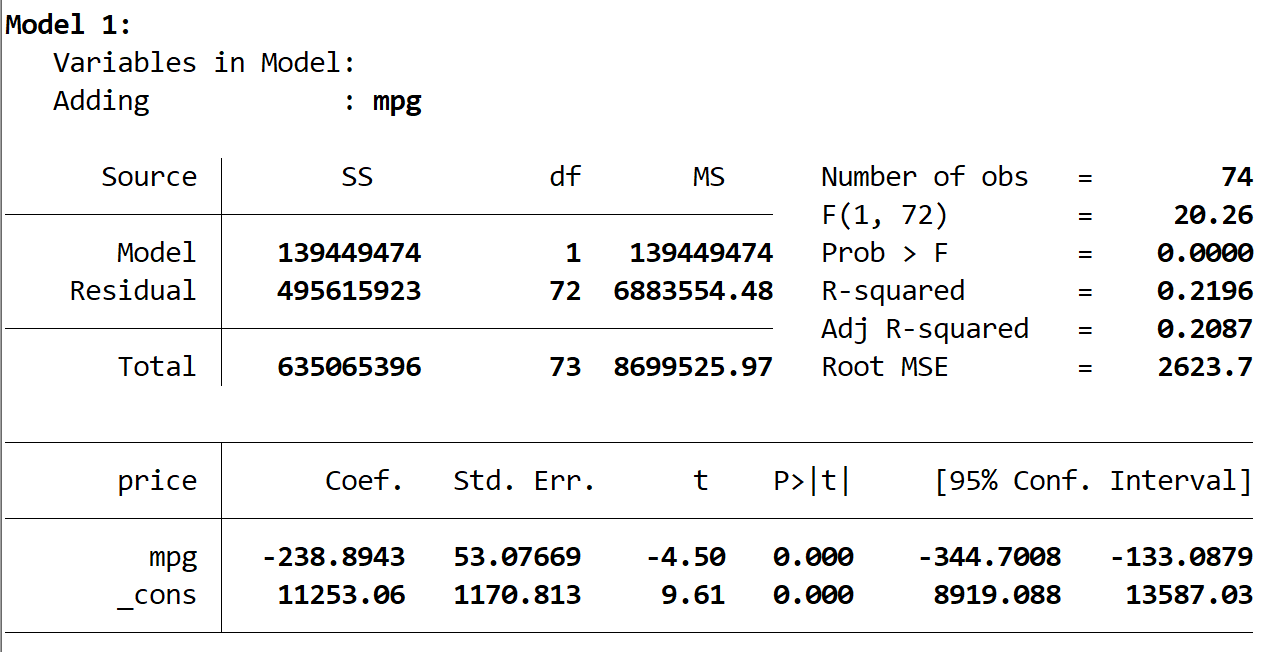
Мы видим, что R-квадрат модели равен 0,2196 , а общее p-значение (Prob > F) для модели равно 0,0000 , что является статистически значимым при α = 0,05.
Далее мы видим вывод второй модели:

R-квадрат этой модели равен 0,2934 , что больше, чем у первой модели. Чтобы определить, является ли эта разница статистически значимой, Stata провела F-тест, в результате которого в нижней части вывода были получены следующие числа:
- Разница R-квадрата между двумя моделями = 0,074.
- F-статистика для разницы = 7,416
- Соответствующее значение p F-статистики = 0,008 .
Поскольку p-значение меньше 0,05, мы делаем вывод о статистически значимом улучшении второй модели по сравнению с первой моделью.
Наконец, мы можем увидеть результат третьей модели:
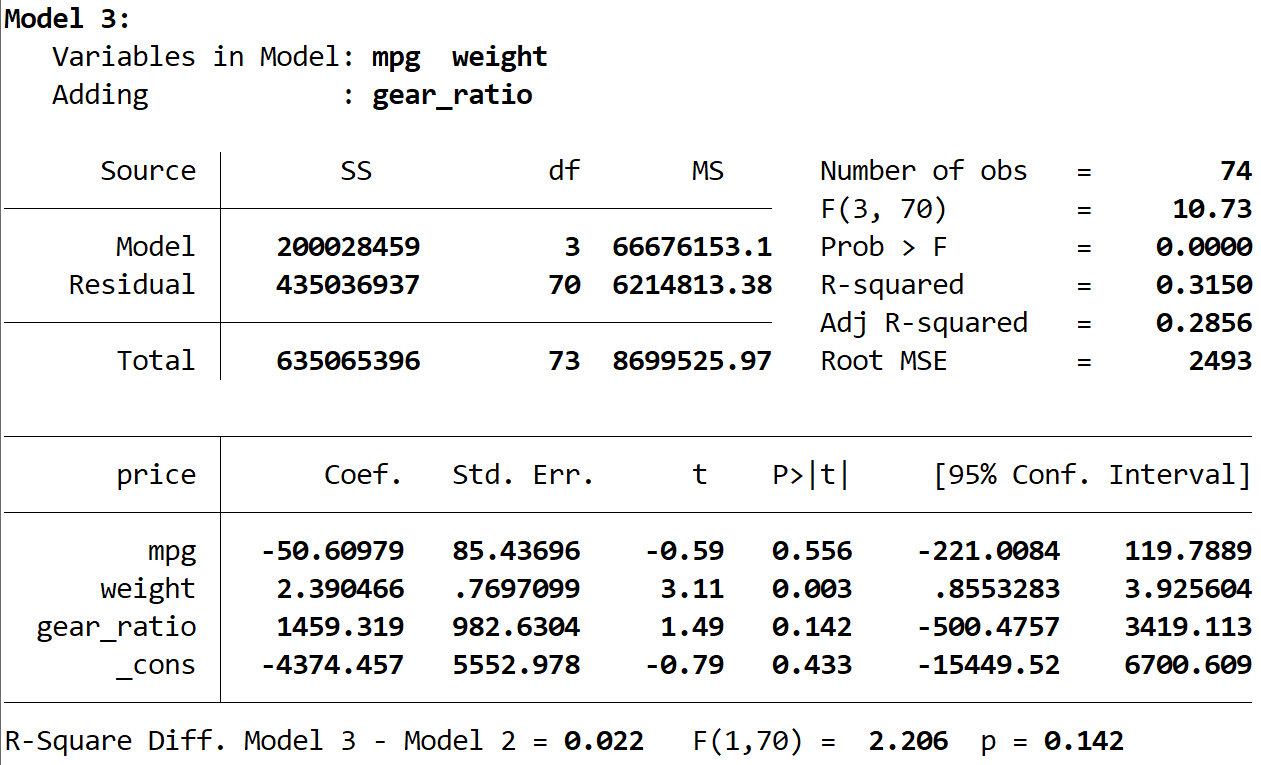
R-квадрат этой модели равен 0,3150 , что больше, чем у второй модели. Чтобы определить, является ли эта разница статистически значимой, Stata провела F-тест, в результате которого в нижней части вывода были получены следующие числа:
- Разница R-квадрата между двумя моделями = 0,022 .
- F-статистика для разницы = 2,206
- Соответствующее значение p F-статистики = 0,142.
Поскольку p-значение не меньше 0,05, у нас нет достаточных доказательств, чтобы сказать, что третья модель предлагает какое-либо улучшение по сравнению со второй моделью.
В самом конце вывода мы видим, что Stata предоставляет сводку результатов:

В этом конкретном примере мы бы пришли к выводу, что модель 2 предлагает значительное улучшение по сравнению с моделью 1, но модель 3 не предлагает значительного улучшения по сравнению с моделью 2.