Двухфакторный дисперсионный анализ используется, чтобы определить, есть ли разница между средними значениями трех или более независимых групп, которые были разделены на два фактора.
Мы используем двусторонний дисперсионный анализ, когда хотим узнать, влияют ли два конкретных фактора на определенную переменную отклика. Однако иногда между двумя факторами присутствует эффект взаимодействия , который может повлиять на то, как мы интерпретируем взаимосвязь между факторами и переменной отклика.
Например, мы можем захотеть узнать, влияют ли факторы (1) физические упражнения и (2) пол на переменную реакции на потерю веса.Хотя возможно, что оба фактора влияют на потерю веса, также возможно, что эти два фактора взаимодействуют друг с другом.
Например, возможно, что физические упражнения приводят к потере веса с разной скоростью у мужчин и женщин. В этом случае существует эффект взаимодействия между физическими упражнениями и полом.
Самый простой способ обнаружить и понять эффекты взаимодействия между двумя факторами — это построить график взаимодействия .
Это тип графика, который отображает подогнанные значения переменной отклика по оси Y и значения первого фактора по оси X. Между тем линии на графике представляют значения второго интересующего фактора.
В этом руководстве объясняется, как создать и интерпретировать график взаимодействия в R.
Пример: График взаимодействия в R
Предположим, исследователи хотят определить, влияют ли интенсивность упражнений и пол на потерю веса. Чтобы проверить это, они набирают 30 мужчин и 30 женщин для участия в эксперименте, в котором они случайным образом распределяют по 10 человек для выполнения программы либо без упражнений, либо с легкими, либо с интенсивными упражнениями в течение одного месяца.
Используйте следующие шаги, чтобы создать фрейм данных в R, выполнить двусторонний ANOVA и создать график взаимодействия, чтобы визуализировать эффект взаимодействия между физическими упражнениями и полом.
Шаг 1: Создайте данные.
Следующий код показывает, как создать фрейм данных в R:
#make this example reproducible
set.seed(10)
#create data frame
data <- data.frame(gender = rep (c("Male", "Female"), each = 30 ),
exercise = rep (c("None", "Light", "Intense"), each = 10 , times = 2 ),
weight_loss = c(runif(10, -3, 3), runif(10, 0, 5), runif(10, 5, 9),
runif(10, -4, 2), runif(10, 0, 3), runif(10, 3, 8)))
#view first six rows of data frame
head(data)
gender exercise weight_loss
1 Male None 0.04486922
2 Male None -1.15938896
3 Male None -0.43855400
4 Male None 1.15861249
5 Male None -2.48918419
6 Male None -1.64738030
Шаг 2: Установите двухфакторную модель ANOVA.
В следующем коде показано, как применить двухфакторный дисперсионный анализ к данным:
#fit the two-way ANOVA model
model <- aov(weight_loss ~ gender \* exercise, data = data)
#view the model output
summary(model)
# Df Sum Sq Mean Sq F value Pr(>F)
#gender 1 15.8 15.80 11.197 0.0015 \*\*
#exercise 2 505.6 252.78 179.087 <2e-16 \*\*\*
#gender:exercise 2 13.0 6.51 4.615 0.0141 \*
#Residuals 54 76.2 1.41
#---
#Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Обратите внимание, что значение p ( 0,0141 ) для термина взаимодействия между физическими упражнениями и полом является статистически значимым, что указывает на наличие значительного эффекта взаимодействия между двумя факторами.
Шаг 3: Создайте график взаимодействия.
В следующем коде показано, как создать график взаимодействия для упражнений и пола:
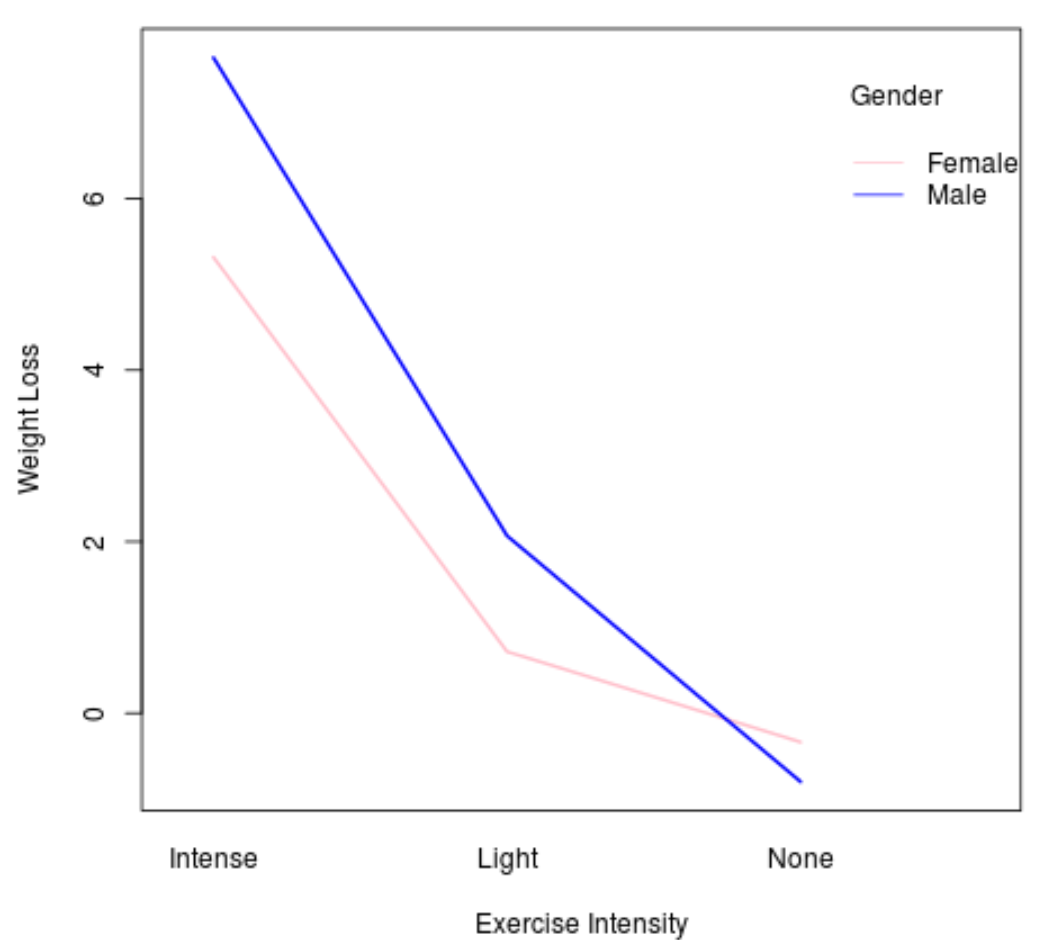
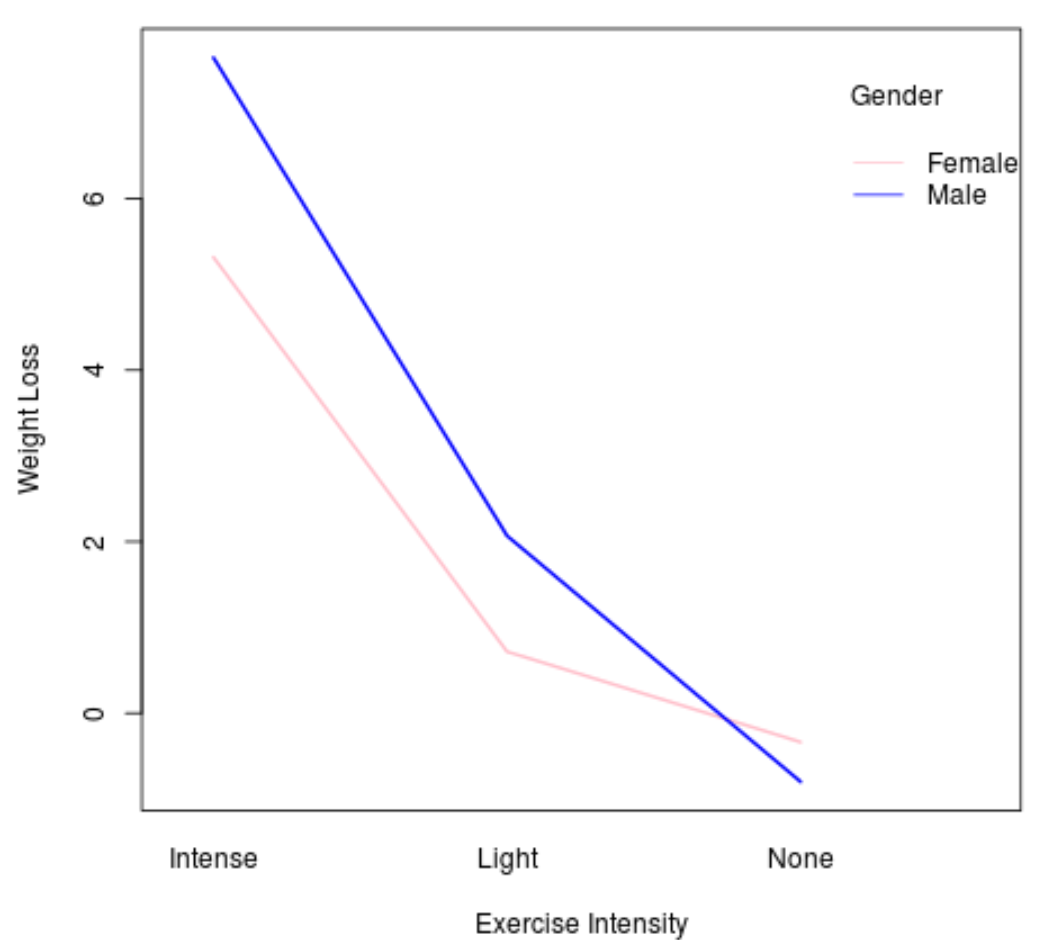
interaction.plot(x.factor = data$exercise, #x-axis variable
trace.factor = data$gender, #variable for lines
response = data$weight_loss, #y-axis variable
fun = median, #metric to plot
ylab = "Weight Loss",
xlab = "Exercise Intensity",
col = c("pink", "blue"),
lty = 1, #line type
lwd = 2, #line width
trace.label = "Gender")

В общем, если две линии на графике взаимодействия параллельны, то эффекта взаимодействия нет. Однако, если линии пересекаются, то, вероятно, существует эффект взаимодействия.
На этом графике мы видим, что линии для мужчин и женщин пересекаются, что указывает на то, что, вероятно, существует эффект взаимодействия между переменными интенсивностью упражнений и полом.
Это соответствует тому факту, что значение p в выходных данных таблицы ANOVA было статистически значимым для члена взаимодействия в модели ANOVA.
Дополнительные ресурсы
Как провести односторонний дисперсионный анализ в R
Как провести двухсторонний ANOVA в R