Однофакторный дисперсионный анализ используется для определения того, приводят ли различные уровни объясняющей переменной к статистически различным результатам в некоторой переменной отклика.
Например, нам может быть интересно понять, приводят ли три уровня образования (степень младшего специалиста, степень бакалавра, степень магистра) к статистически разным годовым доходам. В этом случае у нас есть одна объясняющая переменная и одна переменная отклика.
- Объясняющая переменная: уровень образования
- Переменная ответа: годовой доход
MANOVA — это расширение однофакторного дисперсионного анализа, в котором имеется более одной переменной отклика. Например, нам может быть интересно понять, приводит ли уровень образования к разным годовым доходам и разным суммам долга по студенческим кредитам. В этом случае у нас есть одна объясняющая переменная и две переменные отклика:
- Объясняющая переменная: уровень образования
- Переменные ответа: годовой доход, задолженность по студенческому кредиту.
Поскольку у нас есть более одной переменной отклика, в этом случае было бы уместно использовать MANOVA.
Далее мы объясним, как выполнить MANOVA в Stata.
Пример: MANOVA в Stata
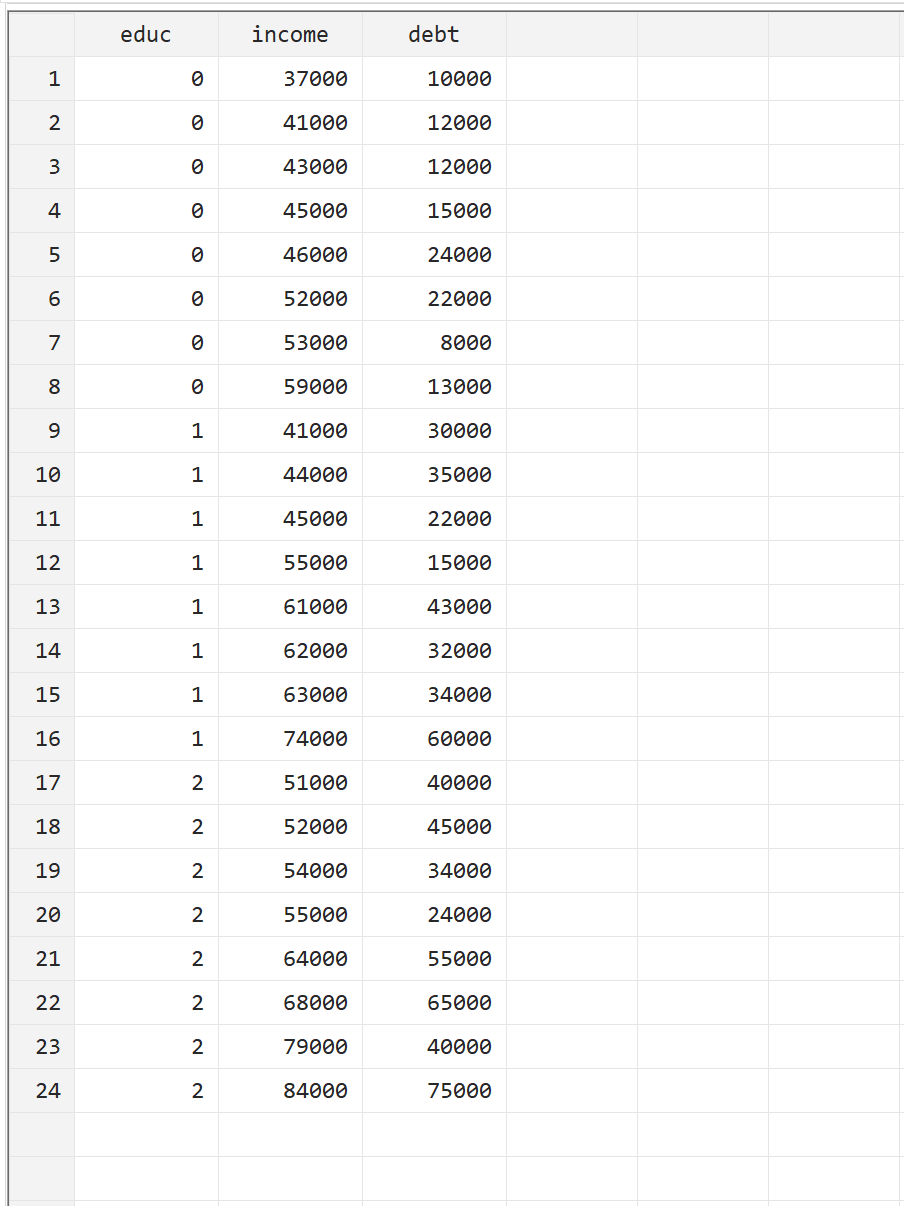
Чтобы проиллюстрировать, как выполнить MANOVA в Stata, мы будем использовать следующий набор данных, который содержит следующие три переменные для 24 человек:
- educ: уровень образования (0 = Associate, 1 = Bachelor, 2 = Master)
- доход: годовой доход
- долг: общая задолженность по студенческому кредиту
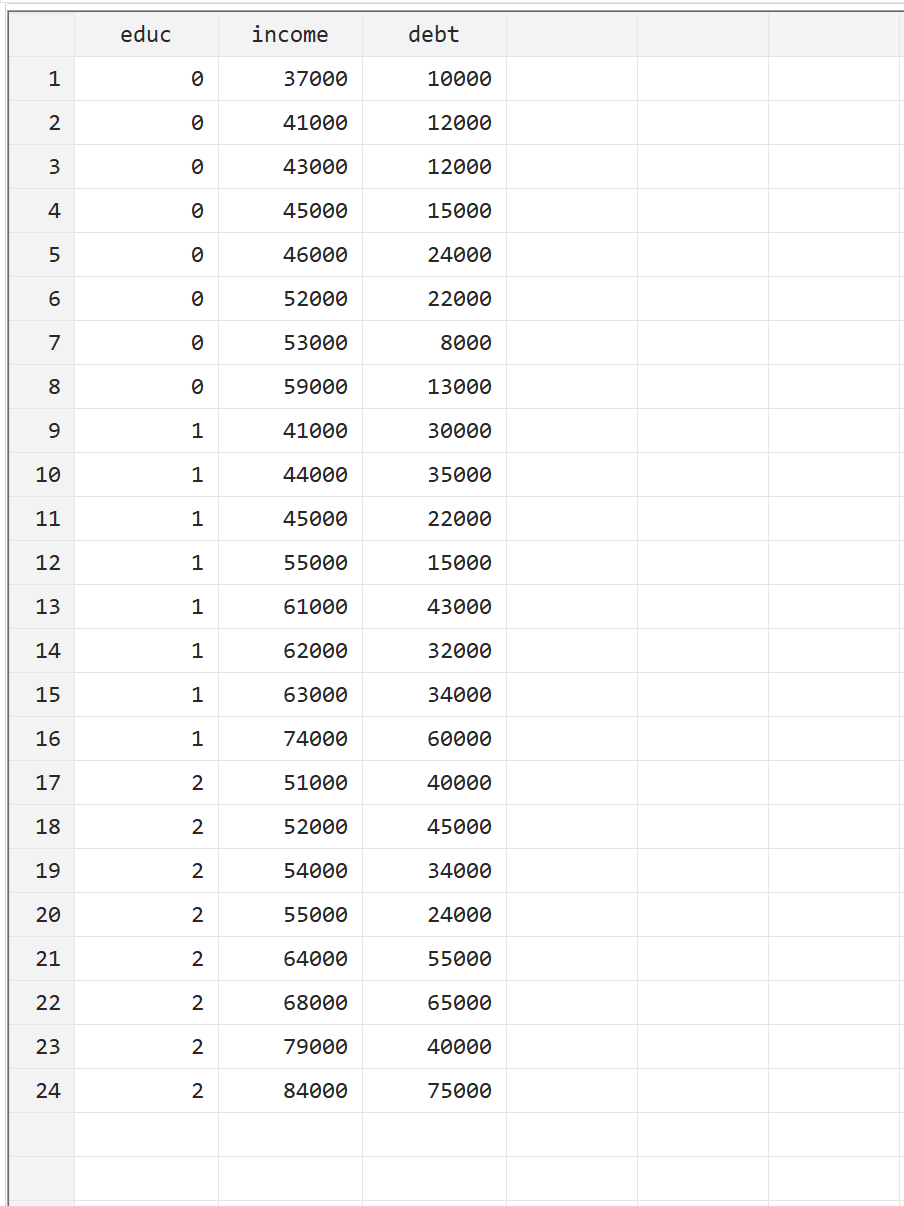
Вы можете воспроизвести этот пример, самостоятельно введя данные вручную, выбрав « Данные» > «Редактор данных» > «Редактор данных» (Правка) в верхней строке меню.
Чтобы выполнить MANOVA, используя образование в качестве объясняющей переменной, а доход и долг в качестве переменных отклика, мы можем использовать следующую команду:
задолженность по доходам manova = образование

Stata выдает четыре уникальных статистических показателя теста вместе с соответствующими значениями p:
Лямбда Уилкса: F-статистика = 5,02, P-значение = 0,0023.
Кривая Пиллаи: F-статистика = 4,07, P-значение = 0,0071.
Кривая Лоули-Хотеллинга: F-статистика = 5,94, P-значение = 0,0008.
Наибольший корень Роя: F-статистика = 13,10, P-значение = 0,0002.
Подробное объяснение того, как рассчитывается статистика каждого теста, см. в этой статье Научного колледжа штата Пенсильвания в Эберли.
Значение p для каждой тестовой статистики меньше 0,05, поэтому нулевая гипотеза будет отклонена независимо от того, какую из них вы используете. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что уровень образования приводит к статистически значимым различиям в годовом доходе и общем студенческом долге.
Примечание о p-значениях: буква рядом со значением p в выходной таблице указывает, как была рассчитана F-статистика (e = точное вычисление, a = приблизительное вычисление, u = верхняя граница).