Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более независимыми переменными и переменной отклика.
В этом руководстве объясняется, как выполнить множественную линейную регрессию в SPSS.
Пример: множественная линейная регрессия в SPSS
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на оценку, которую студент получает на определенном экзамене. Чтобы изучить это, мы можем выполнить множественную линейную регрессию, используя следующие переменные:
Объясняющие переменные:
- Часы обучения
- Сданы подготовительные экзамены
Переменная ответа:
- Оценка экзамена
Используйте следующие шаги, чтобы выполнить эту множественную линейную регрессию в SPSS.
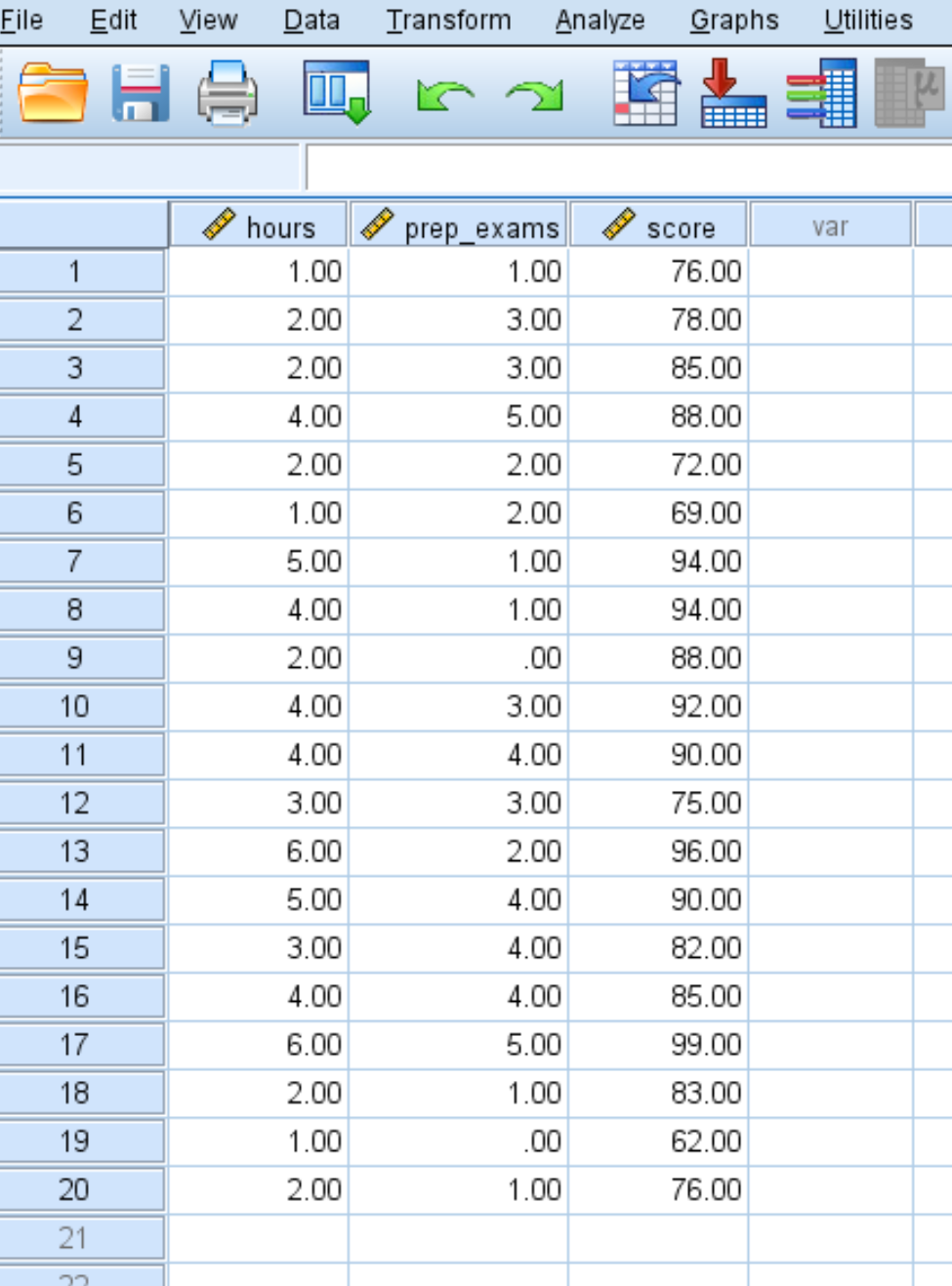
Шаг 1: Введите данные.
Введите следующие данные для количества часов обучения, сданных подготовительных экзаменов и результатов экзаменов, полученных для 20 студентов:
Шаг 2: Выполните множественную линейную регрессию.
Перейдите на вкладку « Анализ », затем « Регрессия », затем « Линейный »:
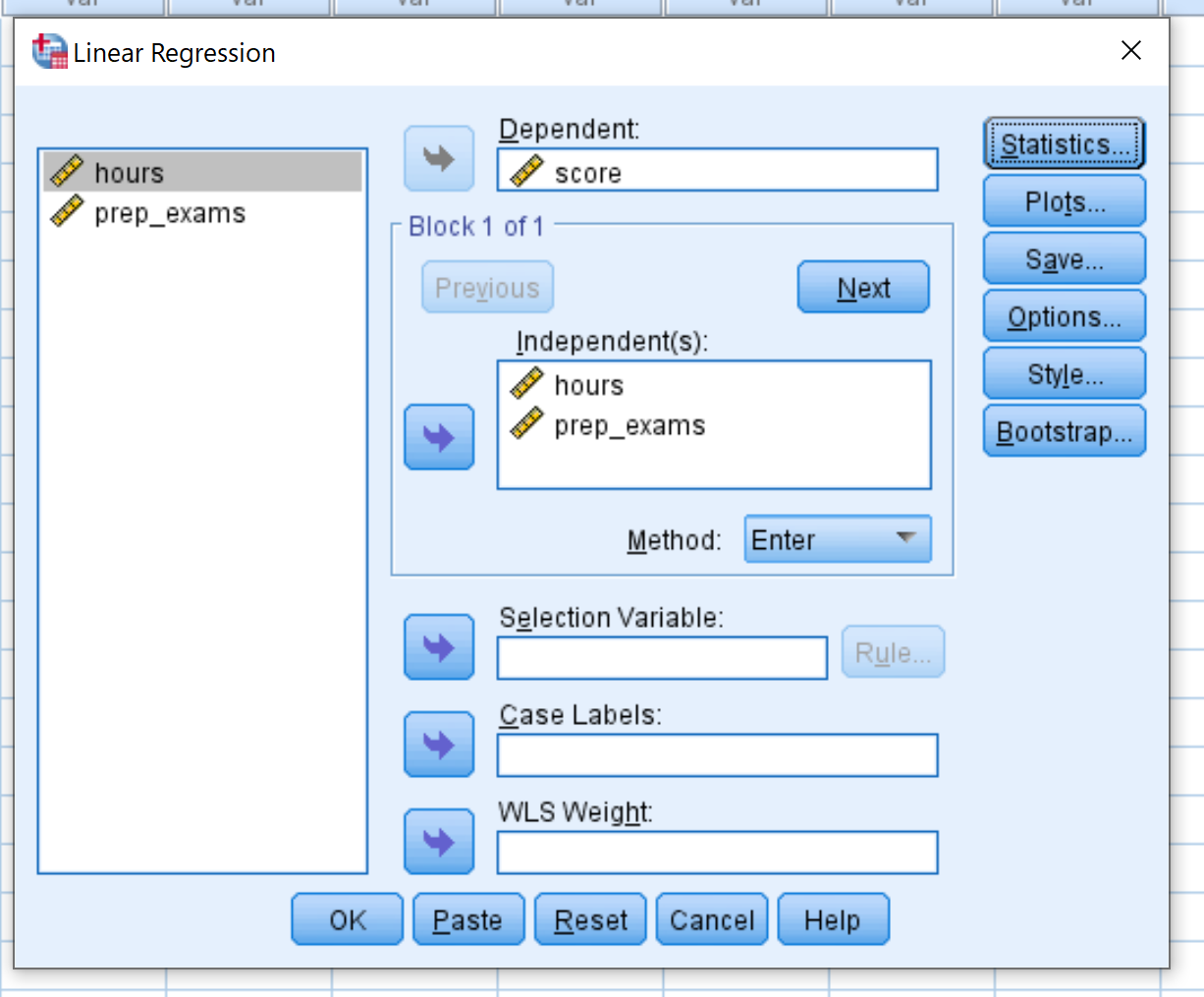
Перетащите переменную оценку в поле с надписью Зависимая. Перетащите переменные hours и prep_exams в поле с надписью Independent(s). Затем нажмите ОК .
Шаг 3: Интерпретируйте вывод.
Как только вы нажмете OK , результаты множественной линейной регрессии появятся в новом окне.
Первая интересующая нас таблица называется « Сводка модели» :
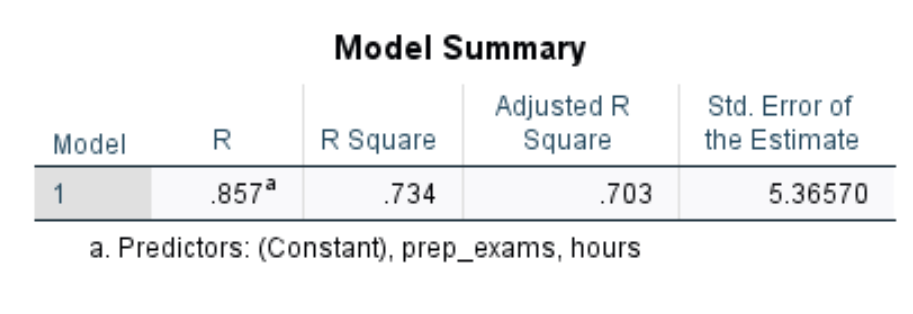
Вот как интерпретировать наиболее важные числа в этой таблице:
- Квадрат R: это доля дисперсии переменной отклика, которая может быть объяснена независимыми переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить часами обучения и количеством сданных подготовительных экзаменов.
- стандарт Ошибка оценки: стандартная ошибка — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,3657 единиц.
Следующая интересующая нас таблица называется ANOVA :
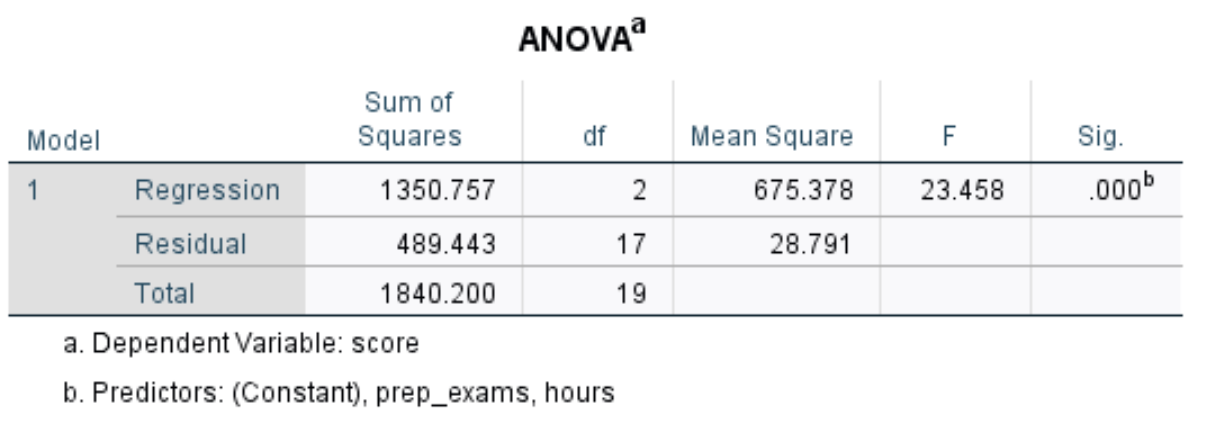
Вот как интерпретировать наиболее важные числа в этой таблице:
- F: это общая статистика F для регрессионной модели, рассчитанная как среднеквадратическая регрессия / среднеквадратичная невязка.
- Sig: это значение p, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение равно 0,000, что указывает на то, что независимые переменные количество часов обучения и сданные подготовительные экзамены имеют статистически значимую связь с экзаменационной оценкой.
Следующая интересующая нас таблица называется « Коэффициенты» :
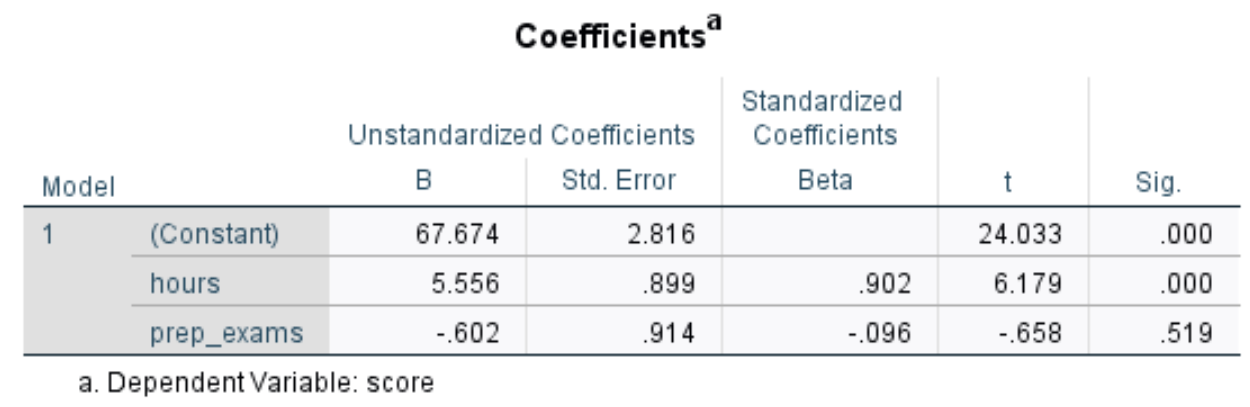
Вот как интерпретировать наиболее важные числа в этой таблице:
- Нестандартизированный B (константа): это говорит нам среднее значение переменной ответа, когда обе переменные-предикторы равны нулю. В этом примере средний балл за экзамен составляет 67,674 , когда количество часов обучения и количество сданных подготовительных экзаменов равны нулю.
- Нестандартизированный B (часы): Это говорит нам о среднем изменении экзаменационного балла, связанном с увеличением количества часов обучения на одну единицу, при условии, что количество сданных подготовительных экзаменов остается постоянным. В этом случае каждый дополнительный час, потраченный на обучение, связан с увеличением экзаменационного балла на 5,556 балла при условии, что количество сданных подготовительных экзаменов остается постоянным.
- Нестандартизированный B (prep_exams): это говорит нам о среднем изменении экзаменационного балла, связанном с увеличением количества сданных подготовительных экзаменов на одну единицу, при условии, что количество часов обучения остается постоянным. В этом случае каждый дополнительный подготовительный экзамен связан со снижением экзаменационного балла на 0,602 балла при условии, что количество часов обучения остается постоянным.
- Сиг. (часы): это p-значение для независимой переменной hours.Поскольку это значение (0,000) меньше 0,05, мы можем сделать вывод, что количество часов обучения статистически значимо связано с экзаменационным баллом.
- Сиг. (prep_exams): это p-значение для пояснительной переменной prep_exams.Поскольку это значение (0,519) не меньше 0,05, мы не можем заключить, что количество сданных подготовительных экзаменов имеет статистически значимую связь с экзаменационной оценкой.
Наконец, мы можем сформировать уравнение регрессии, используя значения, показанные в таблице, для констант , часов и prep_exams.В этом случае уравнение будет таким:
Расчетный балл за экзамен = 67,674 + 5,556*(часы) – 0,602*(подготовительные_экзамены)
Мы можем использовать это уравнение, чтобы найти приблизительную оценку экзамена для учащегося на основе количества часов, которые он проучился, и количества сданных им подготовительных экзаменов. Например, студент, который занимается 3 часа и сдает 2 подготовительных экзамена, должен получить экзаменационный балл 83,1:
Расчетный балл за экзамен = 67,674 + 5,556*(3) – 0,602*(2) = 83,1.
Примечание.* Поскольку независимая переменная «Подготовка к экзаменам » не оказалась статистически значимой, мы можем решить удалить ее из модели и вместо этого выполнить простую линейную регрессию , используя часы обучения* в качестве единственной объясняющей переменной.