Вы можете использовать следующие методы для работы с обычной CDF (кумулятивной функцией распределения) в R:
Метод 1: расчет нормальных вероятностей CDF
#calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)
#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower. tail = FALSE )
Метод 2: постройте нормальный CDF
#define sequence of x-values
x <- seq(-4, 4, .01)
#calculate normal CDF probabilities
prob <- pnorm(x)
#plot normal CDF
plot(x, prob, type=" l ")
Следующие примеры показывают, как использовать эти методы на практике.
Пример 1: Расчет нормальных вероятностей CDF
Следующий код показывает, как вычислить вероятность того, что случайная величина примет значение меньше 1,96 при стандартном нормальном распределении:
#calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)
[1] 0.9750021
Вероятность того, что случайная величина примет значение меньше 1,96 при стандартном нормальном распределении, равна 0,975 .
Мы также можем найти вероятность того, что случайная величина примет значение больше 1,96, используя аргумент lower.tail :
#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower. tail = FALSE )
[1] 0.0249979
И мы можем использовать следующий синтаксис, чтобы найти вероятность того, что случайная величина принимает значение между двумя значениями в стандартном нормальном распределении:
#calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)
[1] 0.9500042
Вероятность того, что случайная величина примет значение от -1,96 до 1,96 при стандартном нормальном распределении, равна 0,95 .
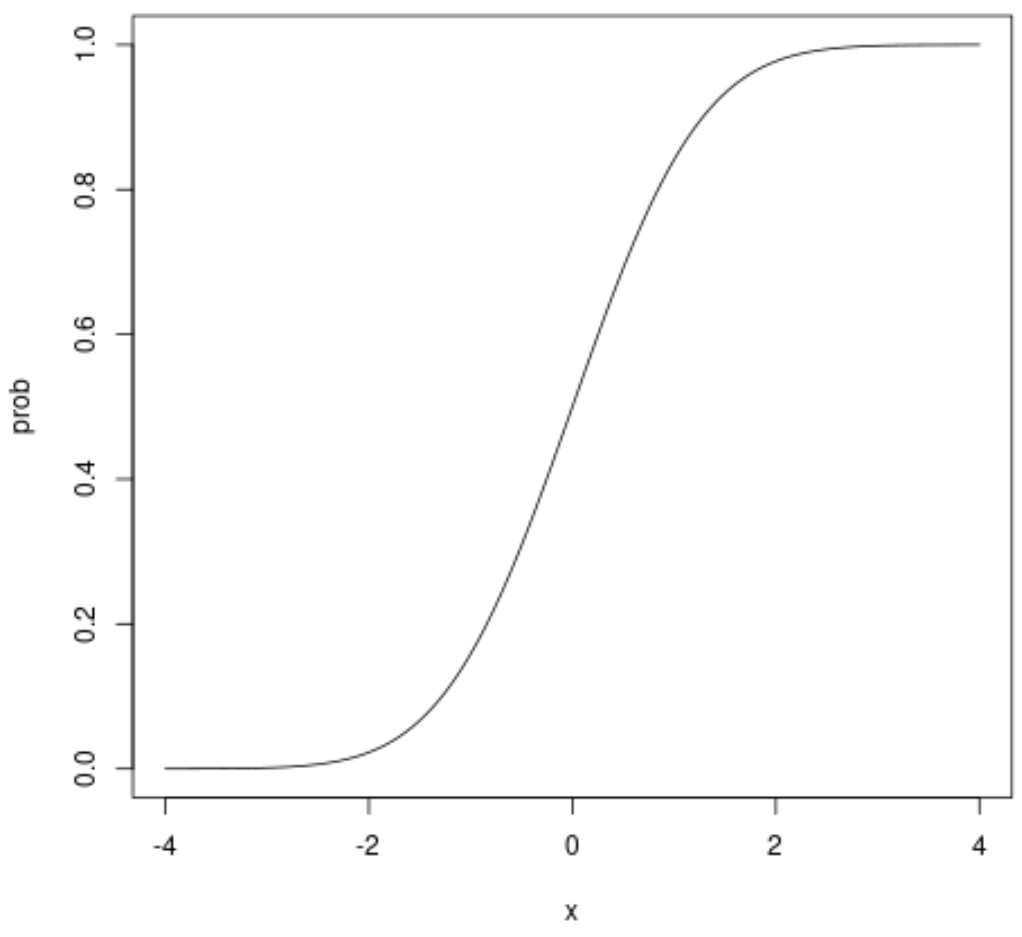
Пример 2: Постройте нормальный CDF
Следующий код показывает, как построить обычный CDF:
#define sequence of x-values
x <- seq(-4, 4, .01)
#calculate normal CDF probabilities
prob <- pnorm(x)
#plot normal CDF
plot(x, prob, type=" l ")
На оси x показаны значения случайной величины, которые соответствуют стандартному нормальному распределению, а на оси y показана вероятность того, что случайная величина примет значение, меньшее, чем значение, показанное на оси x.
Например, если мы посмотрим на x = 1,96, то увидим, что совокупная вероятность того, что x меньше 1,96, составляет примерно 0,975:

Обратите внимание, что вы также можете изменить внешний вид обычного графика CDF:
#define sequence of x-values
x <- seq(-4, 4, .01)
#calculate normal CDF probabilities
prob <- pnorm(x)
#plot normal CDF
plot(x, prob, type='l', col='blue', lwd= 2 , main='Normal CDF', ylab='Cumulative Prob')

Связанный: Как использовать функцию seq в R
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции в R:
Как построить нормальное распределение в R
Как рассчитать Z-значения в R
Руководство по dnorm, pnorm, qnorm и rnorm в R