Однофакторный дисперсионный анализ («дисперсионный анализ») сравнивает средние значения трех или более независимых групп, чтобы определить, существует ли статистически значимая разница между соответствующими средними значениями генеральной совокупности.
В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ вручную.
Пример. Однофакторный дисперсионный анализ вручную
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзаменам к разным средним баллам на определенном экзамене. Чтобы проверить это, мы набираем 30 студентов для участия в исследовании и разделяем их на три группы.
Студенты в каждой группе случайным образом назначаются для использования одной из трех программ подготовки к экзамену в течение следующих трех недель для подготовки к экзамену. По истечении трех недель все студенты сдают один и тот же экзамен.
Ниже представлены результаты экзаменов для каждой группы:
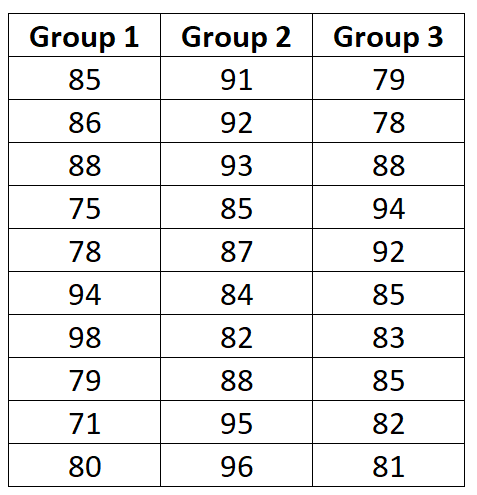
Используйте следующие шаги, чтобы вручную выполнить однофакторный дисперсионный анализ, чтобы определить, различается ли средний балл за экзамен между тремя группами:
Шаг 1: Рассчитайте среднее для группы и общее среднее.
Во-первых, мы рассчитаем среднее значение для всех трех групп вместе с общим средним значением:
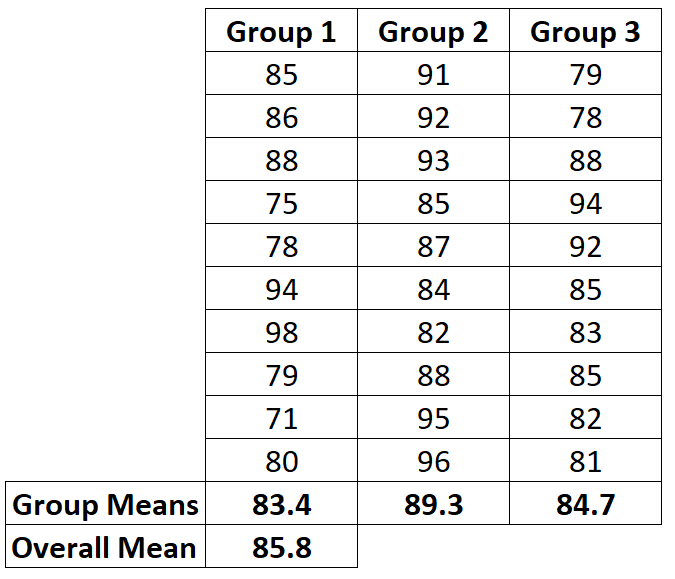
Шаг 2: Рассчитайте SSR.
Далее мы рассчитаем сумму квадратов регрессии (SSR) по следующей формуле:
nΣ(X j – X ..) 2
куда:
- n : размер выборки группы j
- Σ : греческий символ, означающий «сумма».
- X j : среднее значение группы j
- X .. : общее среднее значение
В нашем примере мы вычисляем, что SSR = 10(83,4-85,8) 2 + 10(89,3-85,8) 2 + 10(84,7-85,8) 2 = 192,2
Шаг 3: Рассчитайте SSE.
Далее мы рассчитаем сумму квадратов ошибок (SSE) по следующей формуле:
Σ( Xij – Xj ) 2
куда:
- Σ : греческий символ, означающий «сумма».
- X ij : i -е наблюдение в группе j
- X j : среднее значение группы j
В нашем примере мы вычисляем SSE следующим образом:
1 группа: (85-83,4) 2 + (86-83,4) 2 +(88-83,4) 2 +(75-83,4) 2 +(78-83,4) 2 +(94-83,4) 2 +(98-83,4) 2 +(79-83,4) 2 +(71-83,4) 2 +(80-83,4) 2 = 640,4
2 группа: (91-89,3) 2 + (92-89,3) 2 +(93-89,3) 2 +(85-89,3) 2 +(87-89,3) 2 +(84-89,3) 2 +(82-89,3) 2 +(88-89,3) 2 +(95-89,3) 2 +(96-89,3) 2 = 208,1
3 группа: (79-84,7) 2 + (78-84,7) 2 +(88-84,7) 2 +(94-84,7) 2 +(92-84,7) 2 +(85-84,7) 2 +(83-84,7) 2 +(85-84,7) 2 +(82-84,7) 2 +(81-84,7) 2 = 252,1
ССЭ: 640,4 + 208,1 + 252,1 = 1100,6
Шаг 4: Рассчитайте SST.
Далее мы рассчитаем общую сумму квадратов (SST) по следующей формуле:
SST = SSR + SSE
В нашем примере SST = 192,2 + 1100,6 = 1292,8.
Шаг 5: Заполните таблицу ANOVA.
Теперь, когда у нас есть SSR, SSE и SST, мы можем заполнить таблицу ANOVA:
| Источник | Сумма квадратов (СС) | дф | Средние квадраты (MS) | Ф | | --- | --- | --- | --- | --- | | Уход | 192,2 | 2 | 96,1 | 2,358 | | Ошибка | 1100,6 | 27 | 40,8 | | | Общий | 1292,8 | 29 | | |
Вот как мы рассчитали различные числа в таблице:
- обработка df: k-1 = 3-1 = 2
- ошибка df: nk = 30-3 = 27
- df всего: n-1 = 30-1 = 29
- Лечение MS: лечение SST / df = 192,2 / 2 = 96,1
- Ошибка MS: ошибка SSE/df = 1100,6/27 = 40,8
- F: обработка МС/ошибка МС = 96,1/40,8 = 2,358.
Примечание: n = общее количество наблюдений, k = количество групп.
Шаг 6: Интерпретируйте результаты.
Статистика F-теста для этого однофакторного дисперсионного анализа составляет 2,358.Чтобы определить, является ли это статистически значимым результатом, мы должны сравнить его с критическим значением F, найденным в таблице распределения F со следующими значениями:
- α (уровень значимости) = 0,05
- DF1 (числитель степеней свободы) = df обработки = 2
- DF2 (степени свободы в знаменателе) = ошибка df = 27
Мы находим, что критическое значение F равно 3,3541 .
Поскольку статистика F-теста в таблице ANOVA меньше критического значения F в таблице F-распределения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы сказать, что существует статистически значимая разница между средними экзаменационными баллами трех групп.
Дополнительный ресурс: используйте этот калькулятор однофакторного дисперсионного анализа для автоматического выполнения однофакторного дисперсионного анализа до пяти образцов.