Коэффициент корреляции Пирсона (также известный как «коэффициент корреляции продукта и момента») является мерой линейной связи между двумя переменными X и Y. Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Формула для нахождения коэффициента корреляции Пирсона
Формула для нахождения коэффициента корреляции Пирсона, обозначаемого как r , для выборки данных ( из Википедии ):

Скорее всего, вам никогда не придется вычислять эту формулу вручную, так как вы можете использовать программное обеспечение, чтобы сделать это за вас, но полезно иметь представление о том, что именно делает эта формула, на примере.
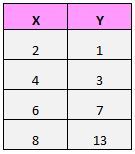
Предположим, у нас есть следующий набор данных:
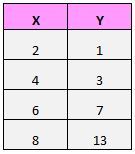
Если мы нанесем эти пары (X, Y) на диаграмму рассеяния, это будет выглядеть так:
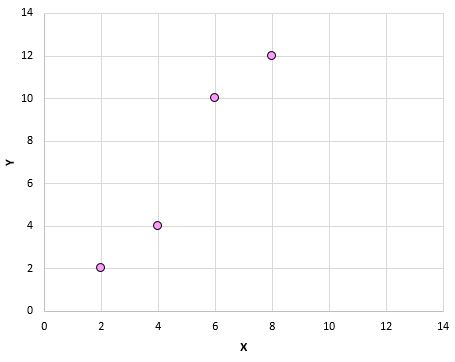
Просто взглянув на эту диаграмму рассеяния, мы можем сказать, что существует положительная связь между переменными X и Y: когда X увеличивается, Y также имеет тенденцию к увеличению. Но чтобы точно определить, насколько положительно связаны эти две переменные, нам нужно найти коэффициент корреляции Пирсона.
Давайте сосредоточимся только на числителе формулы:

Для каждой пары (X, Y) в нашем наборе данных нам нужно найти разницу между значением x и средним значением x, разницей между значением y и средним значением y, а затем умножить эти два числа вместе.
Например, наша первая пара (X, Y) — это (2, 2). Среднее значение x в этом наборе данных равно 5, а среднее значение y в этом наборе данных равно 7. Таким образом, разница между значением x в этой паре и средним значением x составляет 2 – 5 = -3. Разница между значением y в этой паре и средним значением y составляет 2 – 7 = -5. Затем, когда мы перемножаем эти два числа вместе, мы получаем -3 * -5 = 15.
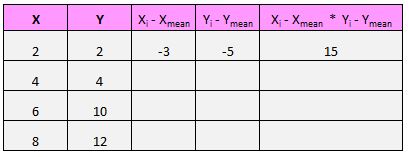
Вот визуальный взгляд на то, что мы только что сделали:
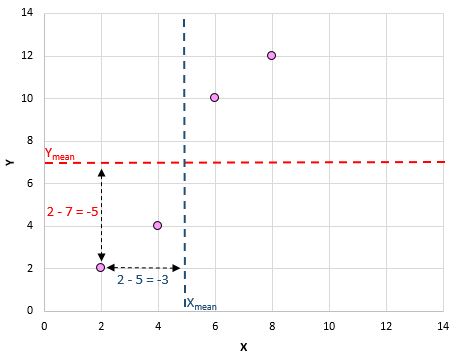
Далее нам просто нужно сделать это для каждой отдельной пары:
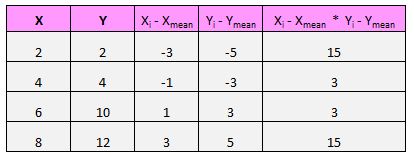
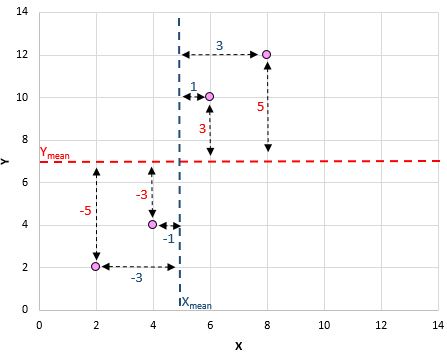
Последний шаг для получения числителя формулы — просто сложить все эти значения:
15 + 3 + 3 + 15 = 36
Затем знаменатель формулы говорит нам найти сумму всех квадратов разностей для x и y, затем умножить эти два числа вместе, а затем извлечь квадратный корень:

Итак, сначала мы найдем сумму квадратов разностей для x и y:
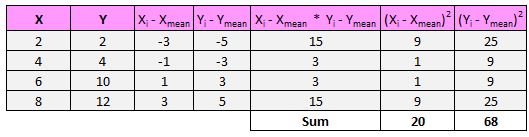
Затем мы перемножим эти два числа вместе: 20 * 68 = 1360.
Наконец, мы возьмем квадратный корень: √ 1360 = 36,88 .
Итак, мы нашли, что числитель формулы равен 36, а знаменатель равен 36,88. Это означает, что наш коэффициент корреляции Пирсона равен r = 36/36,88 = 0,976.
Это число близко к 1, что указывает на сильную положительную линейную связь между нашими переменными X и Y. Это подтверждает взаимосвязь, которую мы видели на диаграмме рассеяния.
Визуализация корреляций
Напомним, что коэффициент корреляции Пирсона говорит нам о типе линейной связи (положительная, отрицательная, отсутствие) между двумя переменными, а также о силе этой связи (слабая, умеренная, сильная).
Когда мы строим диаграмму рассеяния двух переменных, мы можем видеть реальную связь между двумя переменными. Вот множество различных типов линейных отношений, которые мы можем увидеть:
Сильная, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки расположены плотно друг к другу, что указывает на прочную связь.
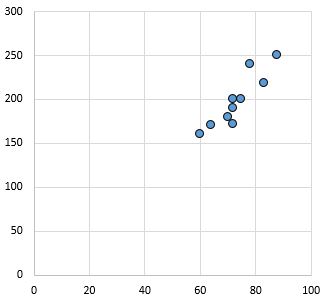
Коэффициент корреляции Пирсона: 0,94
Слабая, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки довольно разбросаны, что указывает на слабую связь.
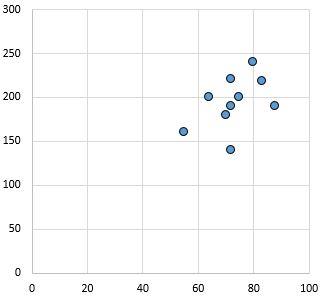
Коэффициент корреляции Пирсона: 0,44
Нет взаимосвязи: нет четкой взаимосвязи (положительной или отрицательной) между переменными.
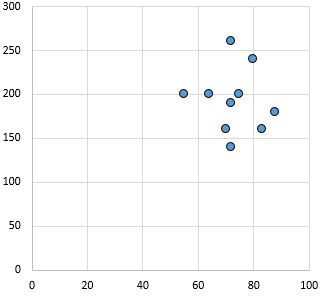
Коэффициент корреляции Пирсона: 0,03
Сильная, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки расположены плотно друг к другу, что указывает на сильную связь.
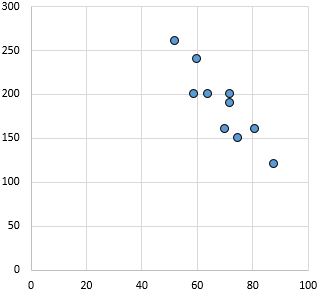
Коэффициент корреляции Пирсона: -0,87
Слабая, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки довольно разбросаны, что указывает на слабую связь.
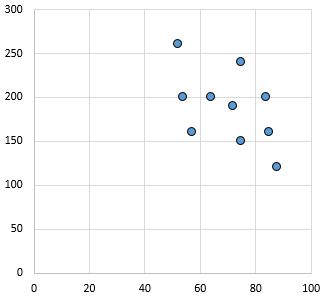
Коэффициент корреляции Пирсона: – 0,46
Проверка значимости коэффициента корреляции Пирсона
Когда мы находим коэффициент корреляции Пирсона для набора данных, мы часто работаем с выборкой данных, полученной из большей совокупности.Это означает, что можно найти ненулевую корреляцию для двух переменных, даже если они фактически не коррелированы в генеральной совокупности.
Например, предположим, что мы делаем диаграмму рассеяния для переменных X и Y для каждой точки данных во всей совокупности, и она выглядит следующим образом:
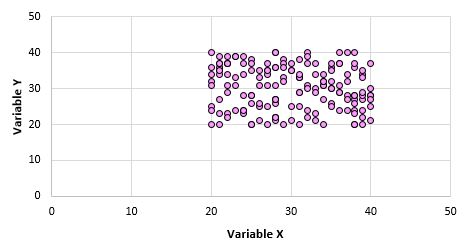
Ясно, что эти две переменные не коррелированы. Однако возможно, что когда мы берем выборку из 10 точек из генеральной совокупности, мы выбираем следующие точки:
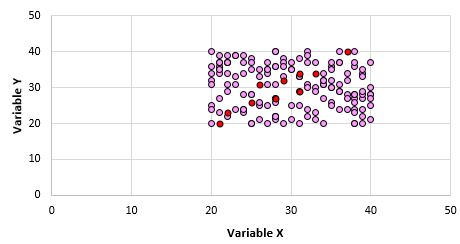
Мы можем обнаружить, что коэффициент корреляции Пирсона для этой выборки точек равен 0,93, что указывает на сильную положительную корреляцию, несмотря на то, что корреляция населения равна нулю.
Чтобы проверить, является ли корреляция между двумя переменными статистически значимой, мы можем найти следующую тестовую статистику:
Тестовая статистика T = r * √ (n-2) / (1-r 2 )
где n — количество пар в нашей выборке, r — коэффициент корреляции Пирсона, а тестовая статистика T следует за распределением с n-2 степенями свободы.
Давайте рассмотрим пример того, как проверить значимость коэффициента корреляции Пирсона.
Пример
Следующий набор данных показывает рост и вес 12 человек:
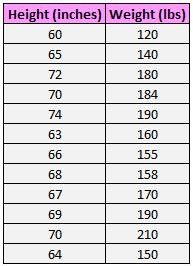
Диаграмма рассеяния ниже показывает значение этих двух переменных:
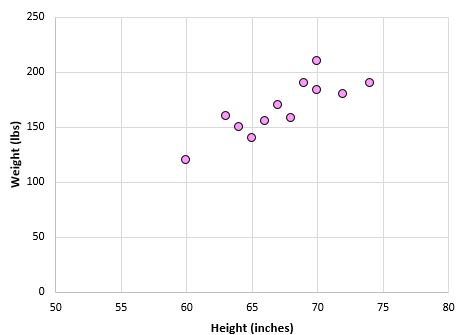
Коэффициент корреляции Пирсона для этих двух переменных составляет r = 0,836.
Статистика теста T = 0,836 * √ (12 -2) / (1-0,836 2 ) = 4,804.
Согласно нашему калькулятору распределения t , при оценке 4,804 с 10 степенями свободы p-значение равно 0,0007. Поскольку 0,0007 < 0,05, мы можем заключить, что корреляция между весом и ростом в этом примере является статистически значимой при альфа = 0,05.
Предостережения
Хотя коэффициент корреляции Пирсона может быть полезен для определения того, имеют ли две переменные линейную связь, мы должны помнить о трех вещах при интерпретации коэффициента корреляции Пирсона:
1. Корреляция не подразумевает причинно-следственной связи. Тот факт, что две переменные коррелированы, не означает, что одна из них обязательно вызывает более или менее частое появление другой. Классическим примером этого является положительная корреляция между продажами мороженого и нападениями акул. Когда продажи мороженого увеличиваются в определенное время года, количество нападений акул также увеличивается.
Означает ли это, что потребление мороженого вызывает нападения акул? Конечно нет! Это просто означает, что летом как потребление мороженого, так и нападения акул, как правило, увеличиваются, поскольку летом мороженое более популярно, а летом больше людей ходят в океан.
2. Корреляции чувствительны к выбросам. Один экстремальный выброс может резко изменить коэффициент корреляции Пирсона. Рассмотрим пример ниже:
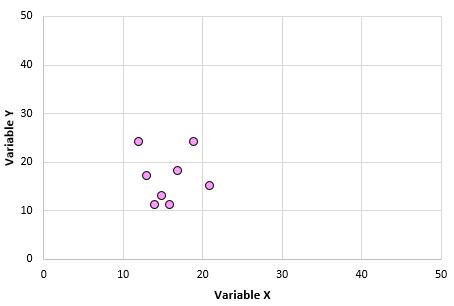
Переменные X и Y имеют коэффициент корреляции Пирсона 0,00.Но представьте, что у нас есть один выброс в наборе данных:
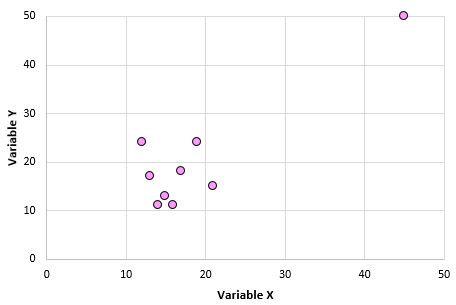
Теперь коэффициент корреляции Пирсона для этих двух переменных равен 0,878.Один этот выброс меняет все. Вот почему, когда вы вычисляете корреляцию для двух переменных, рекомендуется визуализировать переменные с помощью диаграммы рассеяния для проверки выбросов.
3. Коэффициент корреляции Пирсона не фиксирует нелинейные отношения между двумя переменными. Представьте, что у нас есть две переменные со следующими отношениями:
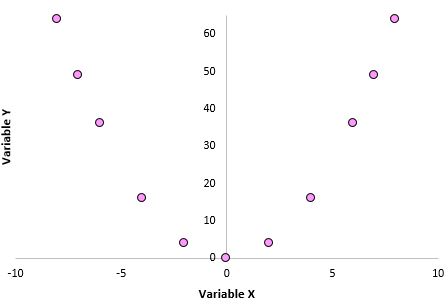
Коэффициент корреляции Пирсона для этих двух переменных равен 0,00, поскольку между ними нет линейной зависимости. Однако эти две переменные имеют нелинейную связь: значения y — это просто квадрат значений x.
При использовании коэффициента корреляции Пирсона помните, что вы просто проверяете, связаны ли две переменные линейно.Даже если коэффициент корреляции Пирсона говорит нам, что две переменные не коррелированы, они все равно могут иметь некоторую нелинейную связь. Это еще одна причина, по которой полезно создавать диаграмму рассеяния при анализе взаимосвязи между двумя переменными — это может помочь вам обнаружить нелинейную взаимосвязь.