В статистике простая линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим простую линейную регрессию, мы получаем «линию наилучшего соответствия», которая описывает взаимосвязь между x и y, которую можно записать как:
ŷ = б 0 + б 1 х
куда:
- ŷ - прогнозируемое значение переменной отклика
- b 0 - точка пересечения с осью y
- b 1 – коэффициент регрессии
- x - значение переменной-предиктора
Иногда мы заинтересованы в использовании этой линии наилучшего соответствия для построения интервала предсказания для заданного значения x 0 , который является интервалом вокруг предсказанного значения ŷ 0 таким образом, что существует 95% вероятность того, что реальное значение y в население, соответствующее x 0 , находится внутри этого интервала.
Формула для расчета интервала прогнозирования для заданного значения x 0 записывается как:
ŷ 0 +/- t α/2,df=n-2 * se
куда:
se = S yx √(1 + 1/n + (x 0 – x ) 2 /SS x )
Формула может показаться немного пугающей, но на самом деле ее легко вычислить в Excel. Далее мы рассмотрим пример использования этой формулы для расчета интервала прогнозирования для заданного значения в Excel.
Пример: как построить интервал прогнозирования в Excel
Следующий набор данных показывает количество часов обучения вместе с экзаменационными баллами, полученными 15 разными студентами:
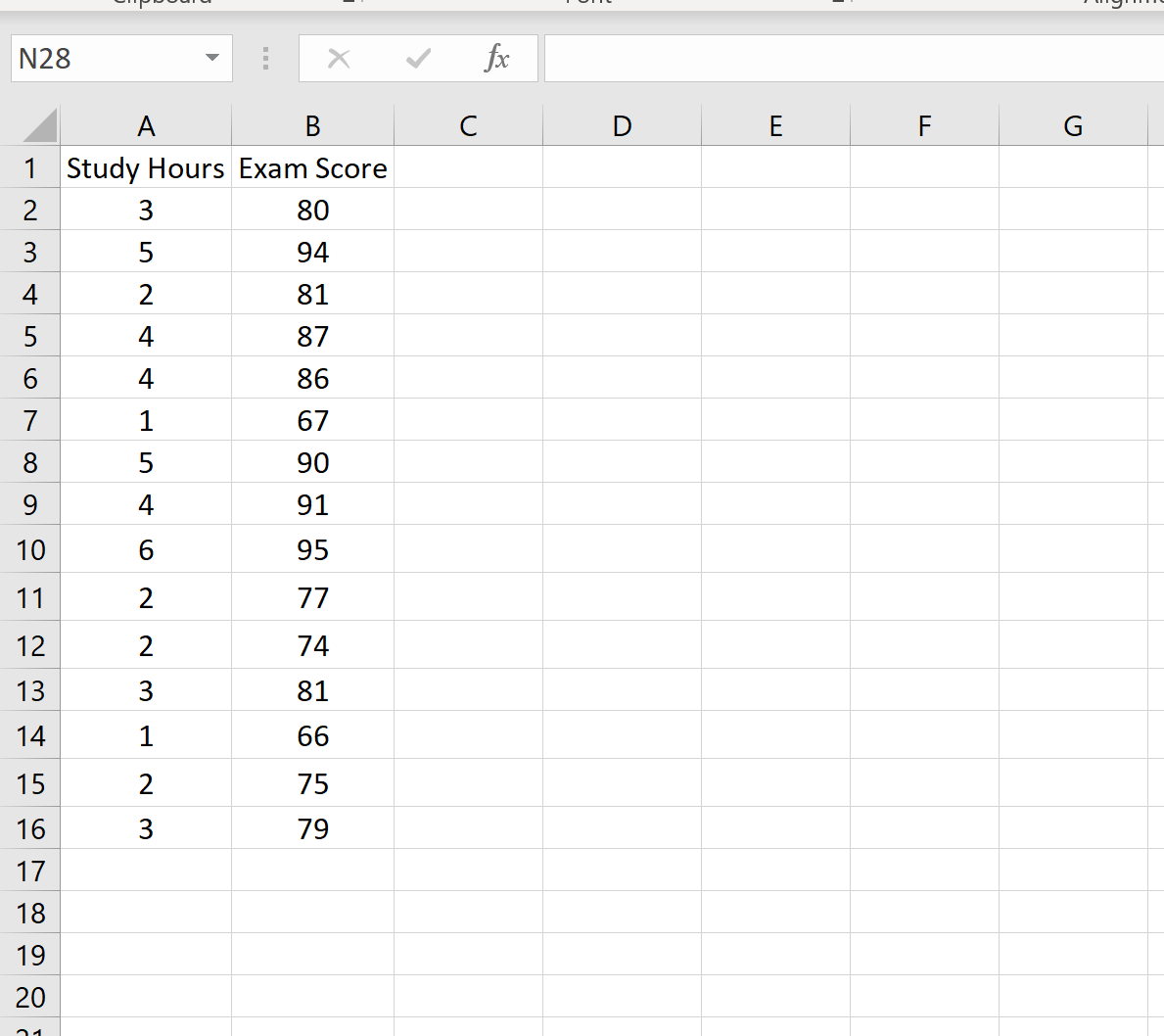
Предположим, мы хотим создать 95-процентный интервал предсказания для значения x 0 = 3. То есть мы хотим создать такой интервал, при котором существует 95-процентная вероятность того, что результат экзамена находится в пределах этого интервала для студента, который учится на 3 часа.
На следующем снимке экрана показано, как рассчитать все необходимые значения для получения этого интервала прогнозирования.
Примечание.Формулы в столбце F показывают, как были рассчитаны значения в столбце E.
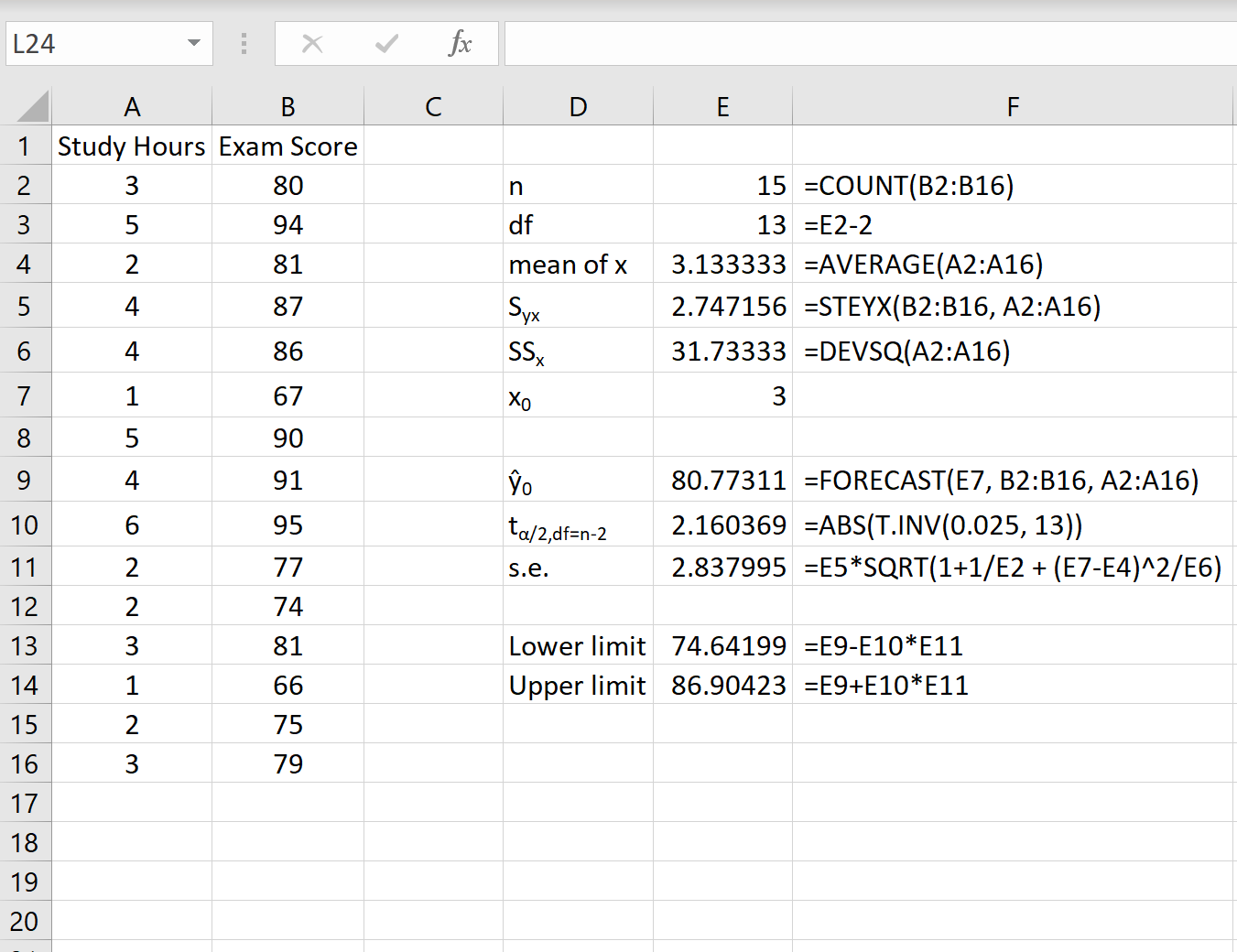
Интервал предсказания 95% для значения x 0 = 3 равен (74,64, 86,90).То есть мы прогнозируем с вероятностью 95%, что студент, который занимается 3 часа, получит от 74,64 до 86,90 баллов.
Несколько замечаний по используемым расчетам:
- Чтобы вычислить t-критическое значение t α/2,df=n-2 , мы использовали α/2 = 0,05/2 = 0,25, поскольку нам нужен интервал прогнозирования 95%. Обратите внимание, что более высокие интервалы прогнозирования (например, интервал прогнозирования 99%) приведут к более широким интервалам. И наоборот, более низкий интервал прогнозирования (например, интервал прогнозирования 90%) приведет к более узкому интервалу.
- Мы использовали формулу =ПРОГНОЗ() , чтобы получить предсказанное значение для ŷ 0 , но формула =ПРОГНОЗ.ЛИНЕЙНАЯ() вернет точно такое же значение.