В статистике студенты часто путают два термина: вероятность и пропорция .
Вот разница:
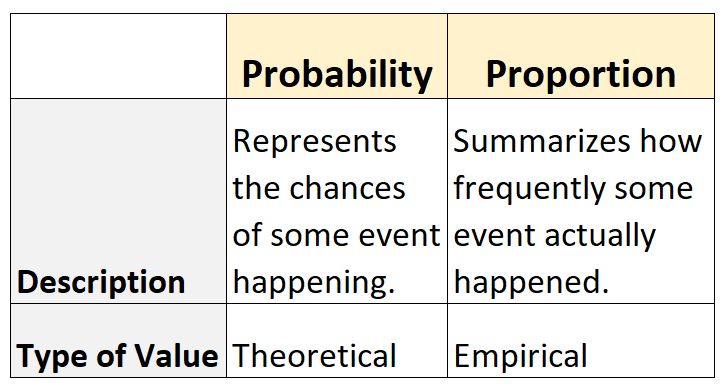
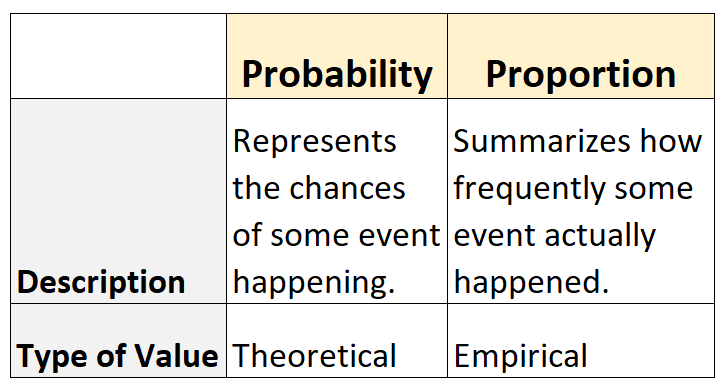
- Вероятность представляет шансы того, что какое-то событие произойдет. Это теоретически .
- Пропорция обобщает, как часто какое-то событие действительно происходило. Это эмпирический .
Мы часто используем вероятность, когда говорим о вероятности того, что какое-то событие произойдет в будущем.
Напротив, мы часто используем пропорцию, когда описываем, как часто какое-либо событие действительно происходило в прошлом.
Следующие примеры иллюстрируют различия между вероятностями и пропорциями в разных сценариях.
Пример 1: Вероятность и пропорция при подбрасывании монеты
Если мы подбросим правильную монету, вероятность того, что она упадет орлом, составит 0,5 или 50% .
Однако если мы подбросим правильную монету 20 раз, то сможем подсчитать, сколько раз она выпадала орлом. Например, возможно, он приземлился орлом в 60% подбрасываний.
Вероятность выпадения орла является теоретической, но процентное соотношение случаев, когда монета выпадало орлом, является эмпирическим — мы могли бы подсчитать эту пропорцию.
Пример 2: Вероятность и пропорция в бросках кубиков
Если мы бросим шестигранный кубик, вероятность того, что на нем выпадет число «4», составляет 1/6 или около 16,67% .
Однако, если мы бросим кубик 10 раз, то сможем подсчитать долю случаев, когда он выпал на 4. Например, возможно, он выпал на 4 в 20% бросков.
Вероятность выпадения «4» является теоретической, но доля случаев, когда кубик выпадал на «4», является эмпирической — мы могли бы подсчитать пропорцию.
Пример 3: Вероятность и пропорция в спиннерах
Если мы вращаем спиннер, разделенный на четыре равные части — красную, синюю, зеленую и фиолетовую, — вероятность того, что он приземлится на фиолетовый цвет при любом заданном вращении, составляет 25% .
Однако, если мы повернем спиннер 100 раз, то сможем подсчитать, сколько раз он приземлялся на фиолетовый цвет. Например, возможно, он приземлился на фиолетовый во время 15% вращений.
Вероятность того, что спиннер приземлится на фиолетовый цвет, является теоретической, но доля случаев, когда он приземлялся на фиолетовый цвет, является эмпирической — мы могли бы посчитать эту пропорцию.
Пример 4: Вероятность против доли в колодах карт
В стандартной колоде из 52 карт 4 дамы. Таким образом, вероятность выбора королевы при любом случайном розыгрыше составляет 4/52 = 7,69% .
Однако, если мы возьмем случайное взятие (и заменим вытянутую карту) 50 раз, мы сможем подсчитать долю случаев, когда мы вытягиваем даму. Например, возможно, мы рисуем даму в 10% розыгрышей.
Вероятность выбора ферзя является теоретической, но доля случаев, когда мы на самом деле выбираем королеву, является эмпирической — мы могли бы посчитать пропорцию.
Дополнительные ресурсы
Вероятность и вероятность: в чем разница?
Закон полной вероятности: определение и примеры