График QQ , сокращенно от «квантильный-квантильный» график, часто используется для оценки того, потенциально ли набор данных получен из некоторого теоретического распределения.
В большинстве случаев этот тип графика используется для определения того, соответствует ли набор данных нормальному распределению .
В этом руководстве объясняется, как создать график QQ для набора данных в Python.
Пример: график QQ в Python
Предположим, у нас есть следующий набор данных из 100 значений:
import numpy as np
#create dataset with 100 values that follow a normal distribution
np.random.seed(0)
data = np.random.normal(0,1, 1000)
#view first 10 values
data[:10]
array([ 1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799,
-0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985 ])
Чтобы создать график QQ для этого набора данных, мы можем использовать функцию qqplot() из библиотеки statsmodels:
import statsmodels.api as sm
import matplotlib.pyplot as plt
#create Q-Q plot with 45-degree line added to plot
fig = sm.qqplot(data, line='45')
plt.show()
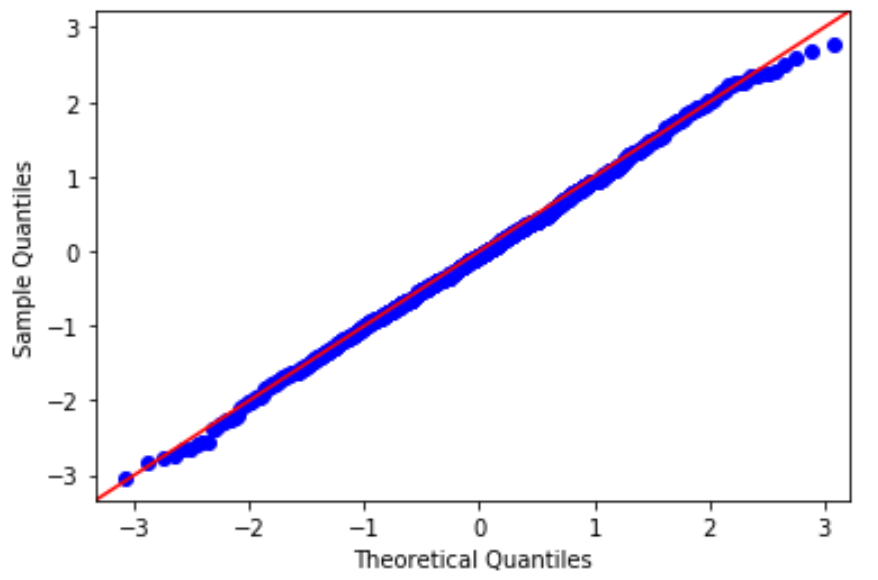
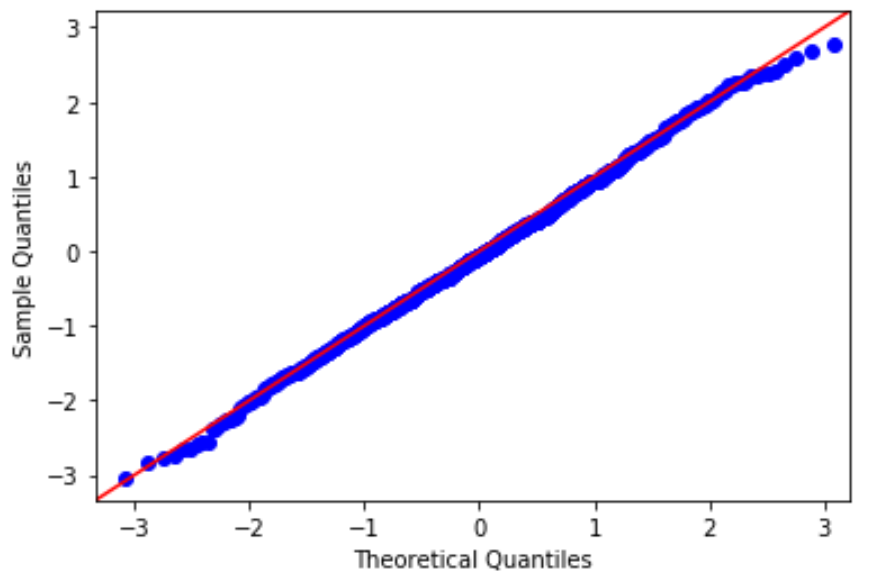
На графике QQ ось X отображает теоретические квантили.Это означает, что он не показывает ваши фактические данные, а вместо этого показывает, где ваши данные были бы, если бы они были нормально распределены.
Ось Y отображает ваши фактические данные.Это означает, что если значения данных падают примерно по прямой линии под углом 45 градусов, то данные распределяются нормально.
Мы можем видеть на нашем графике QQ выше, что значения данных имеют тенденцию близко следовать 45-градусному, что означает, что данные, вероятно, нормально распределены. Это не должно удивлять, поскольку мы сгенерировали 100 значений данных с помощью функции numpy.random.normal() .
Вместо этого рассмотрим, если бы мы создали набор данных из 100 равномерно распределенных значений и создали график QQ для этого набора данных:
#create dataset of 100 uniformally distributed values
data = np.random.uniform(0,1, 1000)
#generate Q-Q plot for the dataset
fig = sm.qqplot(data, line='45')
plt.show()
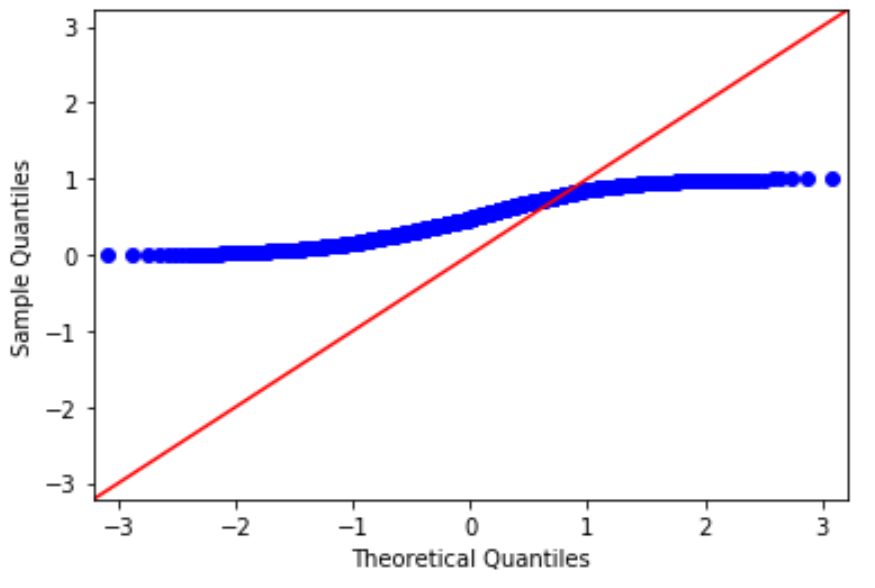
Значения данных явно не соответствуют красной линии под углом 45 градусов, что указывает на то, что они не следуют нормальному распределению.
Примечания к графикам QQ
Имейте в виду следующие примечания о графиках QQ:
- Хотя график QQ не является формальным статистическим тестом, он предлагает простой способ визуально проверить, нормально ли распределен набор данных.
- Будьте осторожны, чтобы не спутать графики QQ с графиками PP , которые используются реже и не так полезны для анализа значений данных, попадающих на крайние хвосты распределения.
Вы можете найти больше руководств по Python здесь .