Когда две переменные имеют линейную связь, вы часто можете использовать простую линейную регрессию для количественной оценки их связи.
Однако простая линейная регрессия не работает, когда две переменные имеют нелинейную связь. В этих случаях можно попробовать использовать квадратичную регрессию .
В этом руководстве объясняется, как выполнить квадратичную регрессию в SPSS.
Пример: квадратичная регрессия в SPSS
Предположим, нам интересно понять взаимосвязь между количеством отработанных часов и счастьем. У нас есть следующие данные о количестве отработанных часов в неделю и сообщаемом уровне счастья (по шкале от 0 до 100) для 16 разных людей:
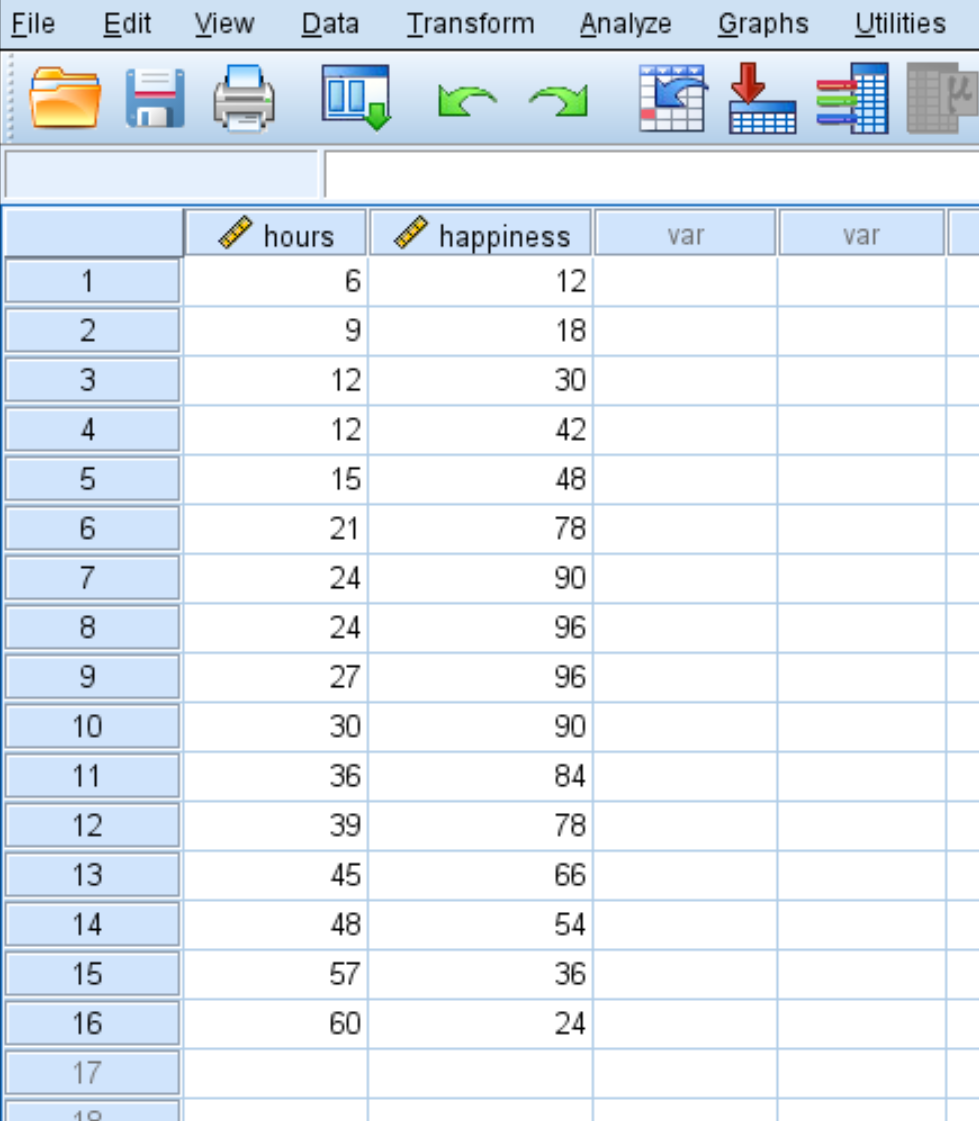
Используйте следующие шаги, чтобы выполнить квадратичную регрессию в SPSS.
Шаг 1: Визуализируйте данные.
Прежде чем выполнять квадратичную регрессию, давайте построим диаграмму рассеяния, чтобы визуализировать взаимосвязь между отработанными часами и счастьем, чтобы убедиться, что две переменные действительно имеют квадратичную взаимосвязь.
Перейдите на вкладку « Графики », затем « Построитель диаграмм »:
В появившемся новом окне выберите Scatter/Dot в списке Choose from.Затем перетащите диаграмму с названием Simple Scatter в главное окно редактирования. Перетащите переменные часы на ось X, а счастье — на ось Y. Затем нажмите ОК .
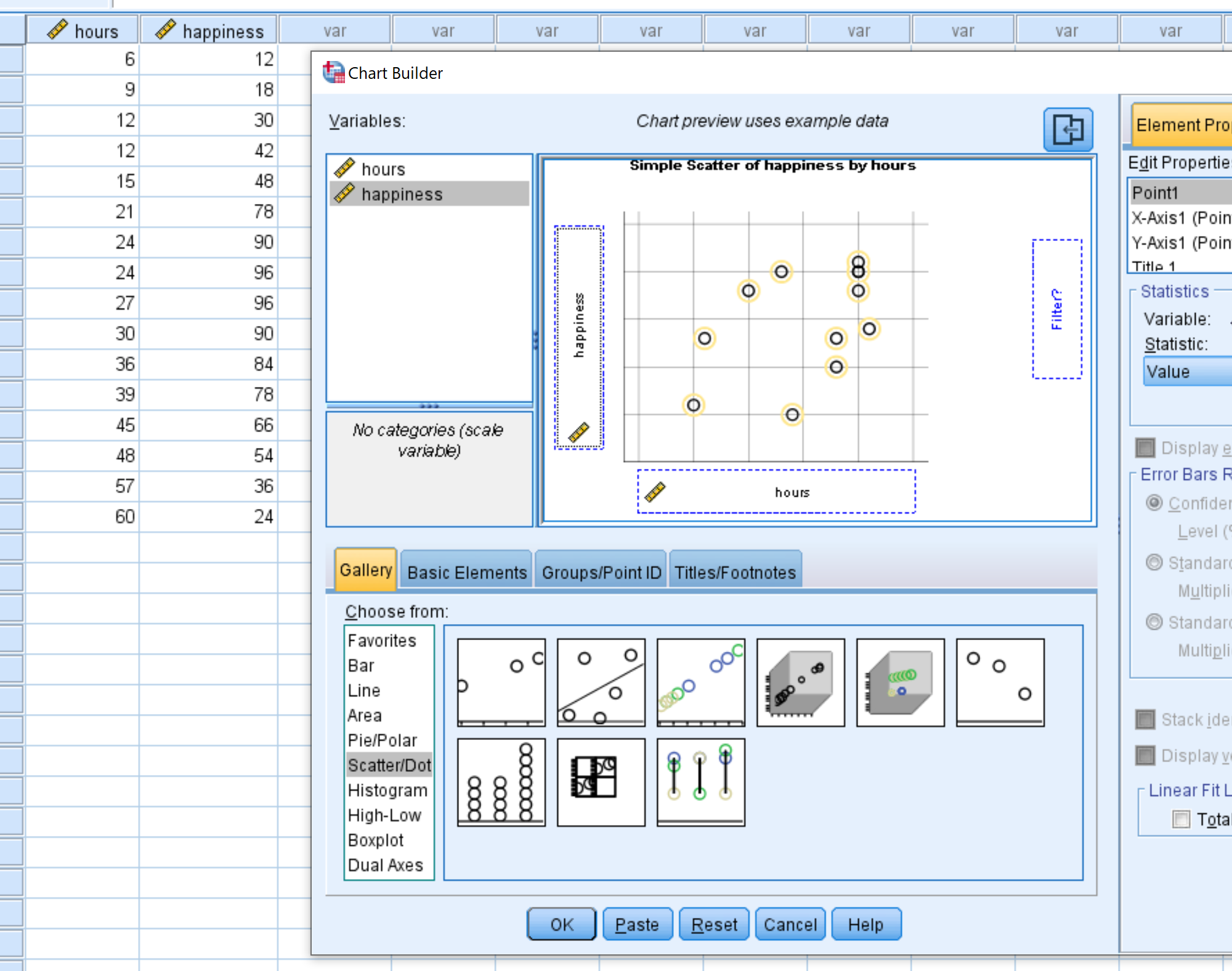
Появится следующая диаграмма рассеяния:
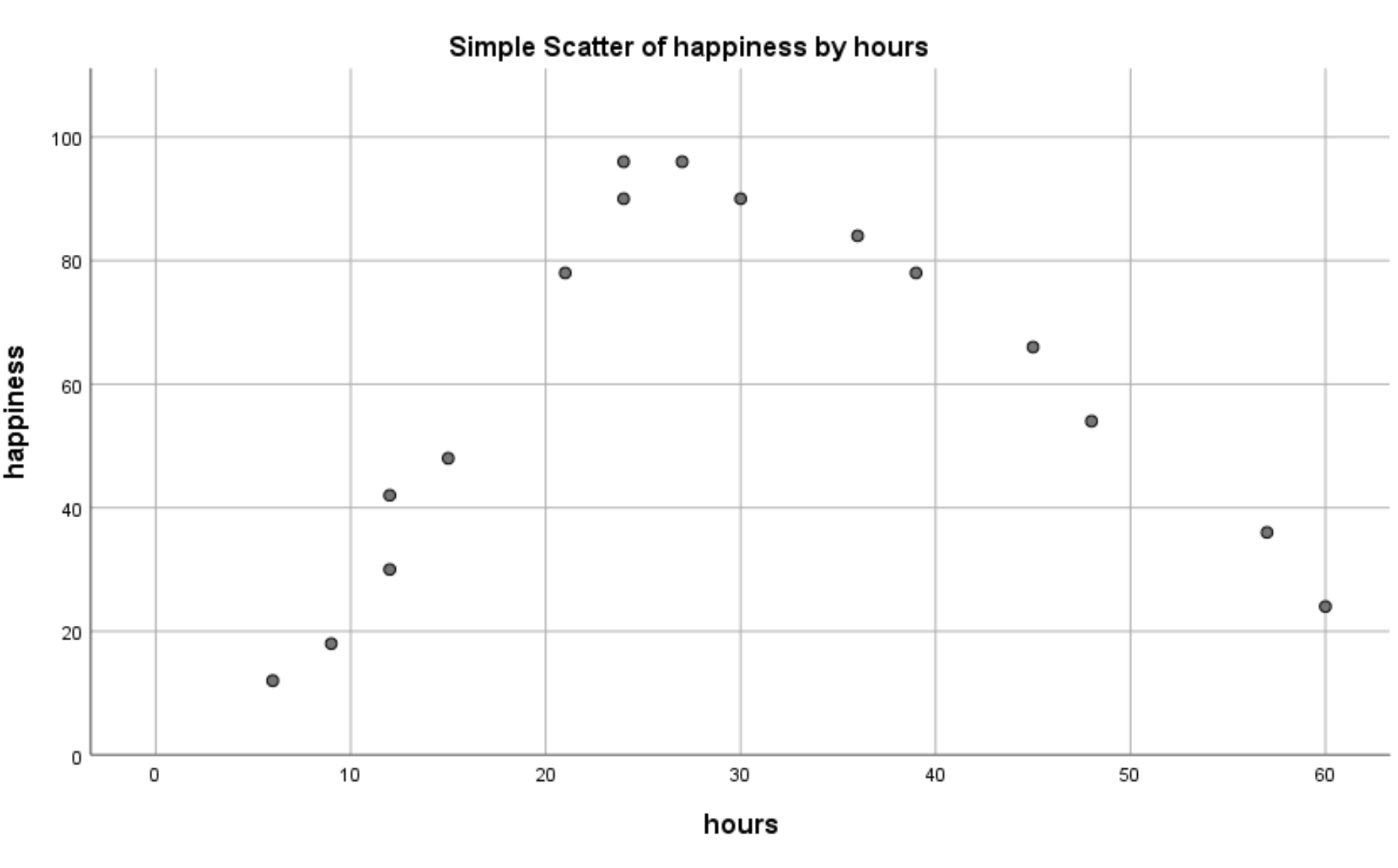
Мы можем ясно видеть, что существует нелинейная зависимость между количеством отработанных часов и счастьем. Это говорит нам о том, что квадратичная регрессия является подходящим методом для использования в этой ситуации.
Шаг 2: Создайте новую переменную.
Прежде чем мы сможем выполнить квадратичную регрессию, нам нужно создать предикторную переменную для часов 2 .
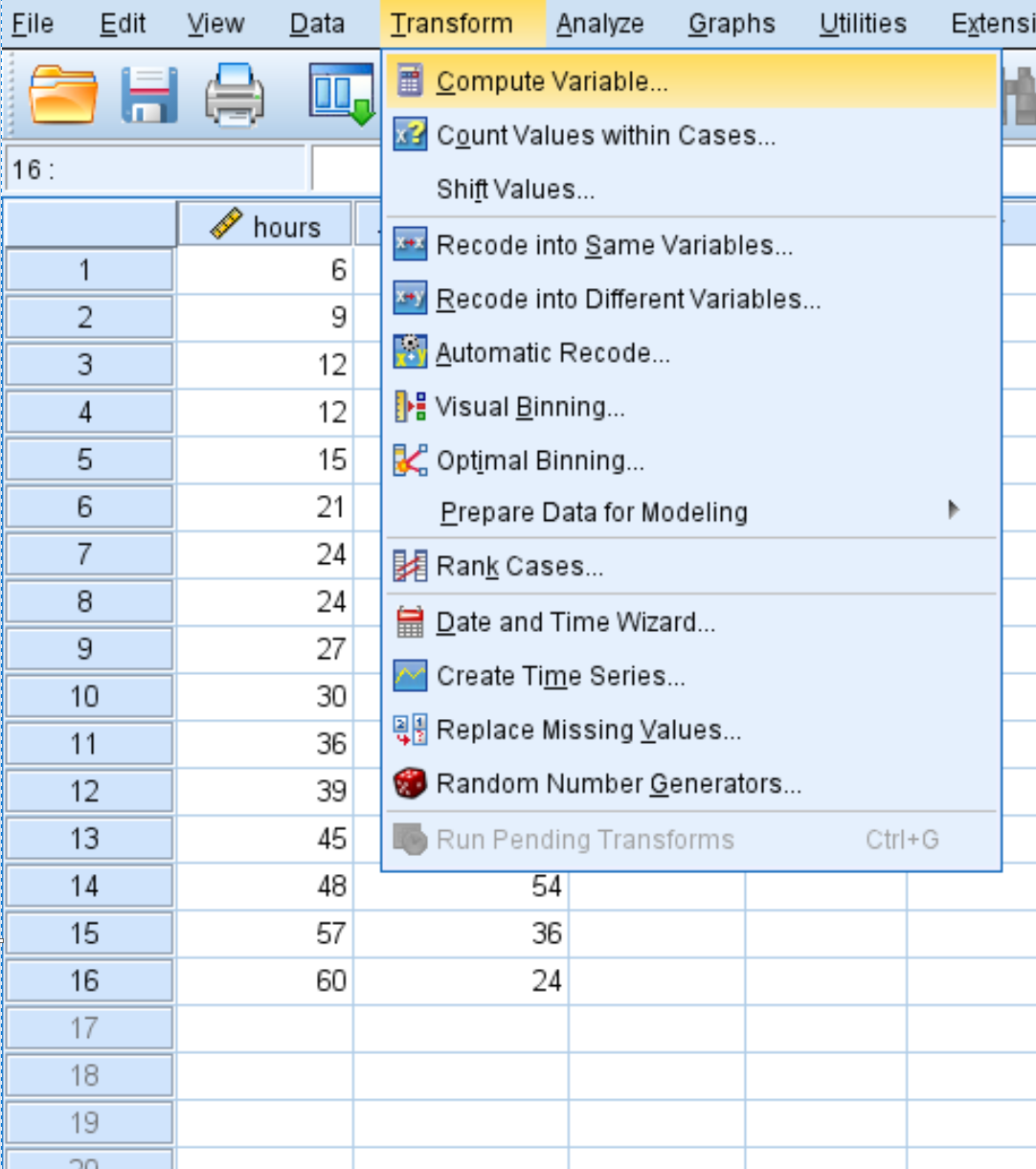
Перейдите на вкладку « Преобразование », затем « Вычислить переменную »:
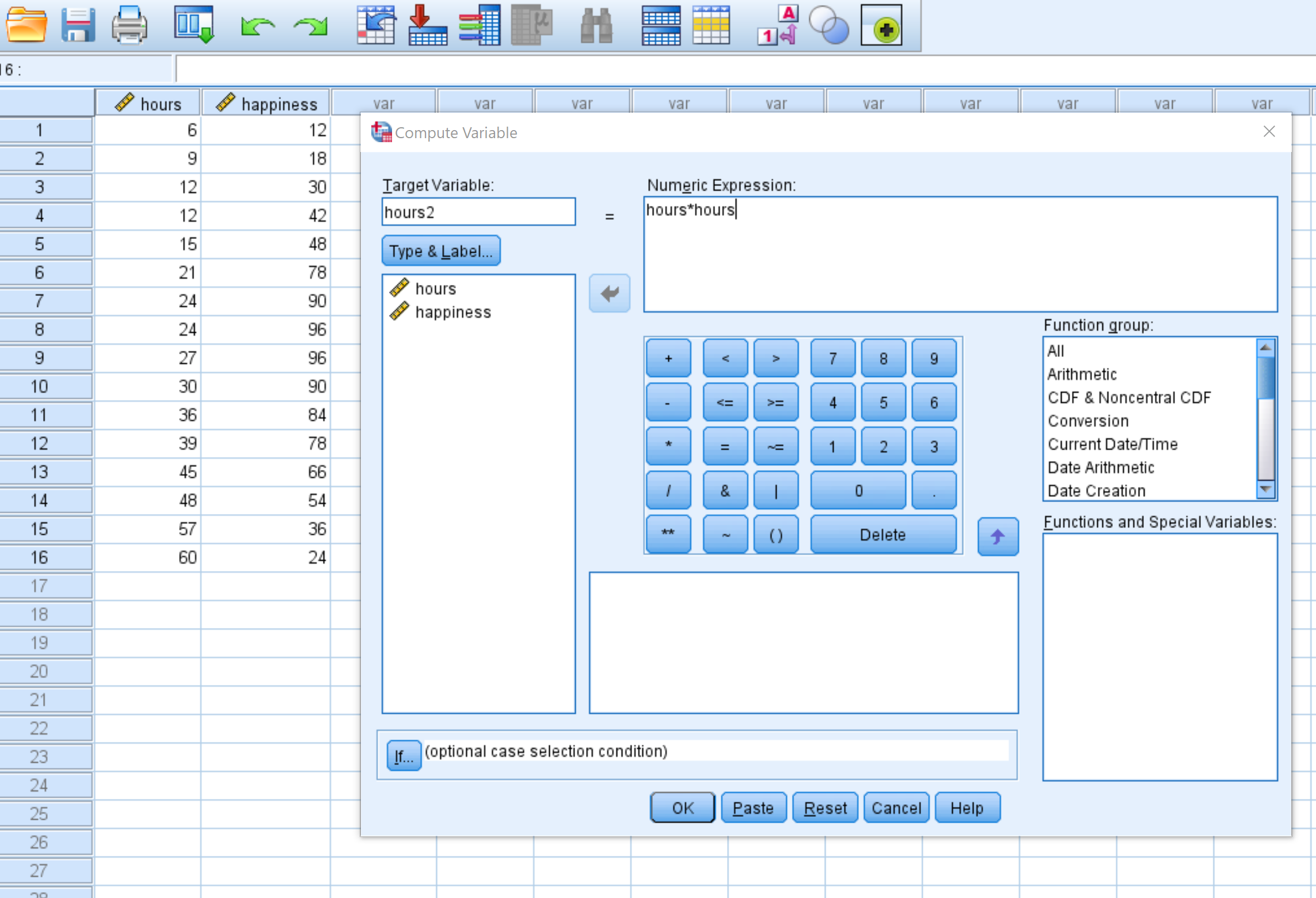
В новом появившемся окне назовите целевую переменную hours2 и определите ее как hours*hours :
Как только вы нажмете OK , переменная hours2 появится в новом столбце:
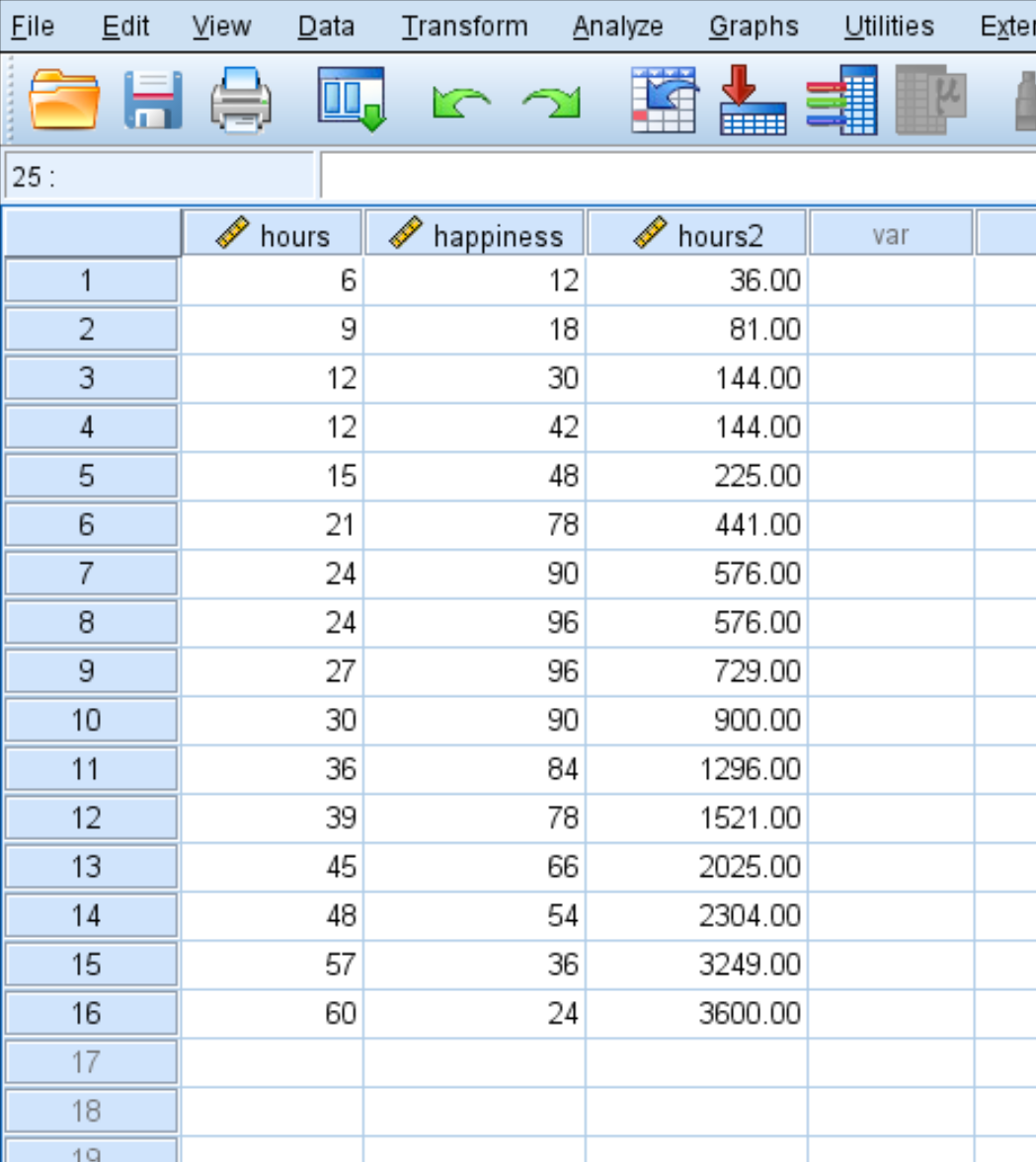
Шаг 3: Выполните квадратичную регрессию.
Далее мы выполним квадратичную регрессию. Перейдите на вкладку « Анализ », затем « Регрессия », затем « Линейный »:
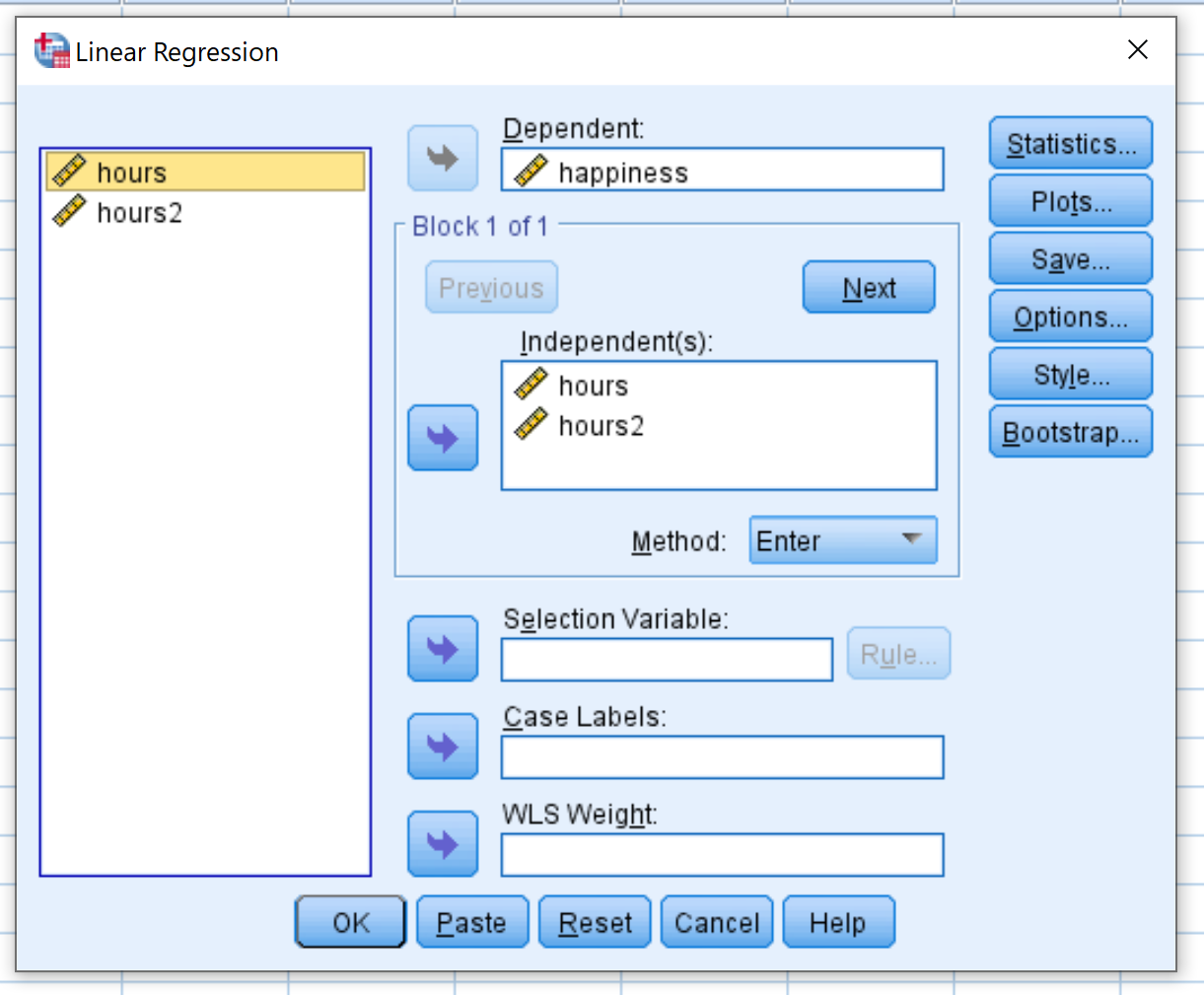
В появившемся новом окне перетащите счастье в поле с надписью Зависимое. Перетащите часы и часы2 в поле с надписью «Независимые». Затем нажмите ОК .
Шаг 4: Интерпретируйте результаты.
Как только вы нажмете OK , результаты квадратичной регрессии появятся в новом окне.
Первая интересующая нас таблица называется « Сводка модели» :

Вот как интерпретировать наиболее важные числа в этой таблице:
- Квадрат R: это доля дисперсии переменной отклика, которая может быть объяснена независимыми переменными. В этом примере 90,9% вариаций счастья можно объяснить переменными часами и часами 2 .
- стандарт Ошибка оценки: стандартная ошибка — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 9,519 единиц.
Следующая интересующая нас таблица называется ANOVA :
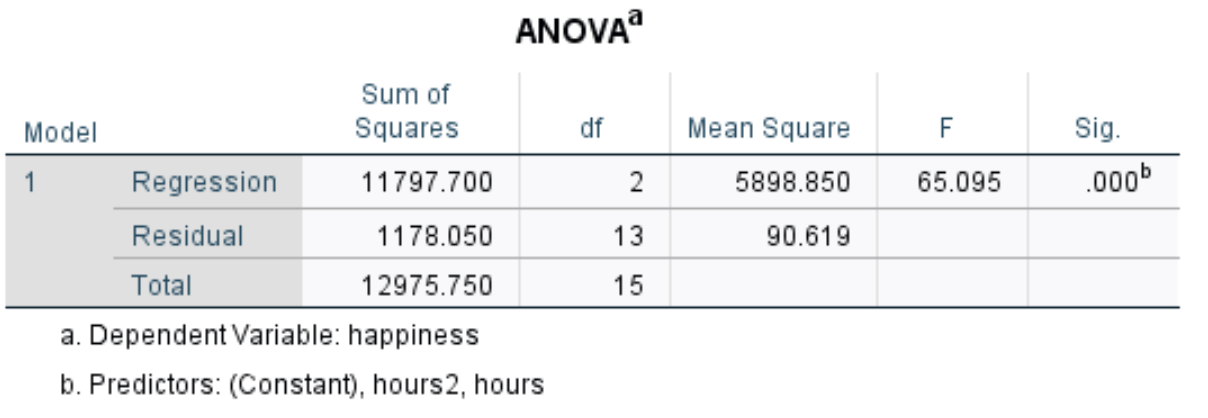
Вот как интерпретировать наиболее важные числа в этой таблице:
- F: это общая статистика F для регрессионной модели, рассчитанная как среднеквадратическая регрессия / среднеквадратичная невязка.
- Sig: это значение p, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. В этом случае p-значение равно 0,000, что указывает на то, что независимые переменные часы и часы 2 вместе взятые имеют статистически значимую связь с экзаменационной оценкой.
Следующая интересующая нас таблица называется « Коэффициенты» :
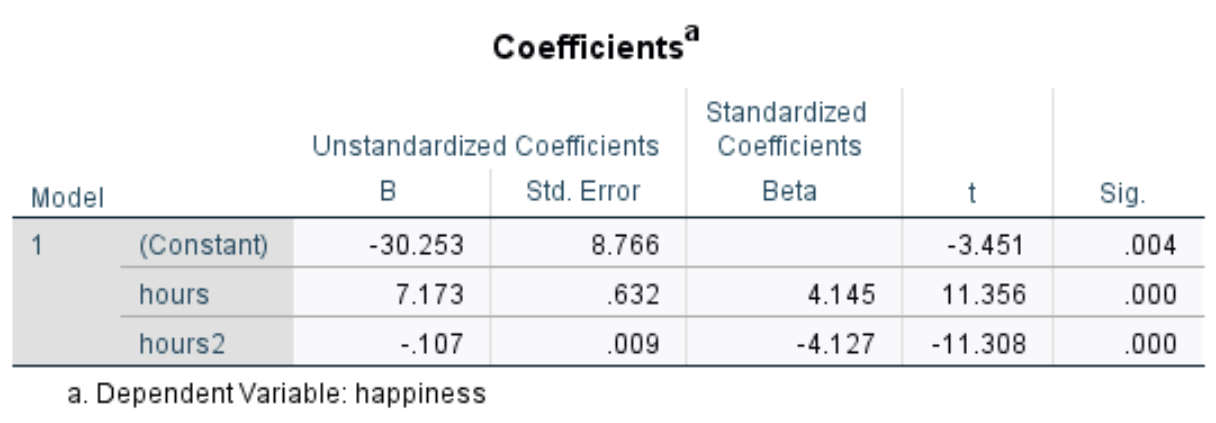
Мы можем использовать значения в столбце Unstandardized B , чтобы сформировать оценочное уравнение регрессии для этого набора данных:
Предполагаемый уровень счастья = -30,253 + 7,173*(часы) – 0,107*(часы 2 )
Мы можем использовать это уравнение, чтобы найти предполагаемый уровень счастья для человека на основе количества часов, которые он работает в неделю. Например, ожидается, что человек, который работает 60 часов в неделю, будет иметь уровень счастья 14,97:
Предполагаемый уровень счастья = -30,253 + 7,173*(60) – 0,107*(60 2 ) = 14,97 .
И наоборот, человек, который работает 30 часов в неделю, по прогнозам, будет иметь уровень счастья 88,65:
Предполагаемый уровень счастья = -30,253 + 7,173*(30) – 0,107*(30 2 ) = 88,65 .
Шаг 5: Сообщите о результатах.
Наконец, мы хотим сообщить о результатах нашей квадратичной регрессии. Вот пример того, как это сделать:
Квадратичная регрессия была проведена для количественной оценки взаимосвязи между количеством часов, отработанных человеком, и соответствующим ему уровнем счастья (измеряется от 0 до 100). Для анализа использовалась выборка из 16 человек.
Результаты показали, что существует статистически значимая связь между объясняющими переменными часами и часами 2 и переменной счастья (F (2, 13) = 65,095, p < 0,000).
Вместе эти две объясняющие переменные объясняют 90,9% изменчивости счастья.
Уравнение регрессии оказалось таким:
Предполагаемый уровень счастья = -30,253 + 7,173 (часы) – 0,107 (часы 2 )