Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между несколькими независимыми переменными и переменной отклика.
К сожалению, одна проблема, которая часто возникает при регрессии, известна как гетероскедастичность , при которой происходит систематическое изменение дисперсии остатков в диапазоне измеренных значений.
Это приводит к увеличению дисперсии оценок коэффициента регрессии, но регрессионная модель этого не учитывает. Это повышает вероятность того, что регрессионная модель объявит термин в модели статистически значимым, хотя на самом деле это не так.
Одним из способов решения этой проблемы является использование надежных стандартных ошибок , которые более «устойчивы» к проблеме гетероскедастичности и, как правило, обеспечивают более точное измерение истинной стандартной ошибки коэффициента регрессии.
В этом руководстве объясняется, как использовать надежные стандартные ошибки в регрессионном анализе в Stata.
Пример: Надежные стандартные ошибки в Stata
Мы будем использовать встроенный автоматический набор данных Stata, чтобы проиллюстрировать, как использовать надежные стандартные ошибки в регрессии.
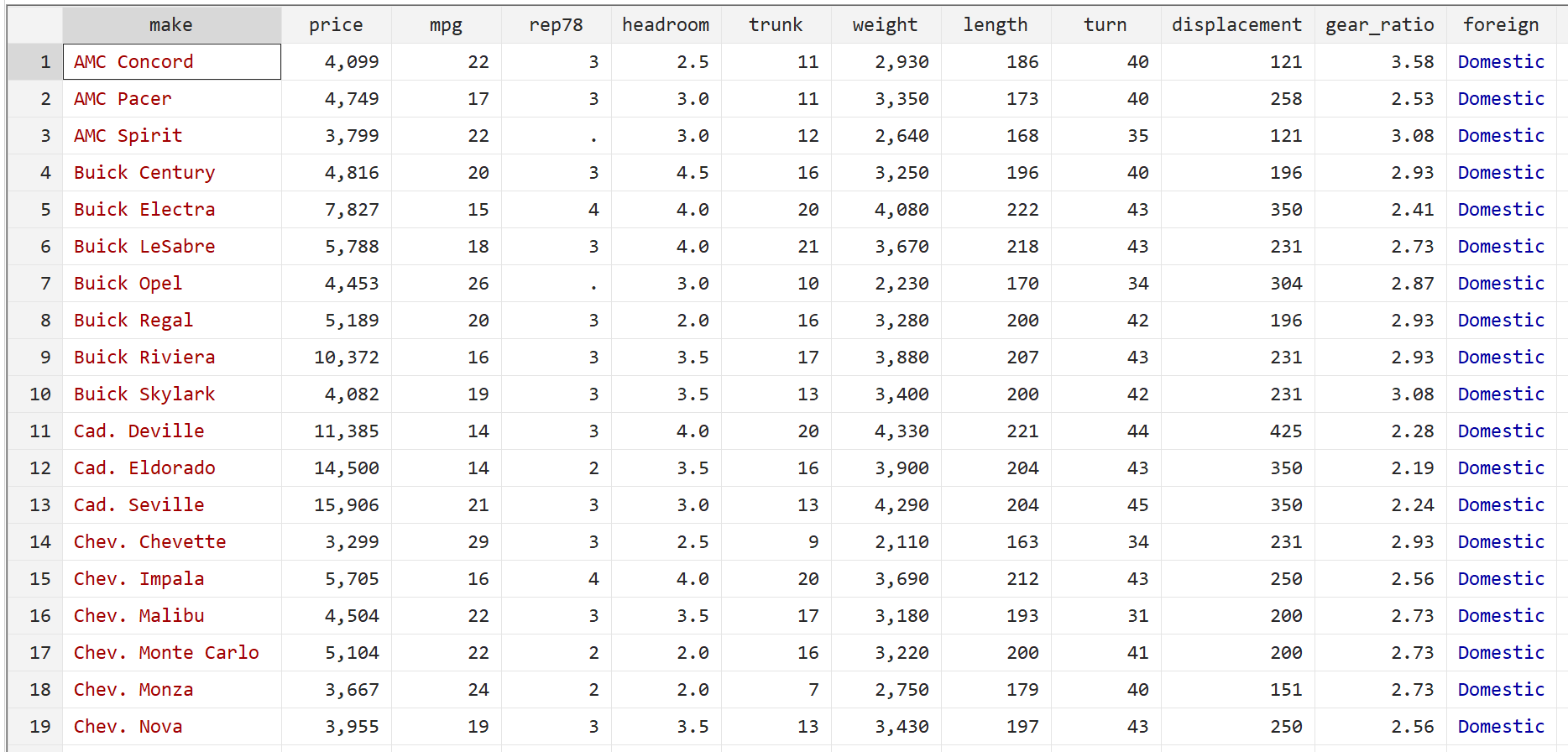
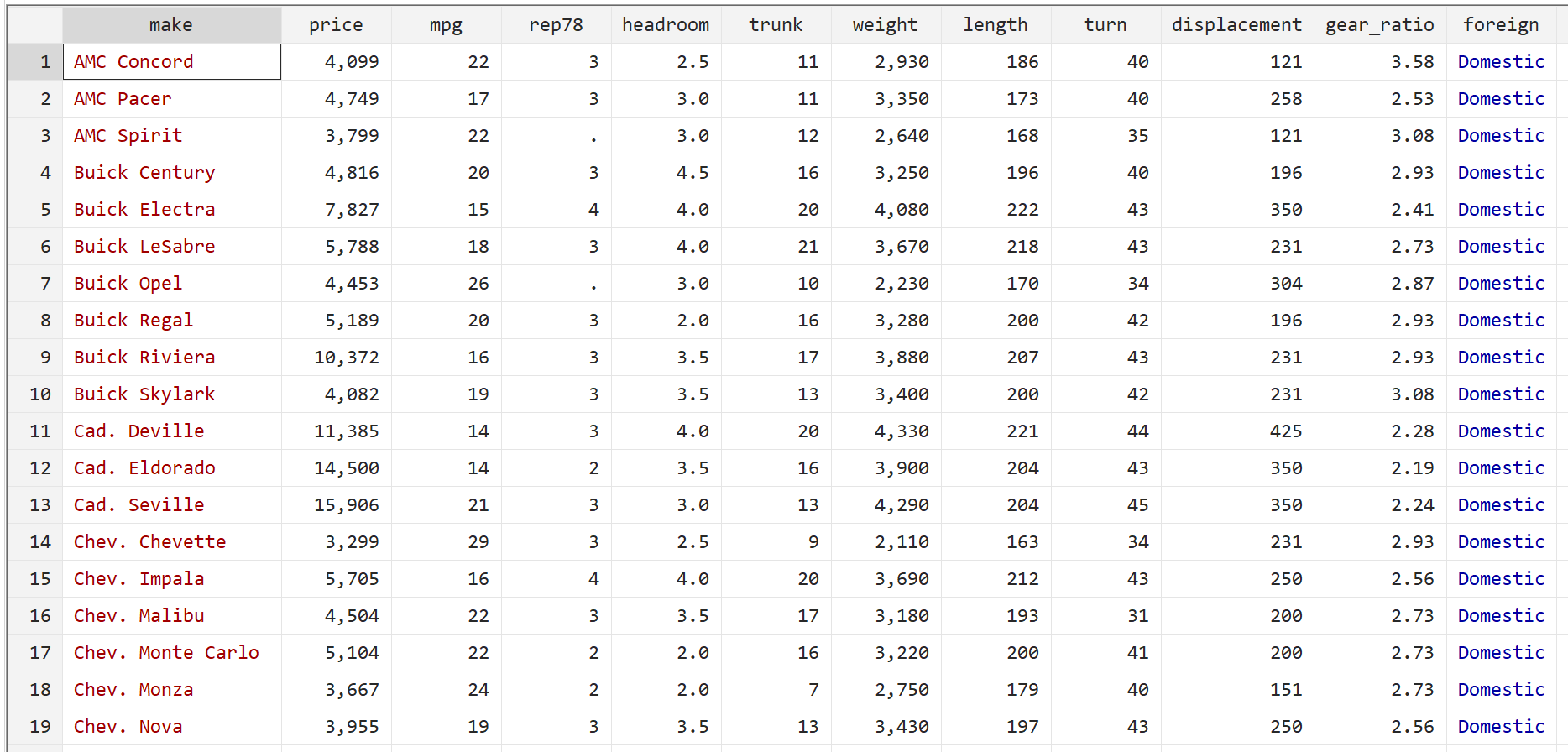
Шаг 1: Загрузите и просмотрите данные.
Сначала используйте следующую команду для загрузки данных:
сисус авто
Затем просмотрите необработанные данные с помощью следующей команды:
бр
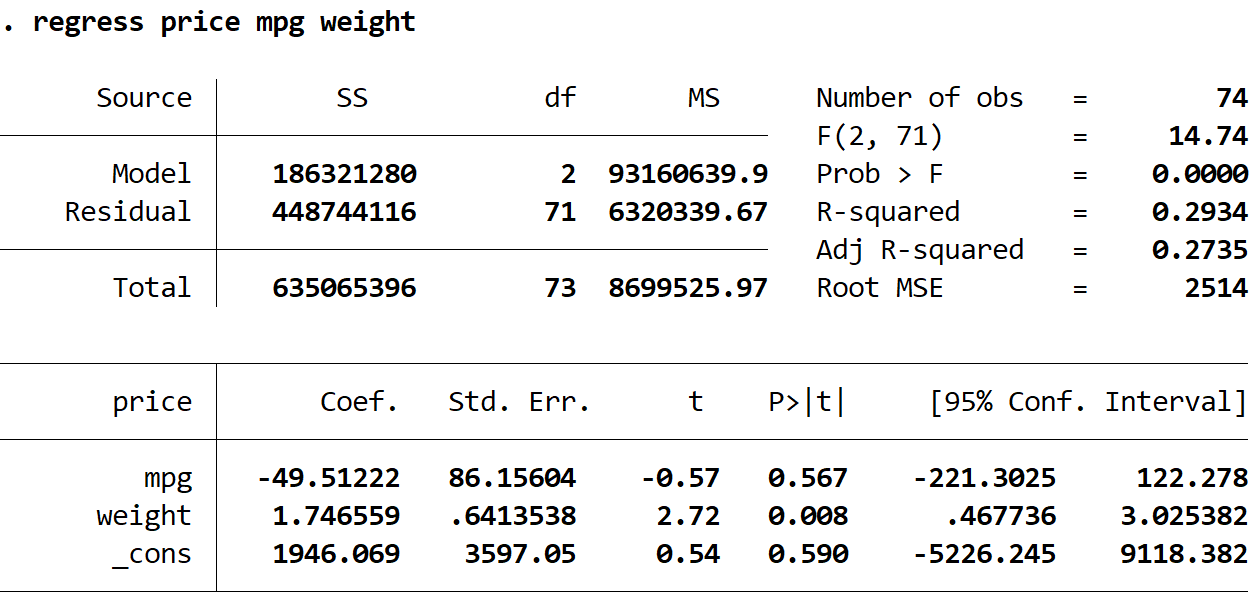
Шаг 2. Выполните множественную линейную регрессию без надежных стандартных ошибок.
Затем мы введем следующую команду, чтобы выполнить множественную линейную регрессию, используя цену в качестве переменной ответа, а мили на галлон и вес в качестве независимых переменных:
регресс цена миль на галлон вес
Шаг 3: Выполните множественную линейную регрессию, используя надежные стандартные ошибки.
Теперь мы выполним точно такую же множественную линейную регрессию, но на этот раз мы будем использовать команду vce(робаст) , чтобы Stata знала, что нужно использовать надежные стандартные ошибки:
регресс цена миль на галлон вес, vce(надежный)
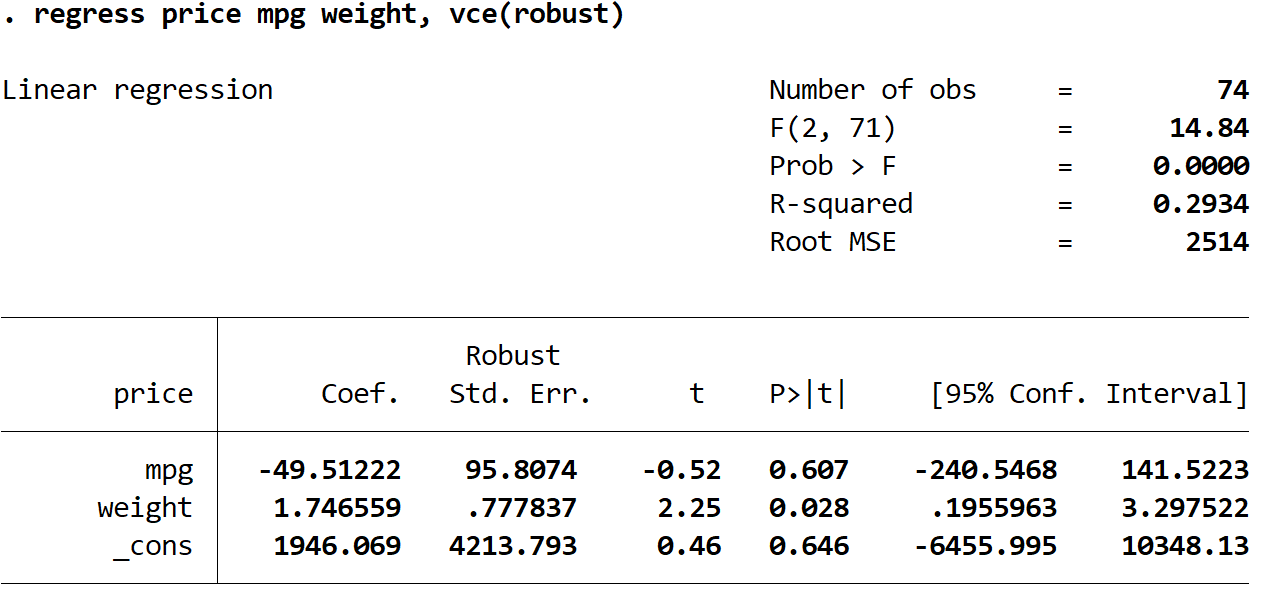
Здесь следует отметить несколько интересных вещей:
1. Оценки коэффициентов остались прежними.Когда мы используем надежные стандартные ошибки, оценки коэффициентов вообще не меняются. Обратите внимание, что оценки коэффициентов для миль на галлон, веса и константы для обеих регрессий следующие:
- миль на галлон: -49,51222
- вес: 1.746559
- _cons: 1946.069
2. Изменены стандартные ошибки.Обратите внимание, что когда мы использовали надежные стандартные ошибки, стандартные ошибки для каждой из оценок коэффициентов увеличивались.
Примечание. В большинстве случаев устойчивые стандартные ошибки будут больше, чем обычные стандартные ошибки, но в редких случаях устойчивые стандартные ошибки могут быть меньше.
3. Изменилась тестовая статистика каждого коэффициента. Обратите внимание, что абсолютное значение каждой тестовой статистики t уменьшилось. Это связано с тем, что статистика теста рассчитывается как оценочный коэффициент, деленный на стандартную ошибку. Таким образом, чем больше стандартная ошибка, тем меньше абсолютное значение тестовой статистики.
4. Изменились p-значения.Обратите внимание, что p-значения для каждой переменной также увеличились. Это связано с тем, что меньшая тестовая статистика связана с большими p-значениями.
Хотя p-значения для наших коэффициентов изменились, переменная mpg по-прежнему не является статистически значимой при α = 0,05, а вес переменной по-прежнему статистически значим при α = 0,05.