Однофакторный дисперсионный анализ используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп.
Если общее значение p из таблицы ANOVA меньше некоторого уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из средних значений групп отличается от других.
Однако это не говорит нам, какие группы отличаются друг от друга. Это просто говорит нам, что не все средние группы равны.
Чтобы выяснить, какие именно группы отличаются друг от друга, мы должны провестиапостериорный тест , способный контролировать частоту ошибок в отношении семьи .
Одним из наиболее часто используемых апостериорных тестов является тест Шеффе.
В этом руководстве объясняется, как выполнить тест Шеффе в R.
Пример: тест Шеффе в R
Предположим, учитель хочет знать, приводят ли три разных метода обучения к разным экзаменационным баллам у студентов. Чтобы проверить это, она случайным образом назначает 10 студентов для использования каждого метода обучения и записывает их экзаменационные баллы.
Мы можем использовать следующие шаги в R, чтобы подобрать однофакторный дисперсионный анализ для проверки различий в средних результатах экзаменов среди трех групп, и использовать тест Шеффе, чтобы точно определить, какие группы отличаются.
Шаг 1: Создайте набор данных.
В следующем коде показано, как создать набор данных, содержащий результаты экзаменов для всех 30 учащихся:
#create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
77, 78, 79, 88, 89, 90, 91, 95, 95, 98))
#view first six rows of data frame
head(data)
technique score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82
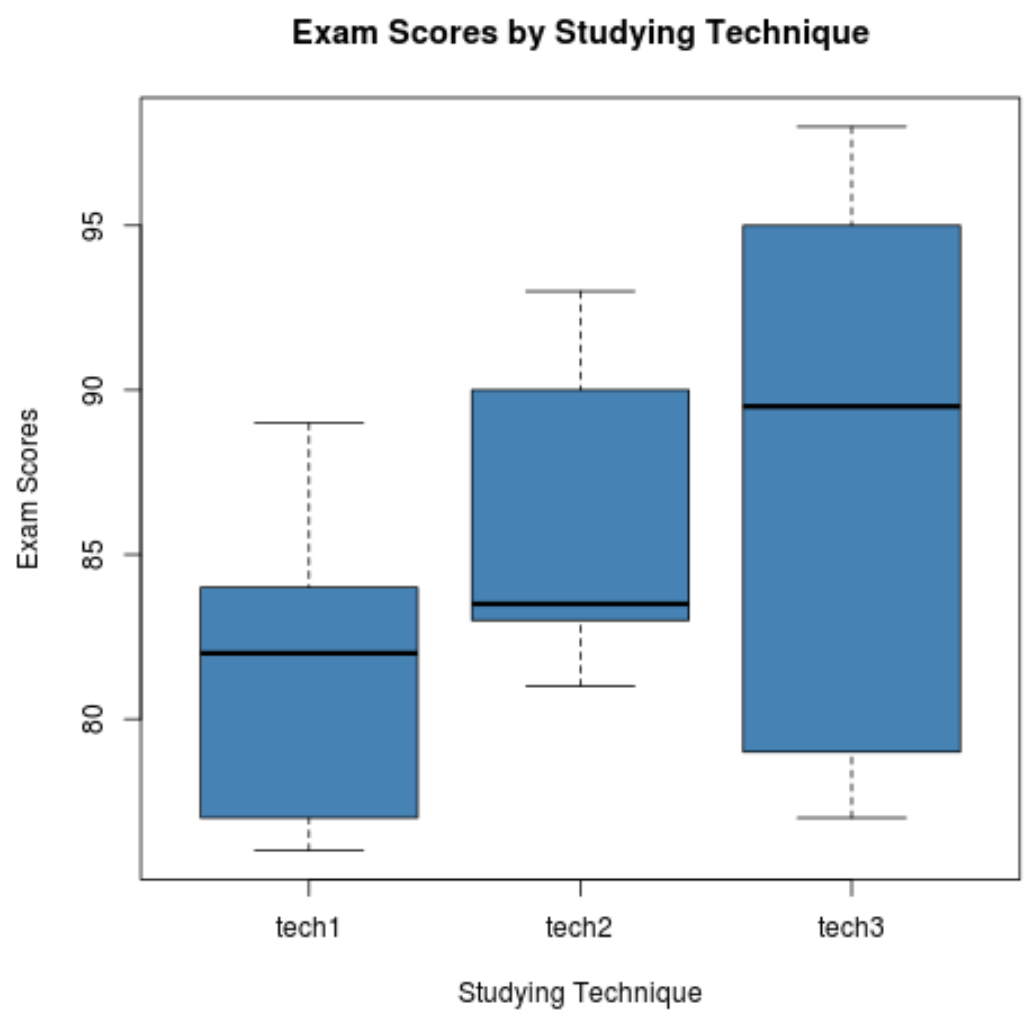
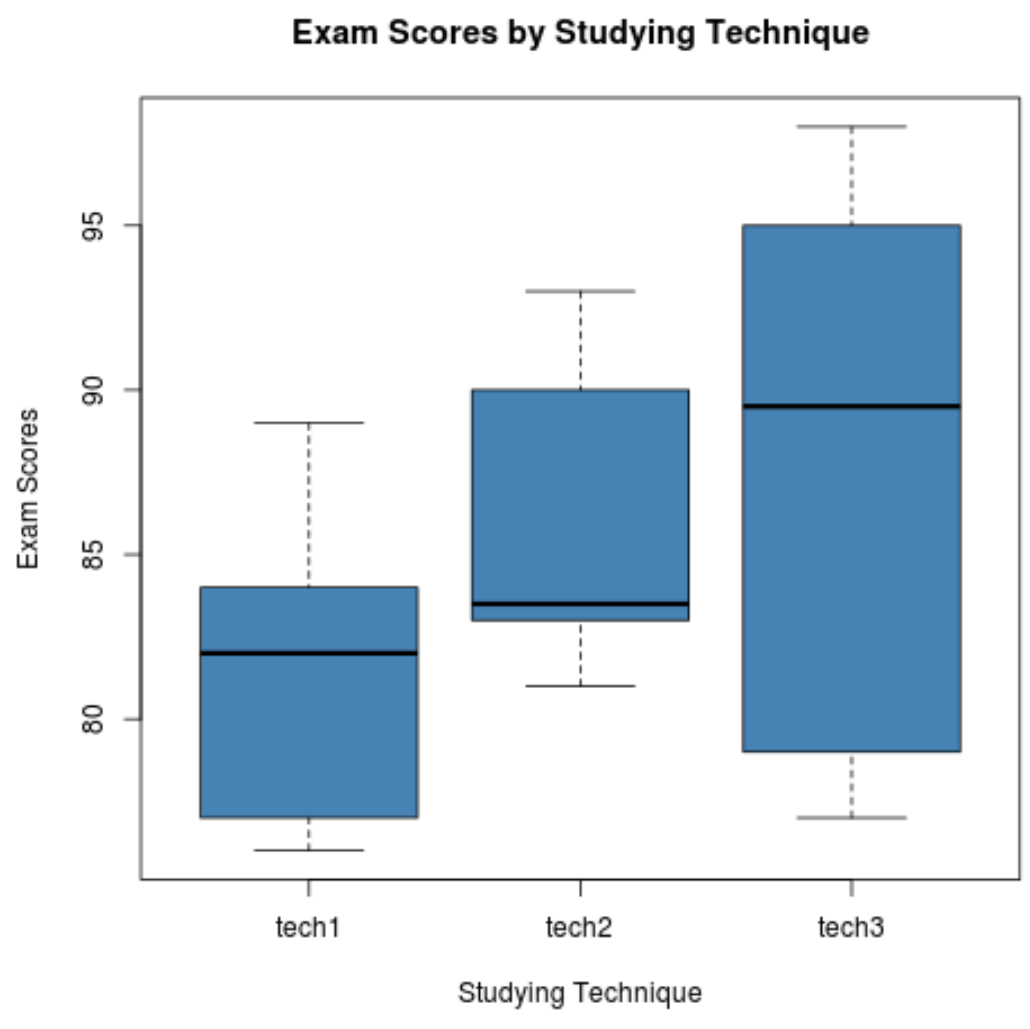
Шаг 2: Визуализируйте результаты экзаменов для каждой группы.
В следующем коде показано, как создавать диаграммы для визуализации распределения баллов по экзаменам для каждой группы:
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
Шаг 3: Выполните односторонний ANOVA.
В следующем коде показано, как выполнить однофакторный дисперсионный анализ для проверки различий между средними баллами за экзамен в каждой группе:
#fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)
#view model output
summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
technique 2 211.5 105.73 3.415 0.0476 \*
Residuals 27 836.0 30.96
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Поскольку общее p-значение ( 0,0476 ) меньше 0,05, это указывает на то, что у каждой группы разные средние баллы за экзамен.
Далее мы проведем тест Шеффе, чтобы определить, какие группы отличаются.
Шаг 4: Проведите тест Шеффе.
Для выполнения теста Шеффе мы будем использовать функцию ScheffeTest() из пакета DescTools .
Следующий код показывает, как использовать эту функцию для нашего примера:
#load DescTools package
library(DescTools)
#perform Scheffe's test
ScheffeTest(model)
Posthoc multiple comparisons of means : Scheffe Test
95% family-wise confidence level
$technique
diff lwr.ci upr.ci pval
tech2-tech1 4.2 -2.24527202 10.645272 0.2582
tech3-tech1 6.4 -0.04527202 12.845272 0.0519.
tech3-tech2 2.2 -4.24527202 8.645272 0.6803
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Способ интерпретации вывода следующий:
- Средняя разница в экзаменационных баллах между техникой 2 и техникой 1 составляет 4,2.Соответствующее значение p для средней разницы составляет 0,2582 .
- Средняя разница в экзаменационных баллах между техникой 3 и техникой 1 составляет 6,4.Соответствующее значение p для средней разницы равно 0,0519 .
- Средняя разница в экзаменационных баллах между техникой 3 и техникой 2 составляет 2,2.Соответствующее значение p для средней разницы равно 0,6803 .
В зависимости от уровня значимости, который мы решили использовать, единственные две группы, которые кажутся статистически значимыми, — это метод 3 и метод 1.
Дополнительные ресурсы
Как провести односторонний дисперсионный анализ в R
Как выполнить тест Тьюки в R
Как выполнить поправку Бонферрони в R