Простая линейная регрессия — это метод, который можно использовать для понимания взаимосвязи между независимой переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Stata.
Пример: простая линейная регрессия в Stata
Предположим, нам интересно понять взаимосвязь между весом автомобиля и его милями на галлон. Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя вес в качестве независимой переменной и мили на галлон в качестве переменной отклика.
Выполните следующие шаги в Stata, чтобы провести простую линейную регрессию с использованием набора данных auto , который содержит данные о 74 различных автомобилях.
Шаг 1: Загрузите данные.
Загрузите данные, введя следующее в поле Command:
используйте http://www.stata-press.com/data/r13/auto
Шаг 2: Получите сводку данных.
Чтобы быстро понять данные, с которыми вы работаете, введите следующее в поле «Команда»:
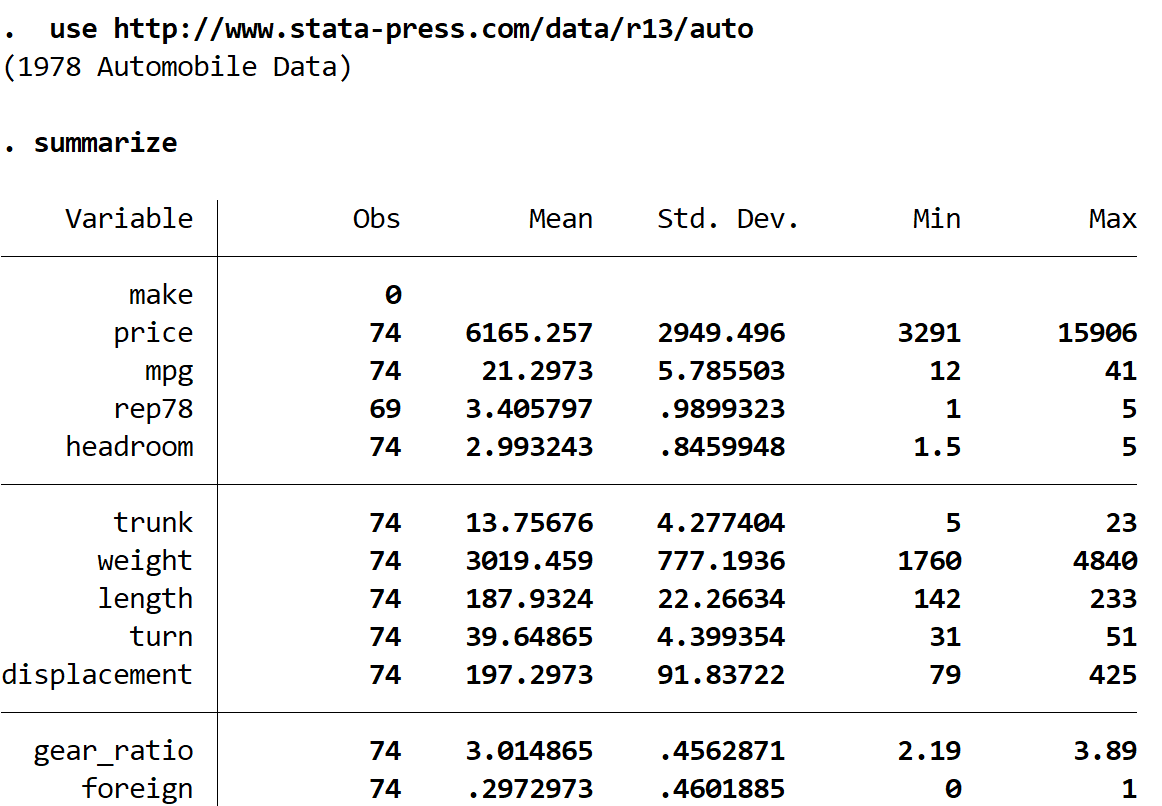
подвести итог
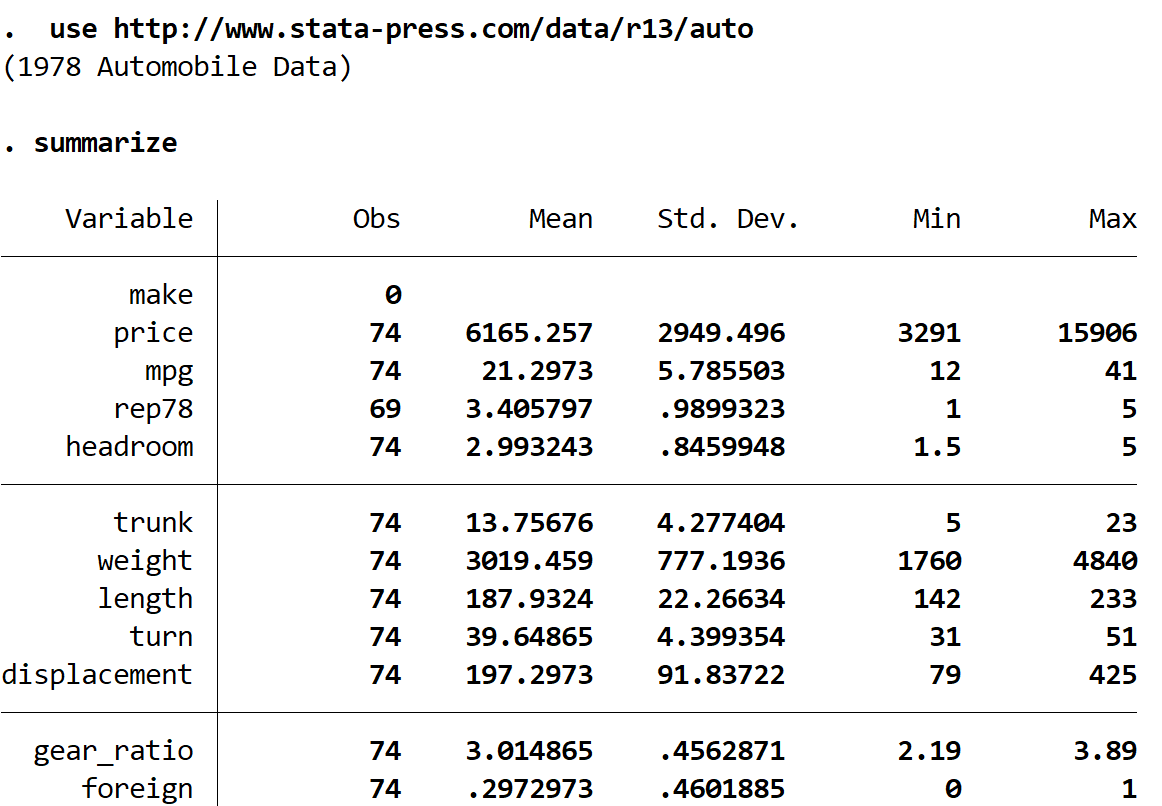
Мы видим, что в наборе данных есть 12 различных переменных, но нас интересуют только две из них: mpg и weight .
Шаг 3: Визуализируйте данные.
Прежде чем мы выполним простую линейную регрессию, давайте сначала создадим диаграмму рассеяния веса по сравнению с милями на галлон, чтобы мы могли визуализировать взаимосвязь между этими двумя переменными и проверить наличие каких-либо очевидных выбросов. Введите следующее в поле «Команда», чтобы создать диаграмму рассеяния:
разброс веса на галлон
Получается следующая диаграмма рассеяния:
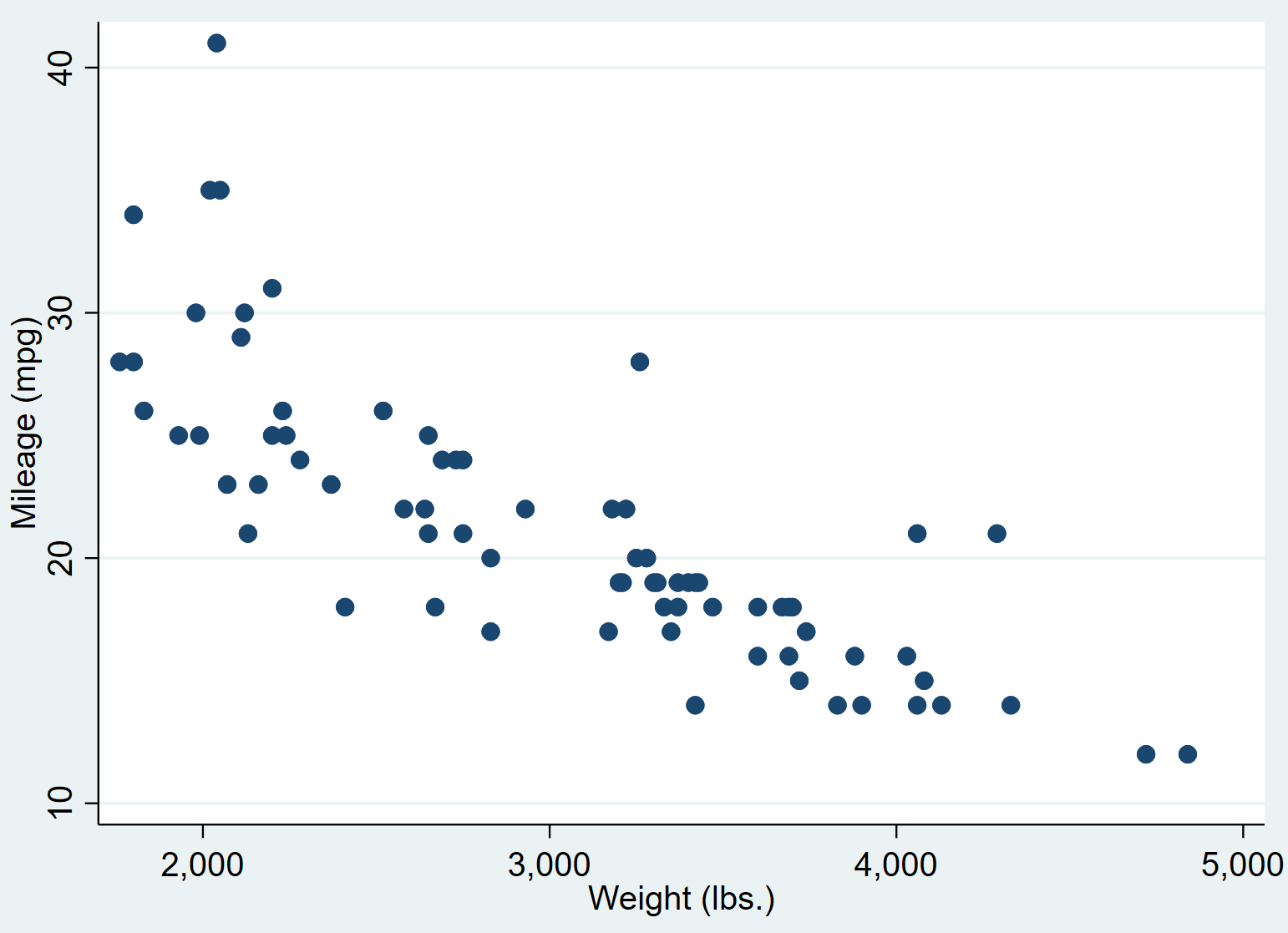
Мы можем видеть, что автомобили с более высоким весом, как правило, имеют меньше миль на галлон. Чтобы количественно оценить эту связь, мы теперь выполним простую линейную регрессию.
Шаг 4: Выполните простую линейную регрессию.
Введите следующее в поле «Команда», чтобы выполнить простую линейную регрессию с использованием веса в качестве независимой переменной и миль на галлон в качестве переменной отклика.
регресс веса миль на галлон
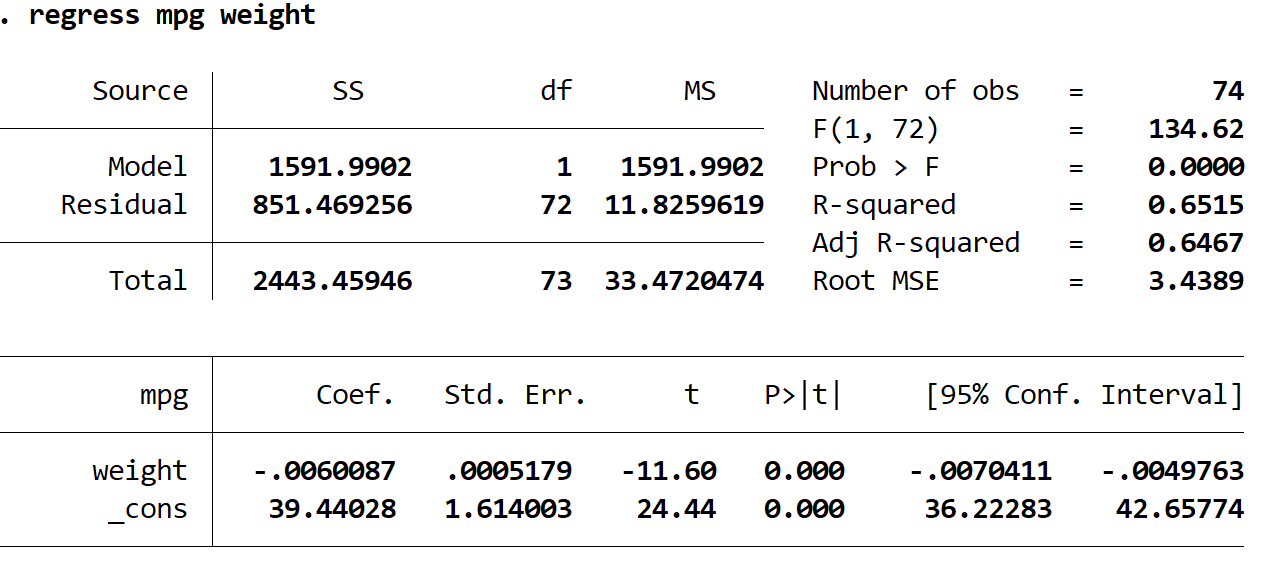
Вот как интерпретировать наиболее интересные числа в выводе:
R-квадрат: 0,6515. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 65,15% вариации миль на галлон можно объяснить весом.
Коэф (вес): -0,006. Это говорит нам о среднем изменении переменной отклика, связанном с увеличением на одну единицу объясняющей переменной. В этом примере увеличение веса на каждый фунт связано с уменьшением в среднем на 0,006 миль на галлон.
Коэффициент (_cons): 39,44028. Это говорит нам о среднем значении переменной отклика, когда независимая переменная равна нулю. В этом примере средний расход составляет 39,44028 миль на галлон, когда вес автомобиля равен нулю. На самом деле это не имеет особого смысла интерпретировать, поскольку вес автомобиля не может быть равен нулю, но число 39,44028 необходимо для формирования уравнения регрессии.
Р>|т| (вес): 0,000. Это p-значение, связанное со статистикой теста для веса. В этом случае, поскольку это значение меньше 0,05, мы можем заключить, что существует статистически значимая связь между весом и милями на галлон.
Уравнение регрессии. Наконец, мы можем составить уравнение регрессии, используя два значения коэффициента. В этом случае уравнение будет таким:
прогнозируемый миль на галлон = 39,44028 - 0,0060087 * (вес)
Мы можем использовать это уравнение, чтобы найти прогнозируемый расход автомобиля, учитывая его вес. Например, прогнозируется, что автомобиль весом 4000 фунтов расходует 15,405 миль на галлон:
расчетные мили на галлон = 39,44028 – 0,0060087*(4000) = 15,405
Шаг 5: Сообщите о результатах.
Наконец, мы хотим сообщить о результатах нашей простой линейной регрессии. Вот пример того, как это сделать:
Линейная регрессия была выполнена для количественной оценки взаимосвязи между весом автомобиля и количеством миль на галлон. Для анализа использовалась выборка из 74 автомобилей.
Результаты показали, что существует статистически значимая взаимосвязь между весом и милями на галлон (t = -11,60, p <0,0001), а на вес приходится 65,15% объясненной изменчивости миль на галлон.
Уравнение регрессии оказалось таким:
прогнозируемый миль на галлон = 39,44 - 0,006 (вес)
Каждый дополнительный фунт был связан со снижением в среднем на -0,006 миль на галлон.