Индекс разнообразия Симпсона — это способ измерения разнообразия видов в сообществе.
Обозначается как D , этот индекс рассчитывается как:
D = Σn i (n i -1) / N (N-1)
куда:
- n i : количество организмов, принадлежащих к виду i .
- N: общее количество организмов
Значение индекса разнообразия Симпсона находится в диапазоне от 0 до 1. Чем выше значение, тем меньше разнообразие.
Поскольку эта интерпретация несколько противоречит здравому смыслу, мы часто рассчитываем индекс разнообразия Симпсона (иногда называемый индексом доминирования), который рассчитывается как 1 – D. Чем выше значение этого индекса, тем выше разнообразие видов.
Мы также можем рассчитать обратный индекс Симпсона , который рассчитывается как 1/D. Наименьшее значение этого индекса равно 1, а наибольшее значение равно количеству видов.
Например, если имеется 7 различных видов, то максимальное значение этого индекса будет равно 7. Чем выше значение этого индекса, тем больше разнообразие видов.
В следующем пошаговом примере показано, как рассчитать эти различные индексы для данного сообщества.
Шаг 1: Соберите данные
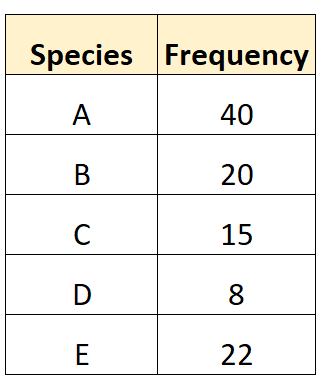
Предположим, биолог хочет измерить разнообразие видов в местном лесу. Она собирает следующие данные:
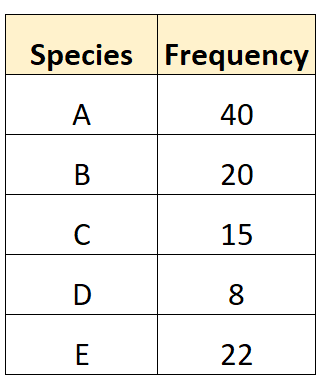
Шаг 2: вычислить N
Далее она может подсчитать общее количество организмов.

Всего 105 органов.
Шаг 3: Рассчитать n i (n i -1)
Далее она может вычислить n i (n i -1). Например, первый вид будет рассчитан как 40*(40-1) = 1560. Она может повторить этот расчет для каждого вида:

Шаг 4: Рассчитайте индекс разнообразия Симпсона
Наконец, мы можем использовать следующую формулу для расчета индекса Симпсона:
D = Σn i (n i -1) / N (N-1)
Используя значения, которые мы нашли ранее, индекс Симпсона можно рассчитать как:
D = 2668/(105*(105-1)) = 0,244 .
Мы также можем рассчитать индекс разнообразия Симпсона как 1 – D = 1 – 0,244 = 0,756 .
Мы также можем рассчитать обратный индекс Симпсона как 1 / D = 1 / 0,244 = 4,09 .
Дополнительные ресурсы
Не стесняйтесь использовать этот калькулятор индекса разнообразия Симпсона для автоматического расчета индекса разнообразия Симпсона для любого набора данных.