В статистике корреляция относится к силе и направлению связи между двумя переменными. Значение коэффициента корреляции может варьироваться от -1 до 1 со следующими интерпретациями:
- -1: идеальная отрицательная связь между двумя переменными
- 0: нет связи между двумя переменными
- 1: идеальная положительная связь между двумя переменными
Один особый тип корреляции называется ранговой корреляцией Спирмена и используется для измерения корреляции между двумя ранжированными переменными. (например, оценка балла учащегося на экзамене по математике и оценка его оценки на экзамене по естественным наукам в классе).
В этом руководстве объясняется, как рассчитать ранговую корреляцию Спирмена между двумя переменными в Excel.
Пример: ранговая корреляция Спирмена в Excel
Выполните следующие шаги, чтобы вычислить ранговую корреляцию Спирмена между результатами экзамена по математике и результатами экзамена по естественным наукам 10 учащихся в определенном классе.
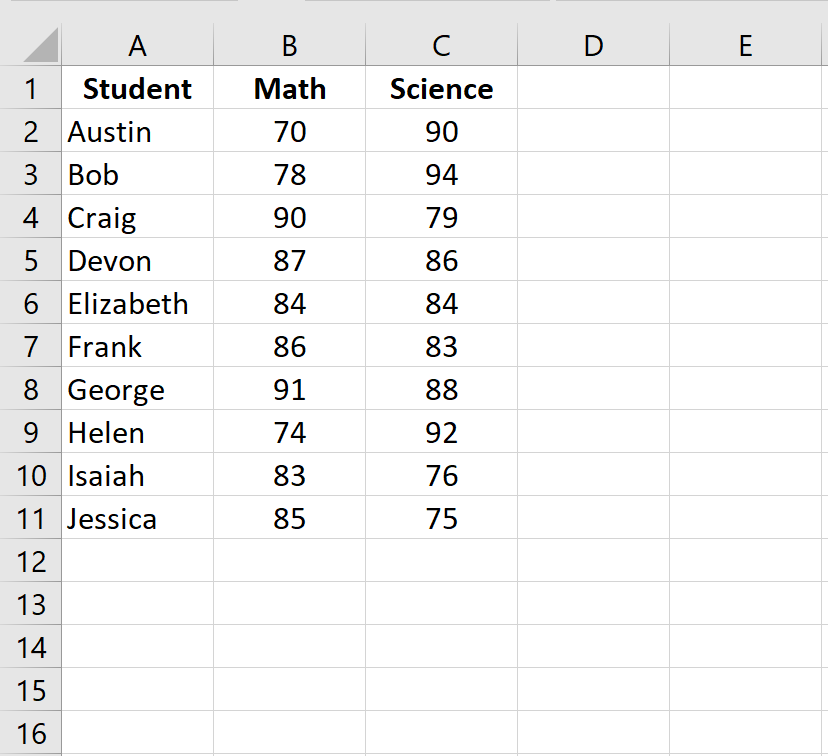
Шаг 1: Введите данные.
Введите экзаменационные баллы для каждого учащегося в два отдельных столбца:
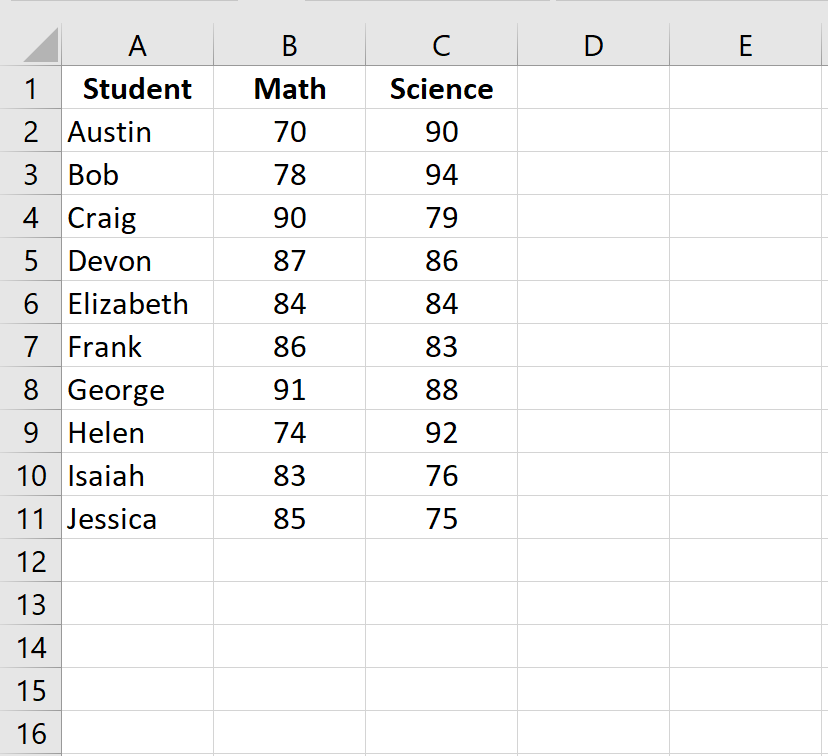
Шаг 2: Рассчитайте ранги для каждого экзаменационного балла.
Далее мы рассчитаем рейтинг для каждого экзаменационного балла. Используйте следующие формулы в ячейках D2 и E2, чтобы вычислить рейтинги по математике и естественным наукам для первого ученика, Остина:
Ячейка D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Ячейка E2: =RANK.AVG(C2, $C$2:$C$11, 0)
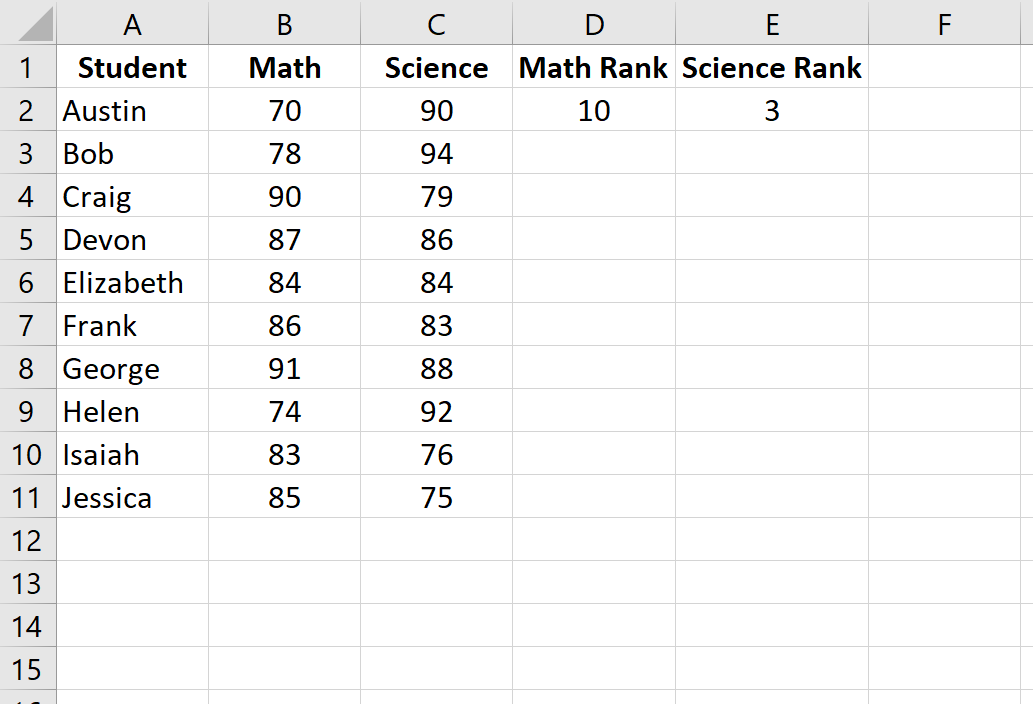
Затем выделите оставшиеся ячейки для заполнения:
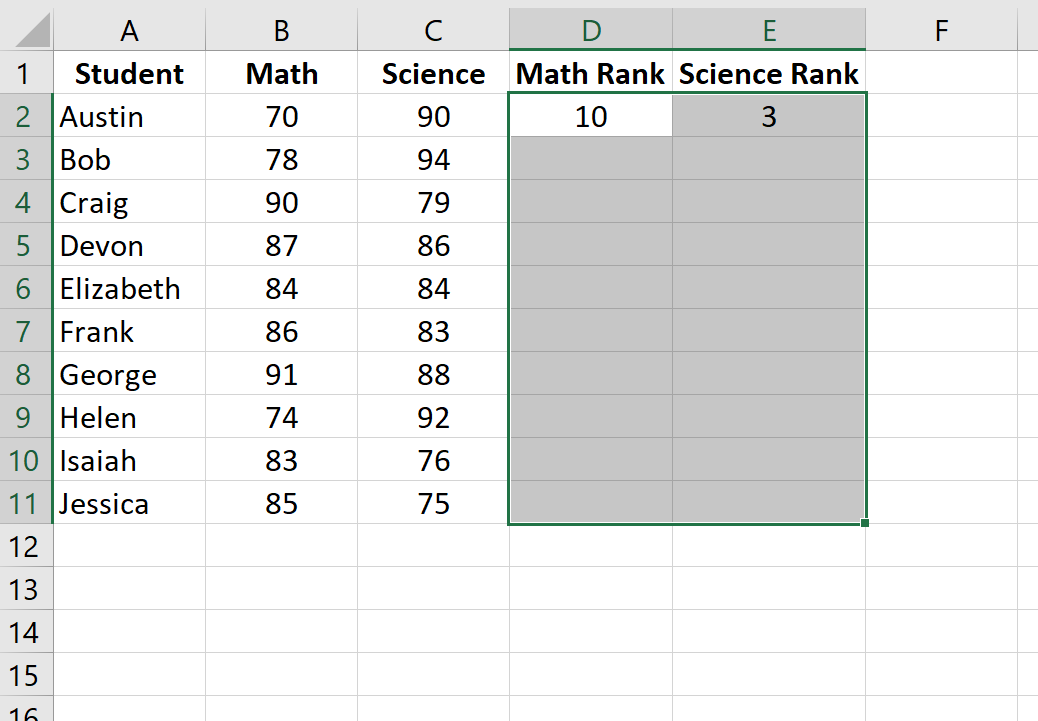
Затем нажмите Ctrl+D, чтобы заполнить ранги для каждого ученика:
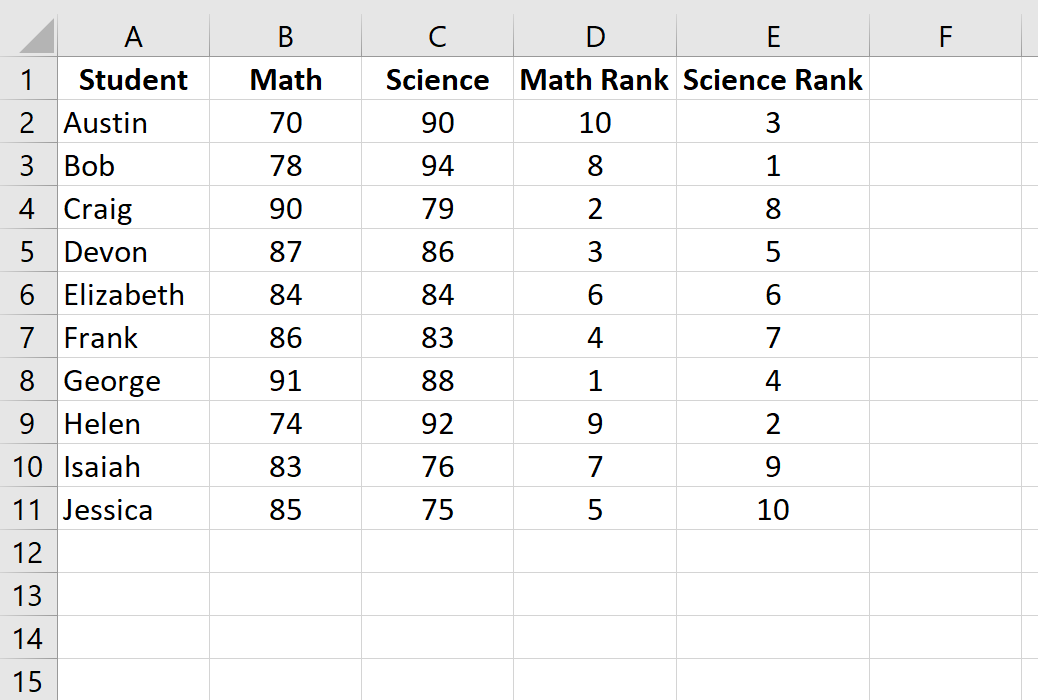
Шаг 3: Рассчитайте коэффициент ранговой корреляции Спирмена.
Наконец, мы рассчитаем коэффициент ранговой корреляции Спирмена между оценками по математике и по естественным наукам с помощью функции CORREL() :
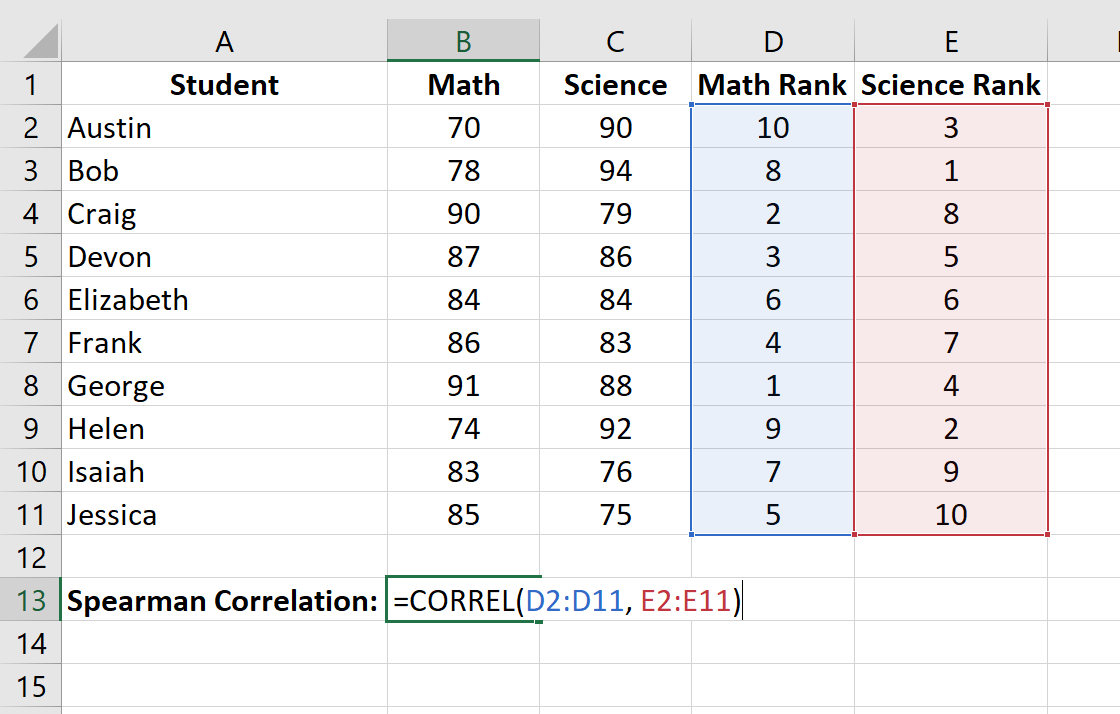
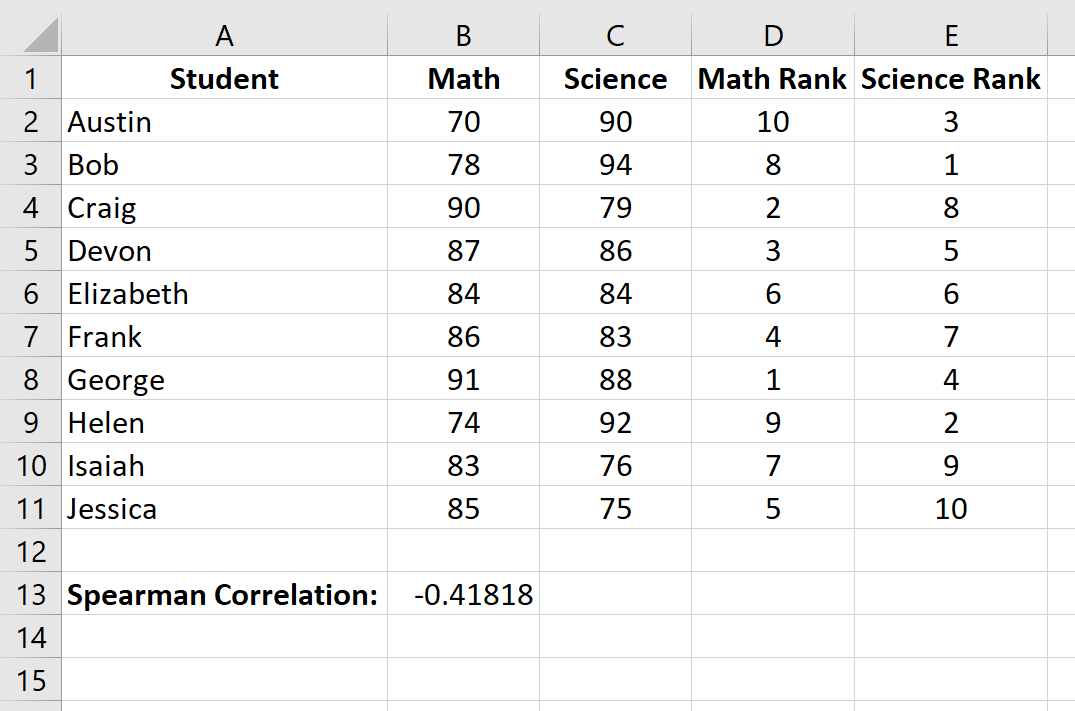
Ранговая корреляция Спирмена оказывается равной -0,41818 .
Шаг 4 (необязательно): Определите, является ли ранговая корреляция Спирмена статистически значимой.
На предыдущем шаге мы обнаружили, что ранговая корреляция Спирмена между результатами экзаменов по математике и естественным наукам составляет -0,41818 , что указывает на отрицательную корреляцию между двумя переменными.
Однако, чтобы определить, является ли эта корреляция статистически значимой, нам нужно будет обратиться к таблице ранговой корреляции Спирмена критических значений, которая показывает критические значения, связанные с различными размерами выборки (n) и уровнями значимости (α).
Если абсолютное значение нашего коэффициента корреляции больше критического значения в таблице, то корреляция между двумя переменными является статистически значимой.
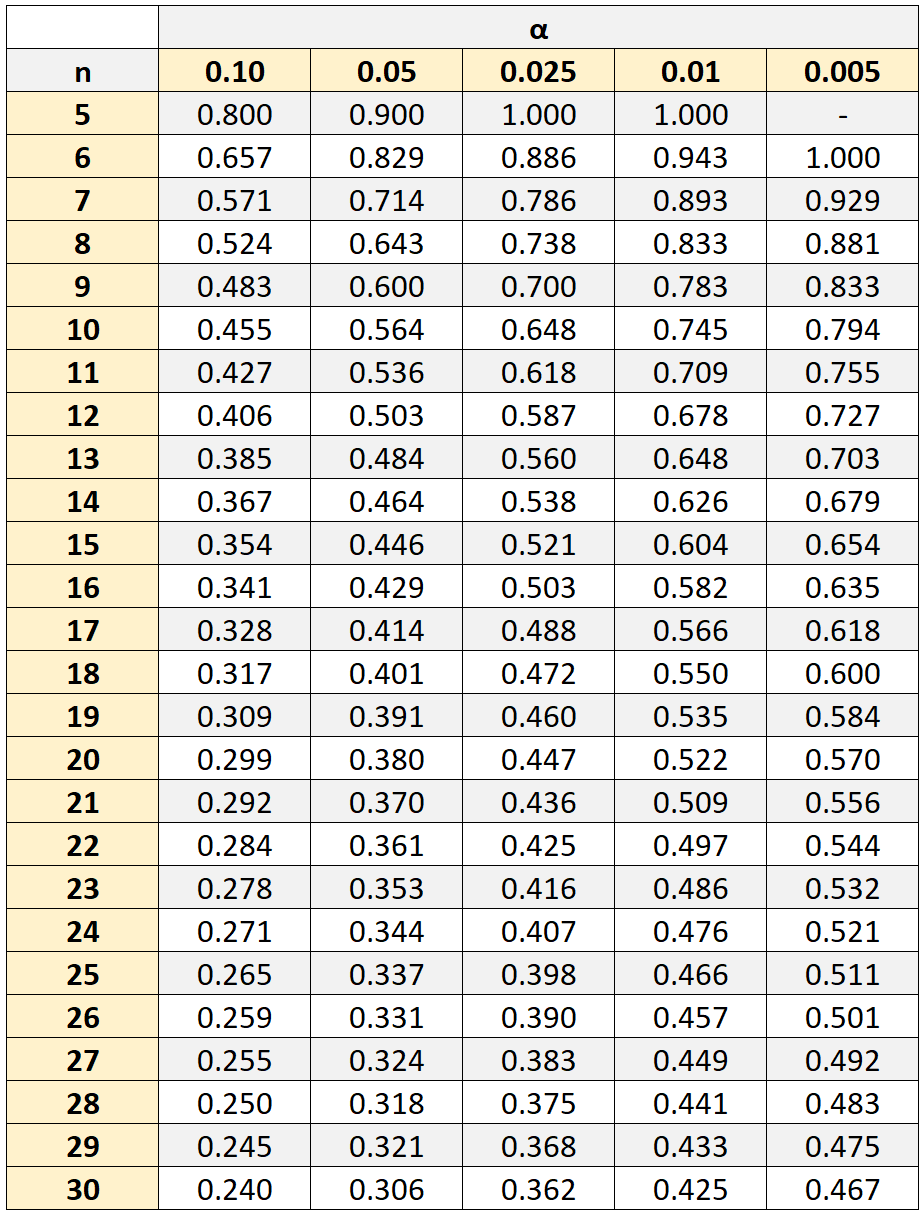
В нашем примере размер выборки составлял n = 10 студентов. Используя уровень значимости 0,05, мы находим, что критическое значение равно 0,564 .
Поскольку рассчитанное нами абсолютное значение рангового коэффициента корреляции Спирмена ( 0,41818 ) не превышает этого критического значения, это означает, что корреляция между баллами по математике и естественным наукам не является статистически значимой.