Стандартизация и нормализация — это два способа масштабирования данных.
Стандартизация изменяет масштаб набора данных, чтобы иметь среднее значение 0 и стандартное отклонение 1. Для этого используется следующая формула:
х новый = (х я - х ) / с
куда:
- x i : i -е значение в наборе данных
- x : Среднее значение выборки
- s : Стандартное отклонение выборки
Нормализация масштабирует набор данных таким образом, чтобы каждое значение находилось в диапазоне от 0 до 1. Для этого используется следующая формула:
x новый = (x i – x мин ) / (x макс – x мин )
куда:
- x i : i -е значение в наборе данных
- x min : минимальное значение в наборе данных
- x max : максимальное значение в наборе данных
В следующих примерах показано, как стандартизировать и нормализовать набор данных на практике.
Пример: как стандартизировать данные
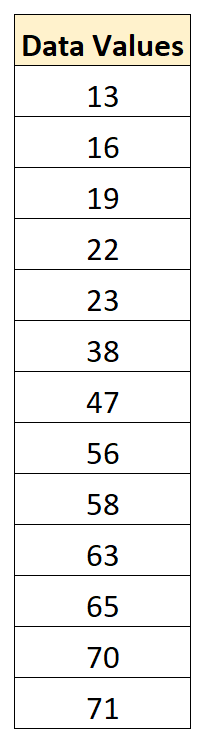
Предположим, у нас есть следующий набор данных:
Среднее значение в наборе данных составляет 43,15, а стандартное отклонение — 22,13.
Чтобы нормализовать первое значение 13 , мы должны применить формулу, которую использовали ранее:
- x новый = (x i - x ) / s = (13 - 43,15) / 22,13 = -1,36
Чтобы нормализовать второе значение 16 , мы будем использовать ту же формулу:
- x новый = (x i - x ) / s = (16 - 43,15) / 22,13 = -1,23
Чтобы нормализовать третье значение 19 , мы будем использовать ту же формулу:
- x новый = (x i - x ) / s = (19 - 43,15) / 22,13 = -1,09
Мы можем использовать эту же формулу для стандартизации каждого значения в исходном наборе данных:
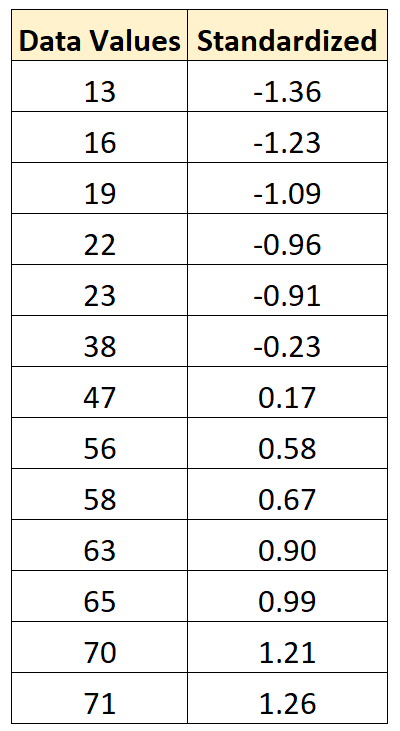
Пример: как нормализовать данные
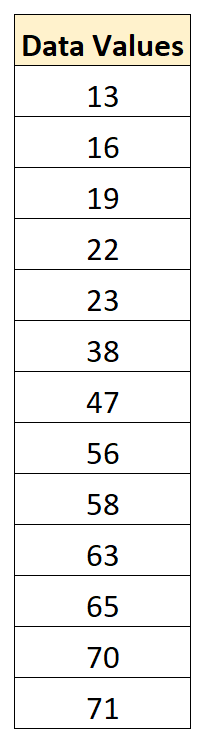
Еще раз предположим, что у нас есть следующий набор данных:

Минимальное значение в наборе данных — 13, максимальное — 71.
Чтобы нормализовать первое значение 13 , мы должны применить формулу, которую использовали ранее:
- x new = (x i – x min ) / (x max – x min ) = (13 – 13) / (71 – 13) = 0
Чтобы нормализовать второе значение 16 , мы будем использовать ту же формулу:
- x new = (x i – x min ) / (x max – x min ) = (16 – 13) / (71 – 13) = 0,0517
Чтобы нормализовать третье значение 19 , мы будем использовать ту же формулу:
- x new = (x i – x min ) / (x max – x min ) = (19 – 13) / (71 – 13) = 0,1034
Мы можем использовать эту же формулу, чтобы нормализовать каждое значение в исходном наборе данных между 0 и 1:
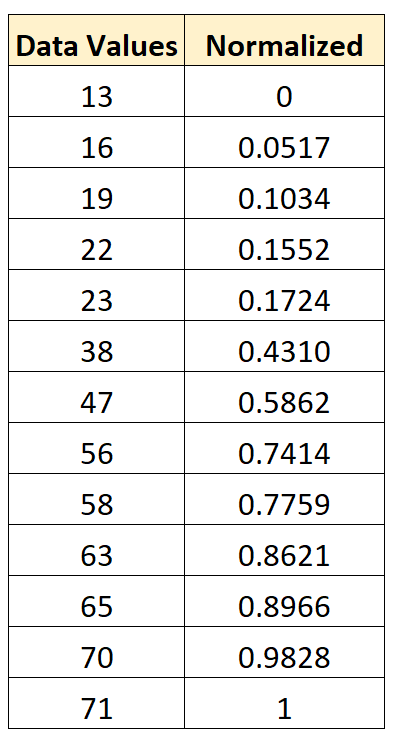
Стандартизация против нормализации: когда использовать каждый
Обычно мы нормализуем данные при выполнении некоторого типа анализа, в котором у нас есть несколько переменных, измеряемых в разных масштабах, и мы хотим, чтобы каждая из переменных имела одинаковый диапазон.
Это предотвращает чрезмерное влияние одной переменной, особенно если она измеряется в разных единицах (например, если одна переменная измеряется в дюймах, а другая — в ярдах).
С другой стороны, мы обычно стандартизируем данные, когда хотим знать, на сколько стандартных отклонений каждое значение в наборе данных отличается от среднего.
Например, у нас может быть список результатов экзаменов для 500 учащихся определенной школы, и мы хотели бы знать, на сколько стандартных отклонений каждый результат экзамена отличается от среднего балла.
В этом случае мы могли бы стандартизировать необработанные данные, чтобы узнать эту информацию. Тогда стандартизированный балл 1,26 говорит нам о том, что экзаменационный балл этого конкретного учащегося на 1,26 стандартного отклонения выше среднего экзаменационного балла.
Если вы решите нормализовать или стандартизировать свои данные, имейте в виду следующее:
- Нормализованный набор данных всегда будет иметь значения в диапазоне от 0 до 1.
- Стандартизированный набор данных будет иметь среднее значение 0 и стандартное отклонение 1, но нет конкретных верхней или нижней границы для максимального и минимального значений.
В зависимости от вашего конкретного сценария может иметь смысл нормализовать или стандартизировать данные.
Дополнительные ресурсы
В следующих руководствах объясняется, как стандартизировать и нормализовать данные в различных статистических программах:
Как нормализовать данные в R
Как нормализовать данные в Excel
Как нормализовать данные в Python
Как стандартизировать данные в R