Станиновая оценка , сокращенно от «стандартной девятки», представляет собой способ масштабирования результатов тестов по стандартной девятибалльной шкале.
Используя этот метод, мы можем преобразовать каждый балл теста из исходного балла (то есть от 0 до 100) в число от 1 до 9.
Мы используем простой двухэтапный процесс для масштабирования тестовых баллов до баллов станина:
1. Проранжируйте баллы каждого теста от самого низкого до самого высокого.
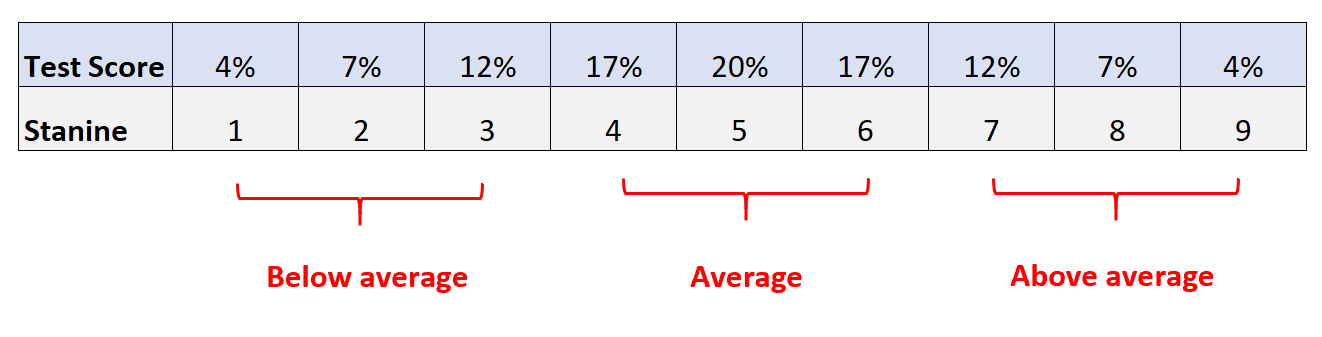
2. Присвойте 4% с наименьшими оценками оценку станину 1, следующим 7% оценок с наименьшим значением — оценку станина 2 и т. д. в соответствии со следующей таблицей:

В целом мы расцениваем результаты тестов следующим образом:
- Станины 1, 2, 3: Ниже среднего
- Станины 4, 5, 6: средние
- Станины 7, 8, 9: выше среднего
Оказывается, стандартная шкала имеет среднее значение пять и стандартное отклонение два.
Плюсы и минусы оценок Stanine
Оценки Stanine предлагают следующие плюсы и минусы:
За : баллы Stanine позволяют нам быстро понять, где находится данный результат теста по сравнению со всеми другими результатами теста.
Например, мы знаем, что учащийся, получивший тестовый балл по станине 5, принадлежит к средним 20% всех тестовых баллов. И мы знаем, что студент, попадающий в станин 9, получил тестовый балл в верхних 4% всех баллов.
Против: недостатком использования станинов является то, что каждый станин не одинакового размера, и результат теста в данном станине может быть ближе к баллам в следующем станине по сравнению с баллами в его собственном станине.
Например, учащиеся, получившие баллы от 40-го до 60-го процентиля, объединяются в группу в группе 5. Однако учащийся, чей результат теста попадает в 58-й процентиль, будет ближе к результатам, полученным в группе 6, по сравнению с большинством оценок. получил в станине 5.
Альтернативы баллам Stanine
Двумя альтернативами станиновым показателям являются процентили и z-показатели.
1. Процентиль сообщает нам процент всех оценок, выше которых находится данный результат теста.
Например, результат теста на 90-м процентиле выше, чем 90% всех результатов теста. Результат теста, попадающий в 50-й процентиль, находится ровно посередине всех результатов теста.
2. Z-оценка говорит нам, сколько стандартных отклонений данной оценки от среднего. Он рассчитывается как:
z = (X - μ) / σ
куда:
- X — это одно необработанное значение данных.
- μ - среднее значение набора данных
- σ - стандартное отклонение набора данных
Мы интерпретируем z-значения следующим образом:
- Положительный z-показатель указывает на то, что результат теста выше среднего.
- Отрицательный z-показатель указывает на то, что результат теста ниже среднего.
- Z-показатель, равный нулю, указывает на то, что результат теста точно равен среднему значению.
Чем дальше z-показатель от нуля, тем дальше данный результат теста от среднего.
Как z-показатели, так и процентили дают нам более точное представление о том, какое место занимают определенные результаты тестов по сравнению со стандартными оценками.


