Критерий Стьюдента Уэлча используется для сравнения средних между двумя независимыми группами, когда не предполагается, что эти две группы имеют равные отклонения.
Чтобы выполнить t-критерий Уэлча в R, мы можем использовать функцию t.test() , которая использует следующий синтаксис:
t.test(x, y, альтернатива = c("двусторонний", "меньше", "больше"))
куда:
- x: числовой вектор значений данных для первой группы.
- y: числовой вектор значений данных для второй группы.
- альтернатива: Альтернативная гипотеза теста. По умолчанию двусторонний.
В следующем примере показано, как использовать эту функцию для выполнения t-критерия Уэлча в R.
Пример: t-критерий Уэлча в R
Учитель хочет сравнить результаты экзаменов 12 учеников, которые использовали буклет для подготовки к экзамену, и 12 учеников, которые этого не сделали.
Следующие векторы показывают экзаменационные баллы для студентов в каждой группе:
booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)
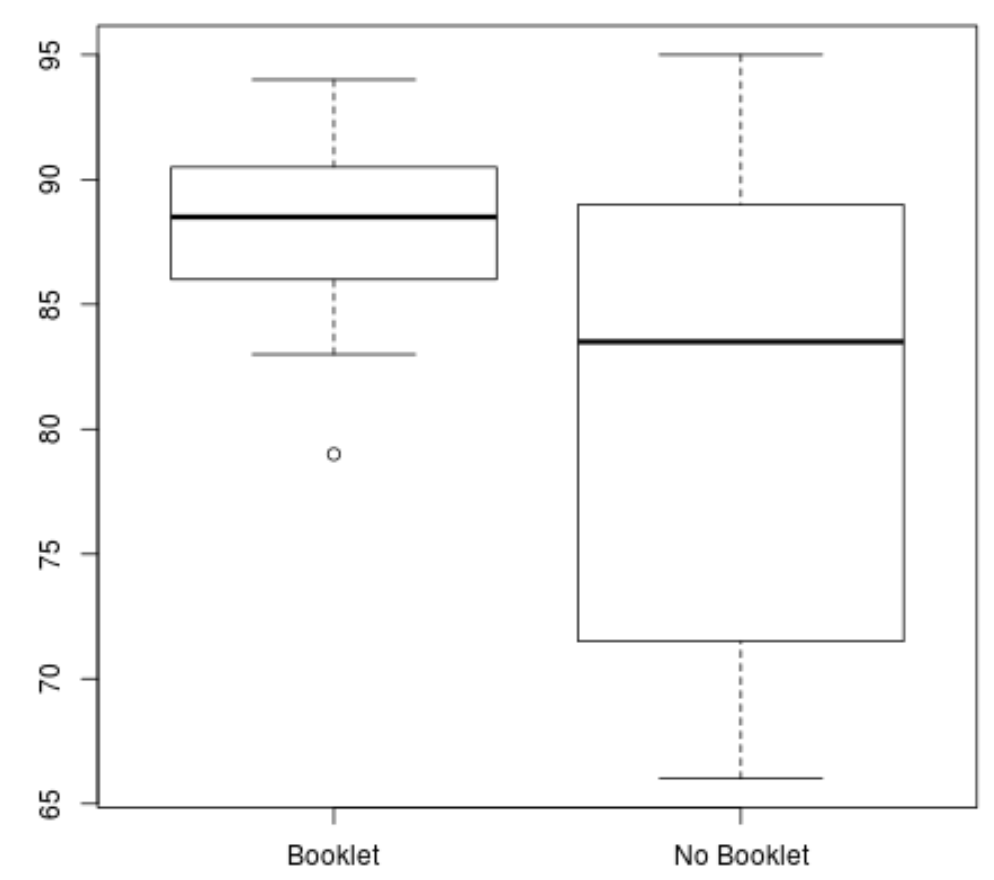
Прежде чем мы выполним t-критерий Уэлча, мы можем сначала создать блок -диаграммы, чтобы визуализировать распределение баллов для каждой группы:
boxplot(booklet, no_booklet, names =c(" Booklet"," No Booklet "))
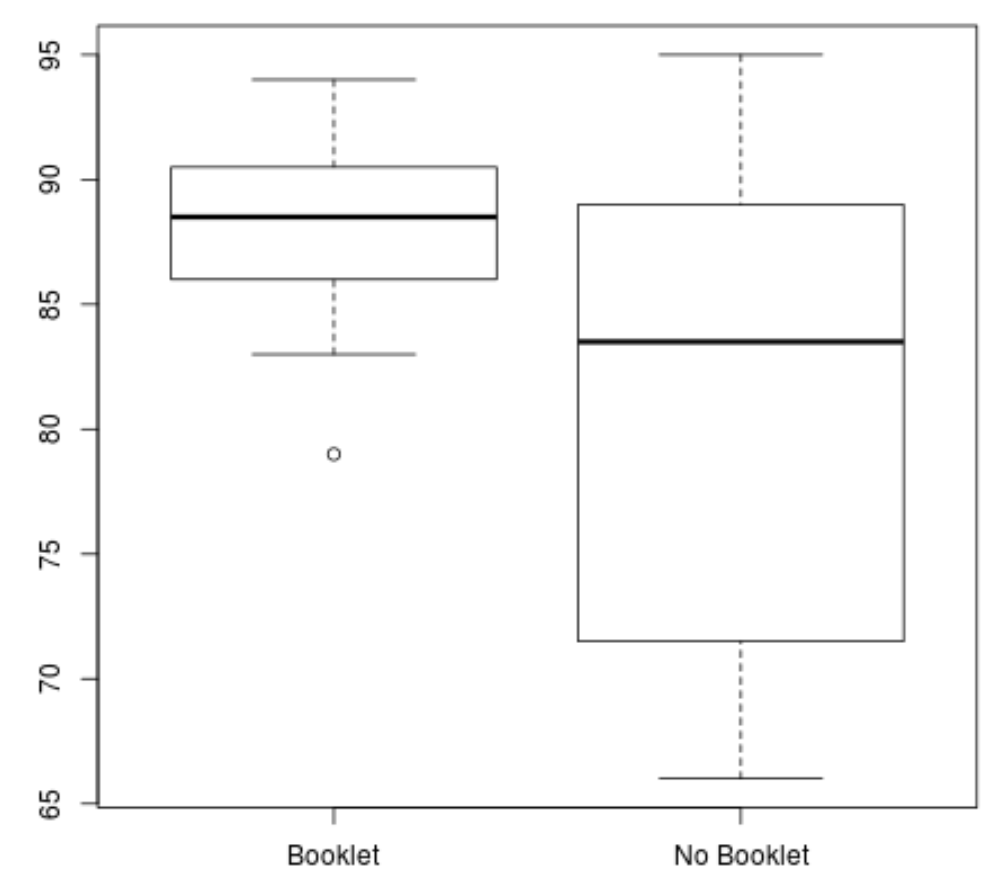
Мы можем ясно видеть, что группа «Буклет» имеет более высокий средний балл и более низкую дисперсию в баллах.
Чтобы формально проверить, существенно ли различаются средние баллы между группами, мы можем выполнить t-критерий Уэлча:
#perform Welch's t-test
t.test(booklet, no_booklet)
Welch Two Sample t-test
data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3048395 13.8618272
sample estimates:
mean of x mean of y
87.91667 80.83333
Из вывода мы видим, что тестовая статистика t равна 2,2361 , а соответствующее значение p равно 0,04171 .
Поскольку это p-значение меньше 0,05, мы можем отклонить нулевую гипотезу и заключить, что существует статистически значимая разница в средних результатах экзаменов между двумя группами.
Функция t.test() также предоставляет нам следующую информацию:
- 95% доверительный интервал для разницы в средних баллах по экзаменам между двумя группами составляет [0,3048, 13,8618 ].
- Средний экзаменационный балл первой группы – 87,91667 .
- Средний экзаменационный балл второй группы – 80,83333 .
Вы можете найти полную документацию по функции t.test() здесь .
Дополнительные ресурсы
Как выполнить t-тест для парных выборок в R
Как построить несколько блочных диаграмм на одной диаграмме в R