Когда мы хотим сравнить средства двух независимых групп, мы можем выбирать между использованием двух разных тестов:
Критерий Стьюдента: этот критерий предполагает, что обе группы данных взяты из совокупностей, которые следуют нормальному распределению и что обе совокупности имеют одинаковую дисперсию.
Критерий Уэлча: этот критерий предполагает, что обе группы данных взяты из совокупностей, которые следуют нормальному распределению, но не предполагает, что эти две совокупности имеют одинаковую дисперсию .
Разница между t-критерием Стьюдента и t-тестом Уэлча
Есть два различия в том, как выполняются t-критерий Стьюдента и t-критерий Уэлча:
- Тестовая статистика
- Степени свободы
t-критерий Стьюдента:
Статистика теста: ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 )
где x 1 и x 2 — средние значения выборки, n 1 и n 2 — объемы выборки для выборки 1 и выборки 2 соответственно, и где s p рассчитывается как:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
где s 1 2 и s 2 2 — выборочные дисперсии.
Степени свободы: n 1 + n 2 – 2
t-критерий Уэлча
Статистика теста: ( x 1 – x 2 ) / (√ s 1 2 / n 1 + s 2 2 / n 2 )
Степени свободы: (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / { [ (s 1 2 / n 1 ) 2 / (n 1 – 1) ] + [ (s 2 2 / n 2 ) 2 / (п 2 – 1) ] }
Формула для расчета степеней свободы для t-критерия Уэлча учитывает разницу между двумя стандартными отклонениями. Однако если две выборки имеют одинаковые стандартные отклонения, то степени свободы для t-критерия Уэлча будут такими же, как и степени свободы для t-критерия Стьюдента.
Как правило, стандартные отклонения для двух выборок неодинаковы, и, таким образом, степени свободы для t-критерия Уэлча, как правило, меньше, чем степени свободы для t-критерия Стьюдента.
Также важно отметить, что степени свободы для t-критерия Уэлча обычно не являются целыми числами. Если вы проводите тест вручную, лучше округлить до следующего наименьшего целого числа. Если вы используете статистическое программное обеспечение, такое как R , программное обеспечение сможет передать десятичное значение для степеней свободы.
Когда следует использовать t-критерий Уэлча?
Некоторые люди утверждают, что t-критерий Уэлча должен быть выбором по умолчанию для сравнения средних значений двух независимых групп, поскольку он работает лучше, чем t-критерий Стьюдента, когда размеры выборки и дисперсии между группами не равны, и дает идентичные результаты, когда размеры выборки дисперсии равны.
На практике, когда вы сравниваете средние значения двух групп, маловероятно, что стандартные отклонения для каждой группы будут одинаковыми. Это делает хорошей идеей просто всегда использовать t-критерий Уэлча, чтобы вам не приходилось делать никаких предположений о равных дисперсиях.
Примеры использования t-критерия Уэлча
Затем мы выполним t-критерий Уэлча для следующих двух выборок, чтобы определить, значительно ли различаются средние значения их популяций при уровне значимости 0,05:
Образец 1: 14, 15, 15, 15, 16, 18, 22, 23, 24, 25, 25
Образец 2: 10, 12, 14, 15, 18, 22, 24, 27, 31, 33, 34, 34, 34
Мы проиллюстрируем, как проводить тест тремя различными способами:
- Рукой
- Использование MicrosoftExcel
- Использование статистического языка программирования R
Т-критерий Уэлча от руки
Чтобы провести t-критерий Уэлча вручную, нам сначала нужно найти выборочные средние, выборочные дисперсии и размеры выборки:
х 1 – 19,27
х 2 – 23,69
с 1 2 – 20,42
с 2 2 – 83,23
№ 1 – 11 № 2 – 13
Затем мы можем подставить эти числа, чтобы найти тестовую статистику:
Статистика теста: ( x 1 – x 2 ) / (√ s 1 2 / n 1 + s 2 2 / n 2 )
Статистика теста: (19,27 – 23,69) / (√ 20,42/11 + 83,23/13 ) = -4,42 / 2,873 = -1,538
Степени свободы: (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / { [ (s 1 2 / n 1 ) 2 / (n 1 – 1) ] + [ (s 2 2 / n 2 ) 2 / (п 2 – 1) ] }
Степени свободы: (20,42/11 + 83,23/13) 2 / { [ (20,42/11) 2 / (11 – 1) ] + [ (83,23/13) 2 / (13 – 1) ] } = 18,137. Мы округляем это число до ближайшего ближайшего целого числа 18 .
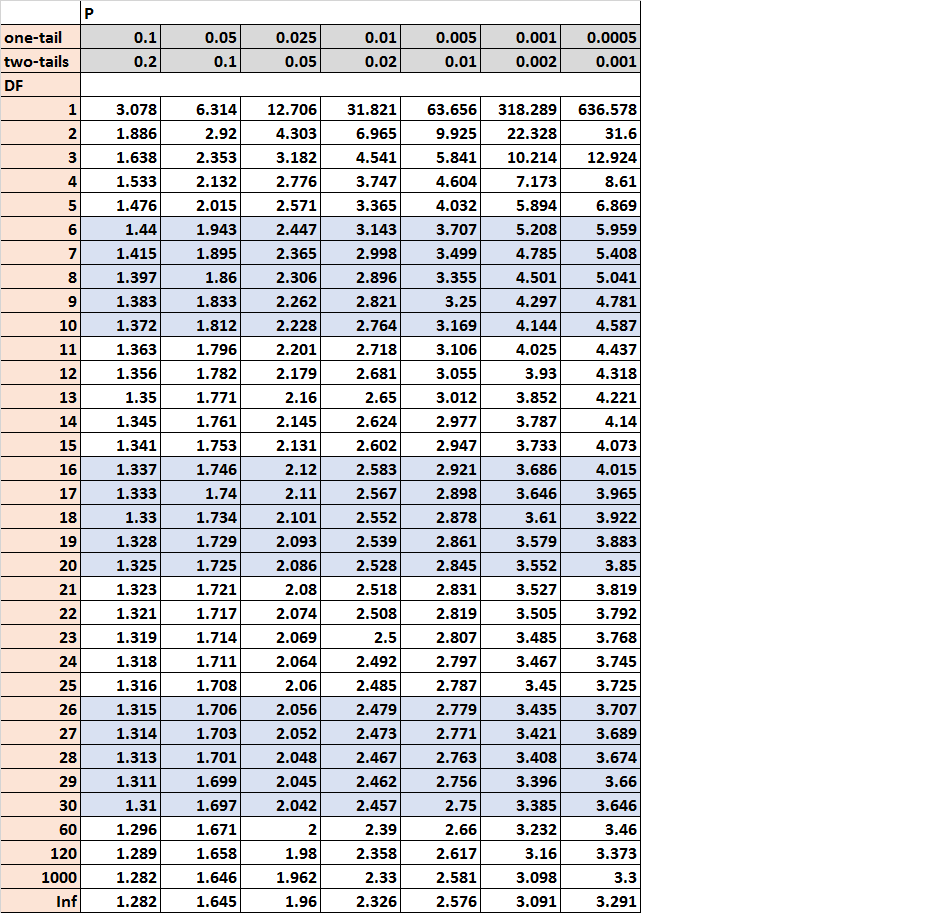
Наконец, мы найдем критическое значение t в таблице t-распределения, которое соответствует двустороннему критерию с альфа = 0,05 для 18 степеней свободы:
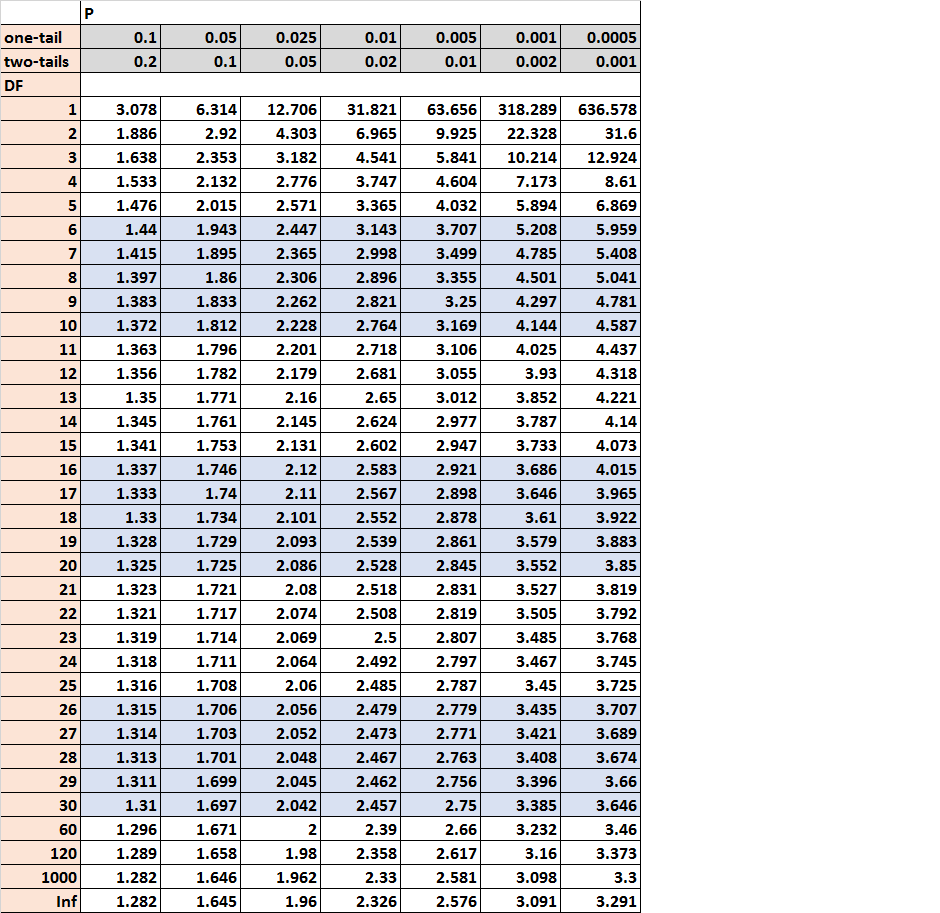
Критическое значение t равно 2,101.Поскольку абсолютное значение нашей тестовой статистики (1,538) не превышает критического значения t, мы не можем отвергнуть нулевую гипотезу теста. Нет достаточных доказательств, чтобы сказать, что средства двух популяций значительно различаются.
t-критерий Уэлча с использованием Excel
Чтобы провести t-критерий Уэлча в Excel, нам сначала нужно загрузить бесплатный пакет инструментов для анализа. Если вы еще не загрузили это в Excel, я написал краткое руководство о том, как его загрузить .
После того, как вы загрузили пакет инструментов для анализа, вы можете выполнить следующие шаги, чтобы провести t-критерий Уэлча для наших двух образцов:
1. Введите данные. Введите значения данных для двух образцов в столбцах A и B вместе с заголовками Sample 1 и Sample 2 в первой ячейке каждого столбца.

2. Проведите t-критерий Уэлча с помощью Analysis ToolPak. Перейдите на вкладку « Данные » на верхней ленте. Затем в группе « Анализ » щелкните значок пакета инструментов «Анализ».

В появившемся окне нажмите t-Test: Two Sample Assisting Unequal Variances , затем нажмите OK.

Наконец, заполните значения ниже и нажмите OK:

Должен появиться следующий вывод:

Обратите внимание, что результаты этого теста совпадают с результатами, которые мы получили вручную:
- Статистика теста -1,5379 .
- Критическое двустороннее значение равно 2,1009 .
- Поскольку абсолютное значение тестовой статистики не превышает критического двустороннего значения, средние значения двух популяций статистически не различаются.
- Кроме того, двустороннее p-значение теста составляет 0,14, что больше, чем 0,05, и подтверждает, что два средних значения совокупности статистически не различаются.
t-критерий Уэлча с использованием R
Следующий код иллюстрирует, как выполнить t-критерий Уэлча для наших двух выборок, используя язык статистического программирования R :
#create two vectors to hold sample data values
sample1 <- c(14, 15, 15, 15, 16, 18, 22, 23, 24, 25, 25)
sample2 <- c(10, 12, 14, 15, 18, 22, 24, 27, 31, 33, 34, 34, 34)
#conduct Welch's test
t.test( sample1, sample2)
# Welch Two Sample t-test
#
#data: sample1 and sample2
#t = -1.5379, df = 18.137, p-value = 0.1413
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -10.453875 1.614714
#sample estimates:
#mean of x mean of y
# 19.27273 23.69231
#
Функция t.test() отображает следующий соответствующий вывод:
- t: тестовая статистика = -1,5379
- df : степени свободы = 18,137
- p-значение: p-значение двустороннего теста = 0,1413
- 95% доверительный интервал : 95%доверительный интервал для истинной разницы в средних значениях населения = (-10,45, 1,61)
Результаты этого теста совпадают с результатами, полученными вручную и с помощью Excel: разница в средних значениях для этих двух популяций не является статистически значимой на уровне альфа = 0,05.