Всякий раз, когда вы проводите проверку гипотезы, в результате вы получаете тестовую статистику. Чтобы определить, являются ли результаты проверки гипотезы статистически значимыми, можно сравнить статистику проверки с критическим значением Z. Если абсолютное значение тестовой статистики больше критического значения Z, то результаты теста статистически значимы.
Чтобы найти критическое значение Z на калькуляторе TI-84, мы можем использовать следующую функцию:
invNorm(вероятность, μ, σ)
куда:
- вероятность: уровень значимости
- μ: среднее значение населения
- σ: стандартное отклонение населения
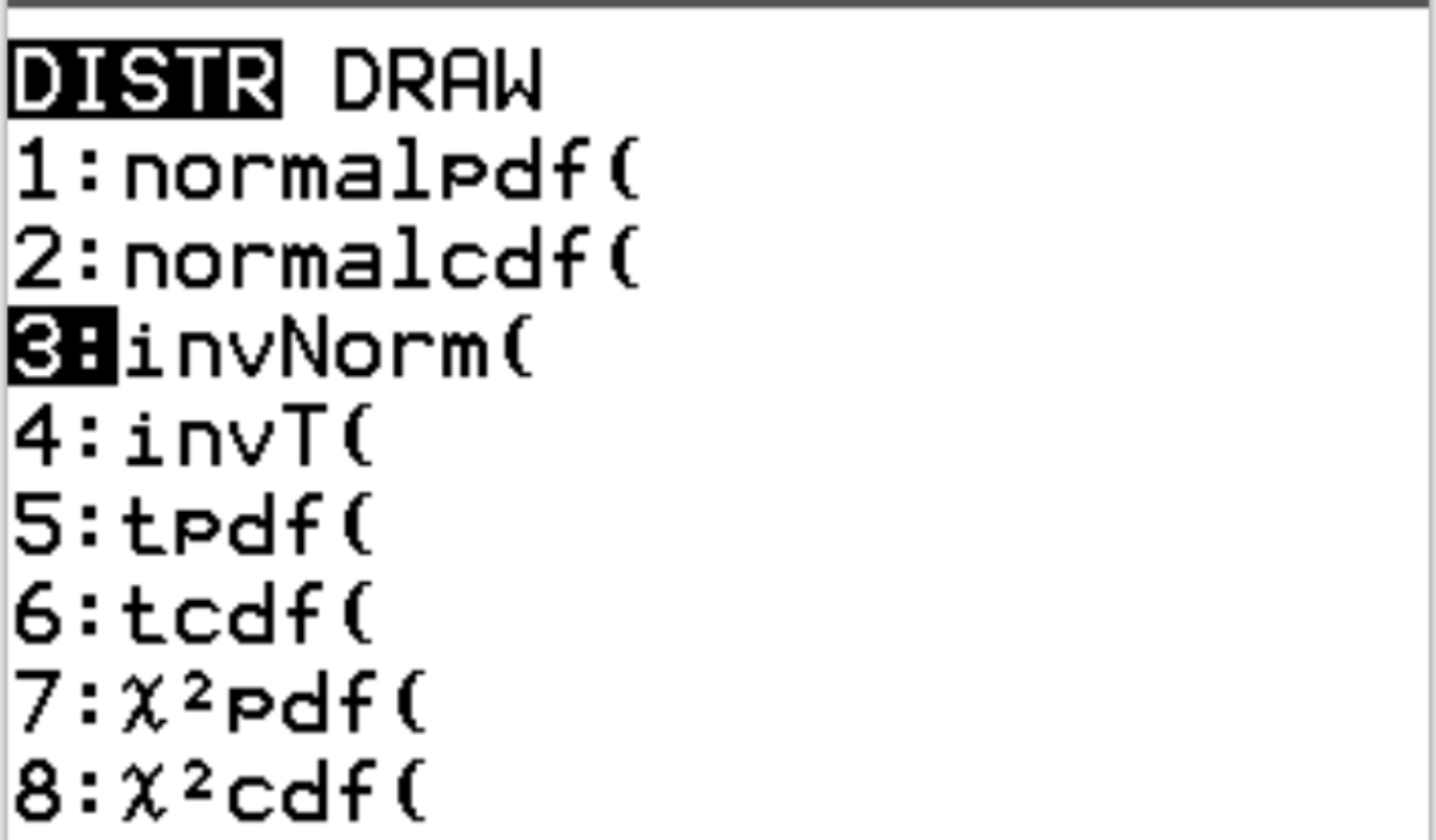
Вы можете получить доступ к этой функции на калькуляторе TI-84, нажав 2nd , а затем нажав vars.Это приведет вас к экрану DISTR , где вы сможете использовать invNorm() :
В этом руководстве приведены несколько примеров использования функции invNorm() для поиска критических значений Z на калькуляторе TI-84.
Пример 1. Критическое значение Z для левостороннего теста
Вопрос: Найдите критическое значение Z для левостороннего критерия с уровнем значимости 0,05.
Ответ: invNorm(0,05, 0, 1) = -1,6449
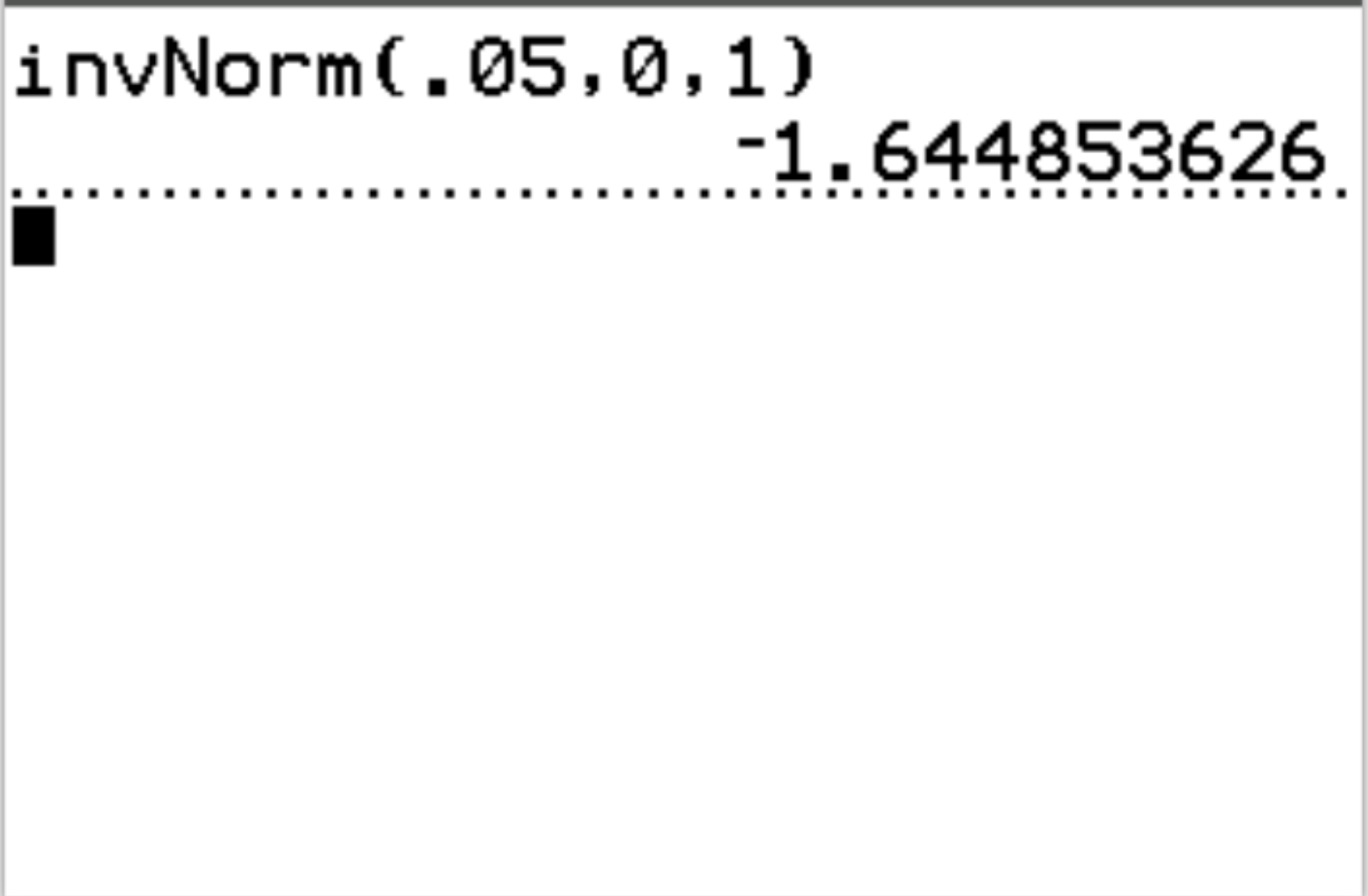
Интерпретация: Если тестовая статистика теста меньше -1,6449 , то результаты теста статистически значимы при α = 0,05.
Пример 2. Критическое значение Z для правостороннего теста
Вопрос: Найдите критическое значение Z для правостороннего критерия с уровнем значимости 0,10.
Ответ: invT(1-0,10, 0, 1) = 1,2816
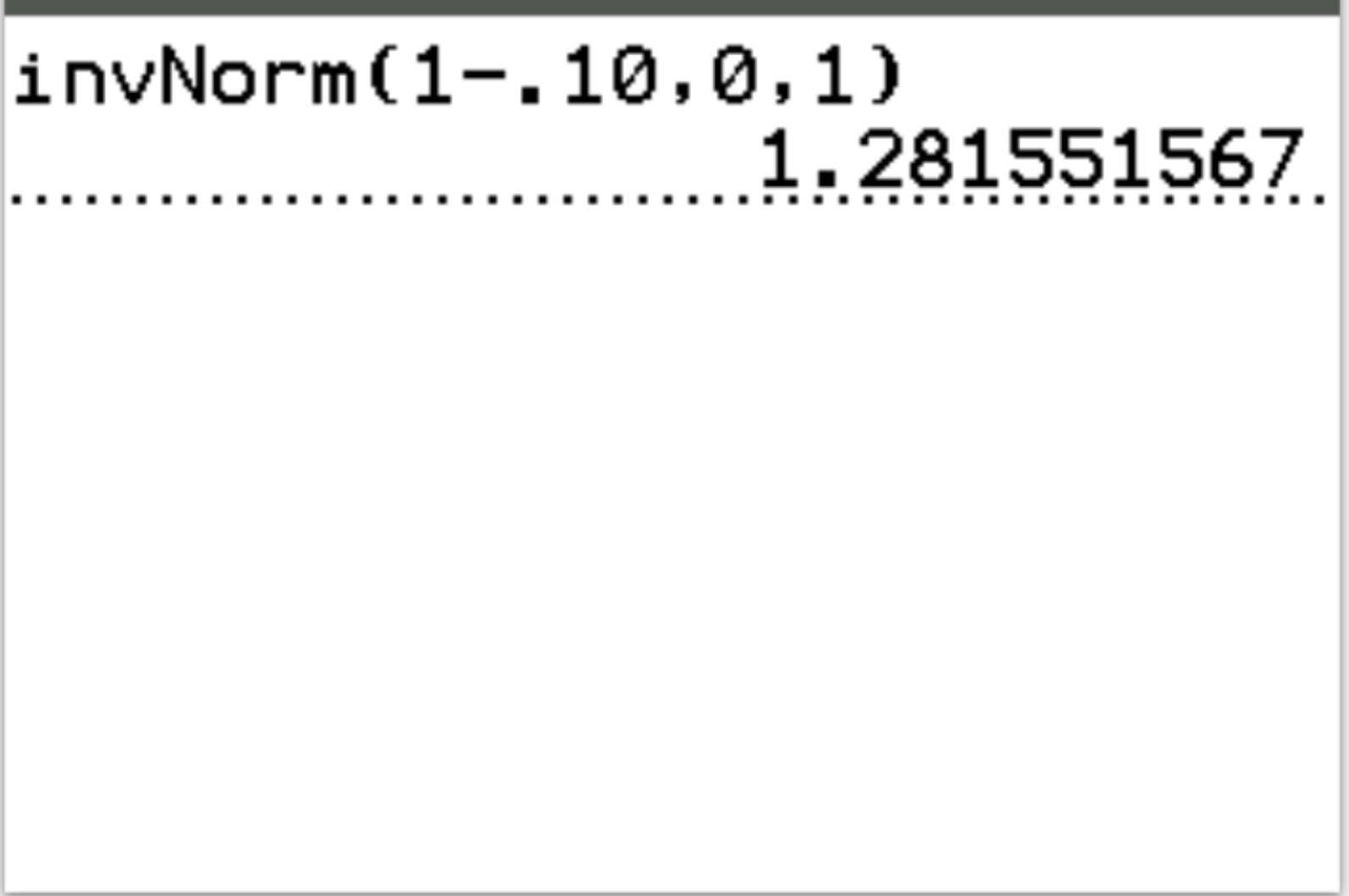
Интерпретация: Если критерий статистики теста больше 1,2816 , то результаты теста статистически значимы при α = 0,10.
Пример 3: Критическое значение Z для двустороннего теста
Вопрос: Найдите критическое значение Z для двустороннего критерия с уровнем значимости 0,05.
Ответ: invNorm(.05/2, 0, 1) = -1,96, 1,96
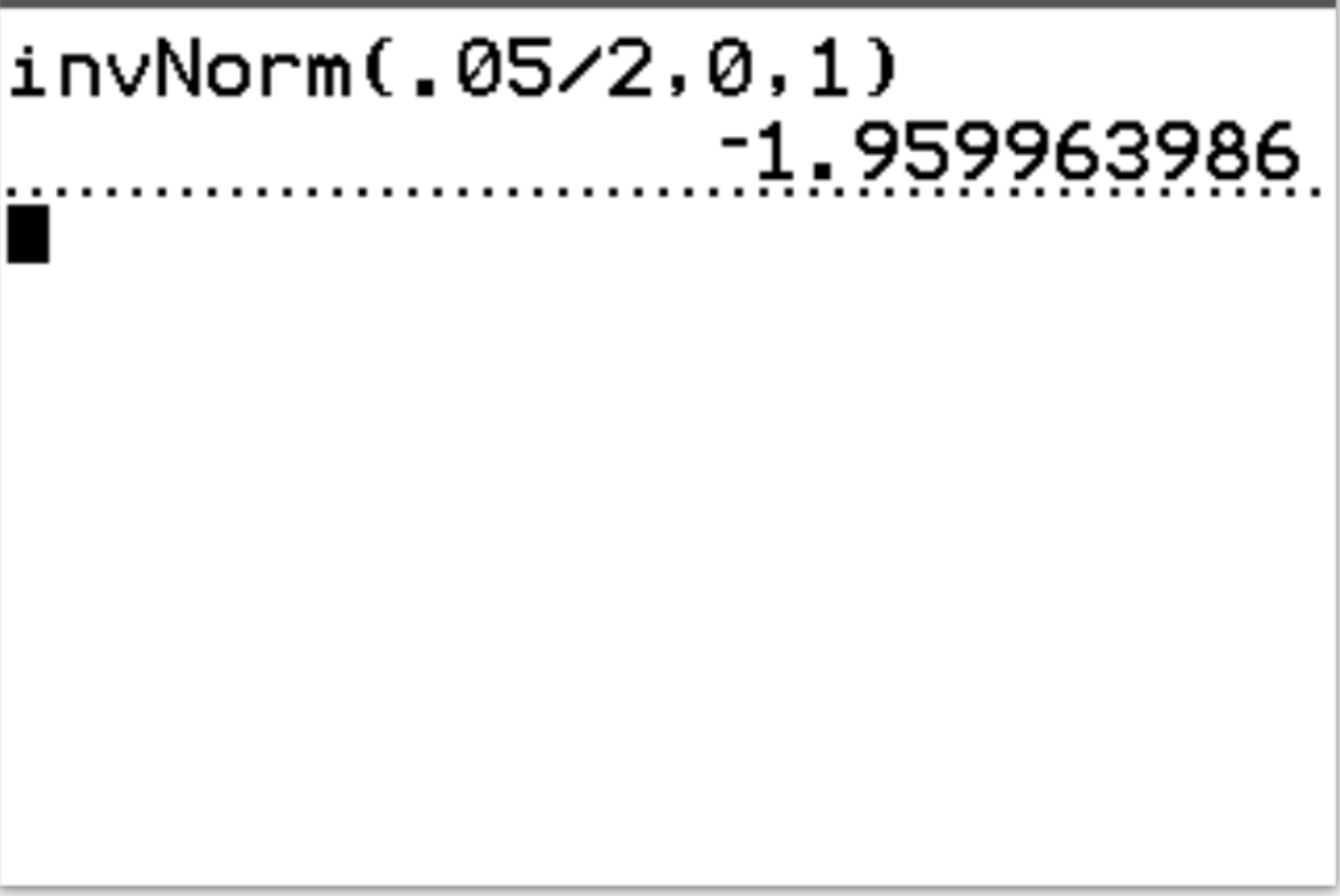
Интерпретация: поскольку это двусторонний тест, у нас фактически есть два критических значения: -1,96 и 1,96.Если тестовая статистика теста меньше -1,96 или больше 1,96 , то результаты теста статистически значимы при α = 0,05.