В статистике односторонний дисперсионный анализ используется для сравнения средних значений трех или более независимых групп, чтобы определить, существует ли статистически значимая разница между соответствующими средними значениями генеральной совокупности.
Одна метрика, которую мы всегда рассчитываем при использовании ANOVA, — это общее среднее , которое представляет собой среднее значение для всех наблюдений в наборе данных.
Он рассчитывается как:
Общее среднее = Σx i / n
куда:
- x i : i -е наблюдение в наборе данных
- n : общее количество наблюдений в наборе данных.
Большое среднее важно, потому что оно используется в формуле для вычисления общей суммы квадратов, что является важным значением, которое попадает в окончательную таблицу ANOVA.
В следующем примере показано, как на практике вычислить среднее значение для дисперсионного анализа.
Пример: расчет общего среднего в ANOVA
Предположим, мы хотим знать, приводят ли три разные программы подготовки к экзаменам к разным средним баллам на определенном экзамене. Чтобы проверить это, мы набираем 30 студентов для участия в исследовании и разделяем их на три группы.
Студенты в каждой группе случайным образом назначаются для использования одной из трех программ подготовки к экзамену в течение месяца для подготовки к экзамену. В конце месяца все студенты сдают один и тот же экзамен.
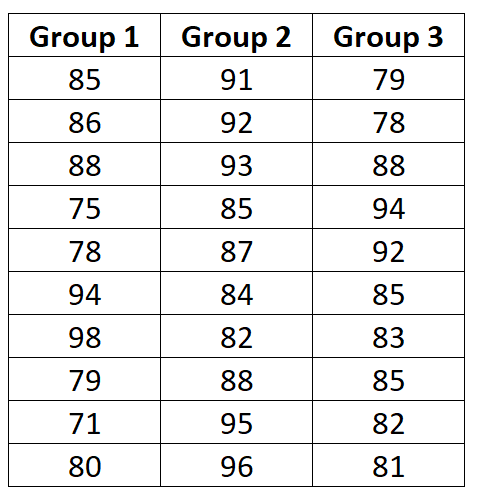
Ниже представлены результаты экзаменов для каждой группы:
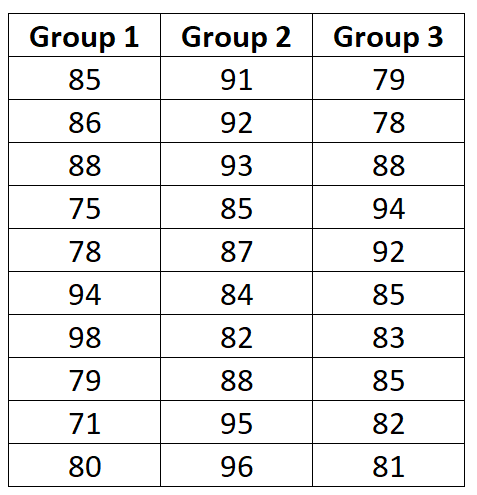
Чтобы вычислить среднее значение для этого набора данных, мы просто суммируем все наблюдения, а затем делим на общее количество наблюдений:
Общее среднее: (85 + 86 + 88 + 75 + 78 + 94 + 98 + 79 + 71 + 80 + 91 + 92 + 93 + 85 + 87 + 84 + 82 + 88 + 95 + 96 + 79 + 78 + 88 + 94 + 92 + 85 + 83 + 85 + 82 + 81) / 30 = 85,8 .
Среднее значение равно 85,8. Это средний балл за экзамен для всех 30 студентов.
Обратите внимание, что это значение не обязательно будет соответствовать среднему значению отдельной группы.
Например, если мы вычислим среднее значение для каждой группы студентов, мы обнаружим, что ни одно из средних значений группы на самом деле не соответствует общему среднему (или «общему» среднему):
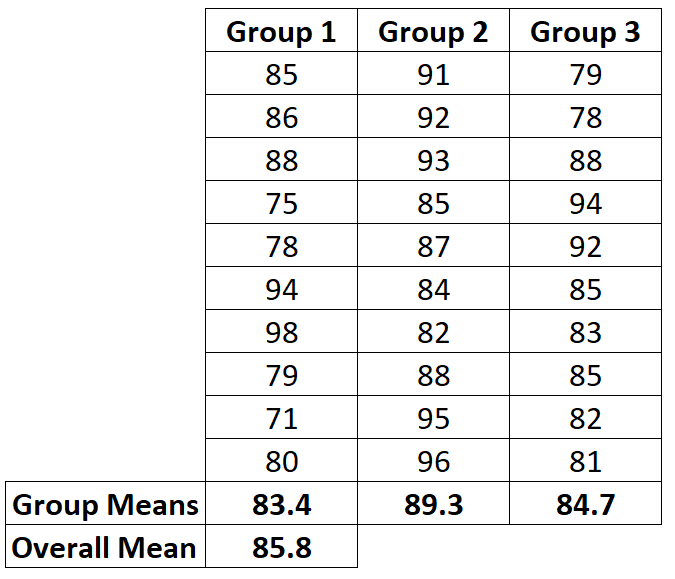
Это общее среднее затем используется в формуле для расчета общей суммы квадратов , которая рассчитывается как сумма квадратов отклонений между каждым отдельным наблюдением и общим средним:
Общая сумма квадратов: (85 – 85,8) 2 + (86 – 85,8) 2 + (88 – 85,8) 2 +...+ (82 – 85,8) 2 + (81 – 85,8) 2 = 1292,8 .
Затем это значение в конечном итоге используется в окончательной таблице ANOVA:
| Источник | Сумма квадратов (СС) | дф | Средние квадраты (MS) | Ф | | --- | --- | --- | --- | --- | | Уход | 192,2 | 2 | 96,1 | 2,358 | | Ошибка | 1100,6 | 27 | 40,8 | | | Общий | 1292,8 | 29 | | |
Связанный: Как интерпретировать F-значение и P-значение в ANOVA
Хорошей новостью является то, что вам редко придется вычислять среднее значение для дисперсионного анализа вручную, поскольку большинство статистических программ могут сделать это за вас.
Однако полезно знать, как рассчитывается общее среднее и как оно фактически используется в таблице ANOVA.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнить односторонний ANOVA на практике:
Как выполнить однофакторный дисперсионный анализ вручную
Как выполнить однофакторный дисперсионный анализ в Excel
Как выполнить односторонний ANOVA в R