Смещение Берксона — это тип смещения, который возникает в исследованиях, когда две переменные кажутся отрицательно коррелированными в выборочных данных, но на самом деле имеют положительную корреляцию в общей совокупности .
Например, предположим, что Том хочет изучить корреляцию между качеством гамбургеров и качеством молочных коктейлей в местных ресторанах.
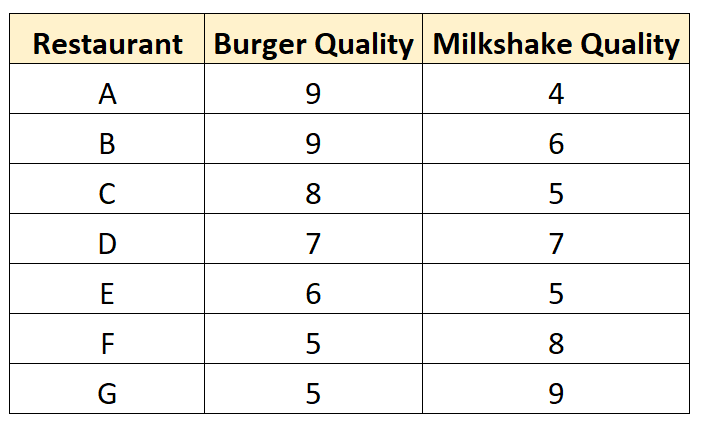
Он выходит и собирает следующие данные о семи разных ресторанах:
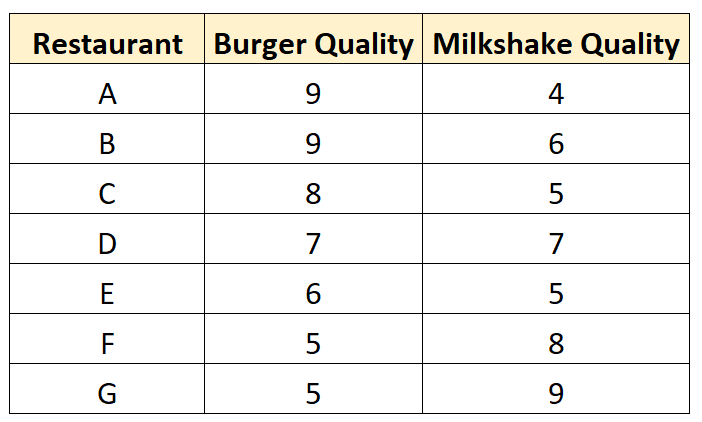
Он создает диаграмму рассеяния для визуализации данных:
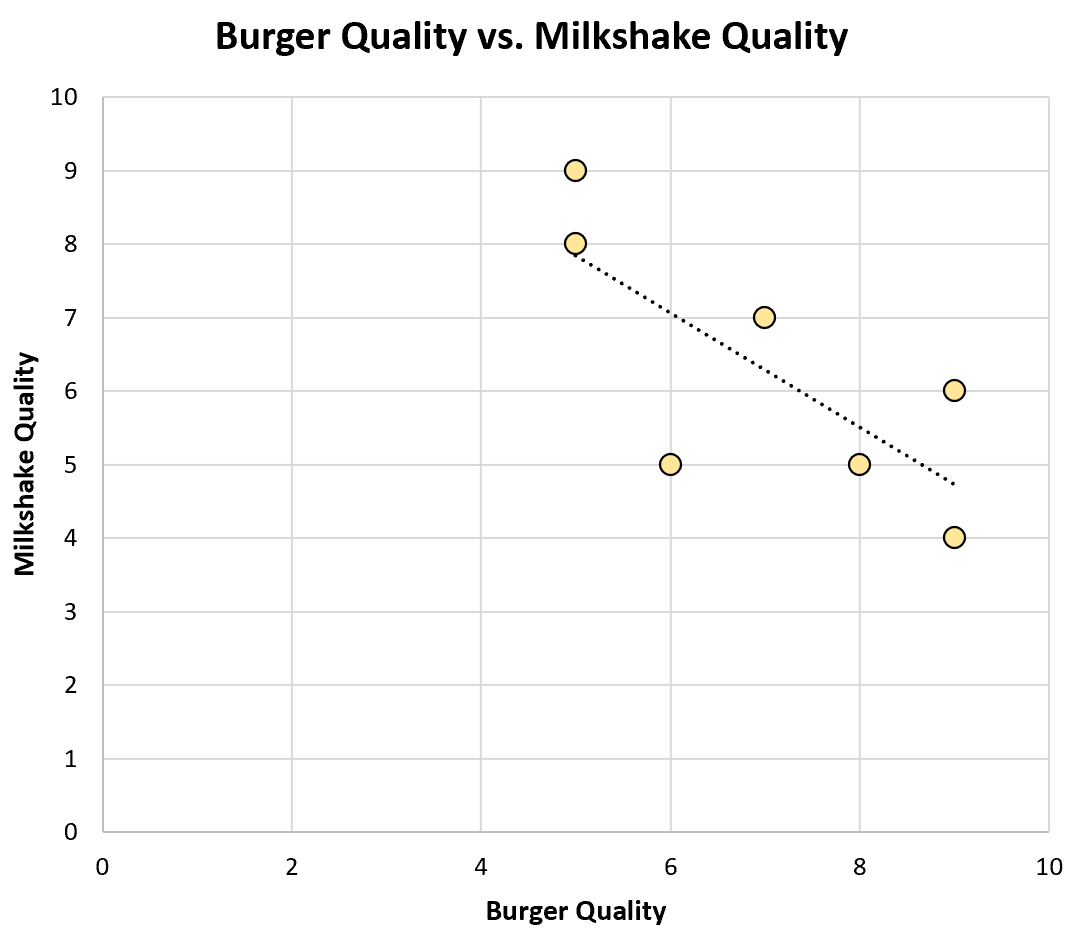
Коэффициенткорреляции Пирсона между этими двумя переменными составляет -0,75 , что является сильной отрицательной корреляцией.
Этот вывод противоречит здравому смыслу Тома — он думает, что в ресторанах, где готовят хорошие гамбургеры, также делают хорошие молочные коктейли.
Однако оказывается, что Том просто пропустил все рестораны в городе, которые делают и плохие гамбургеры, и плохие молочные коктейли.
Если бы он посетил эти рестораны, он бы собрал следующий набор данных:
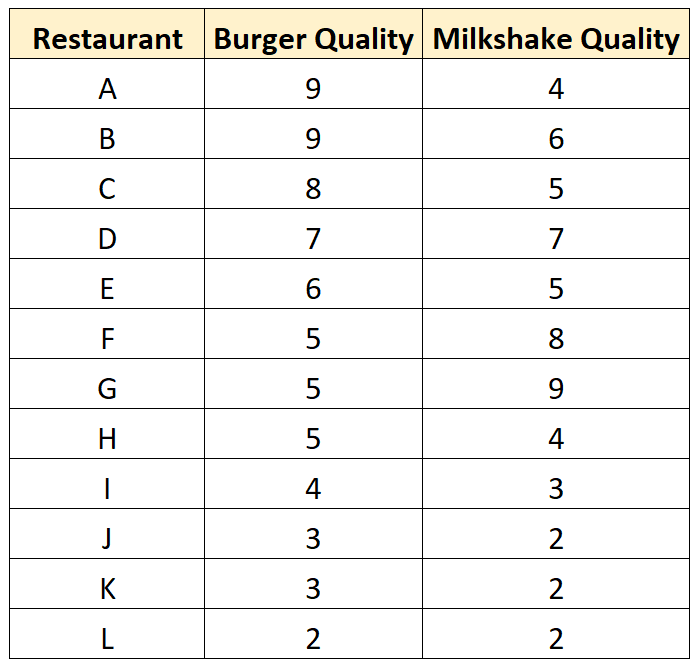
А вот как выглядит диаграмма рассеяния для этого набора данных:
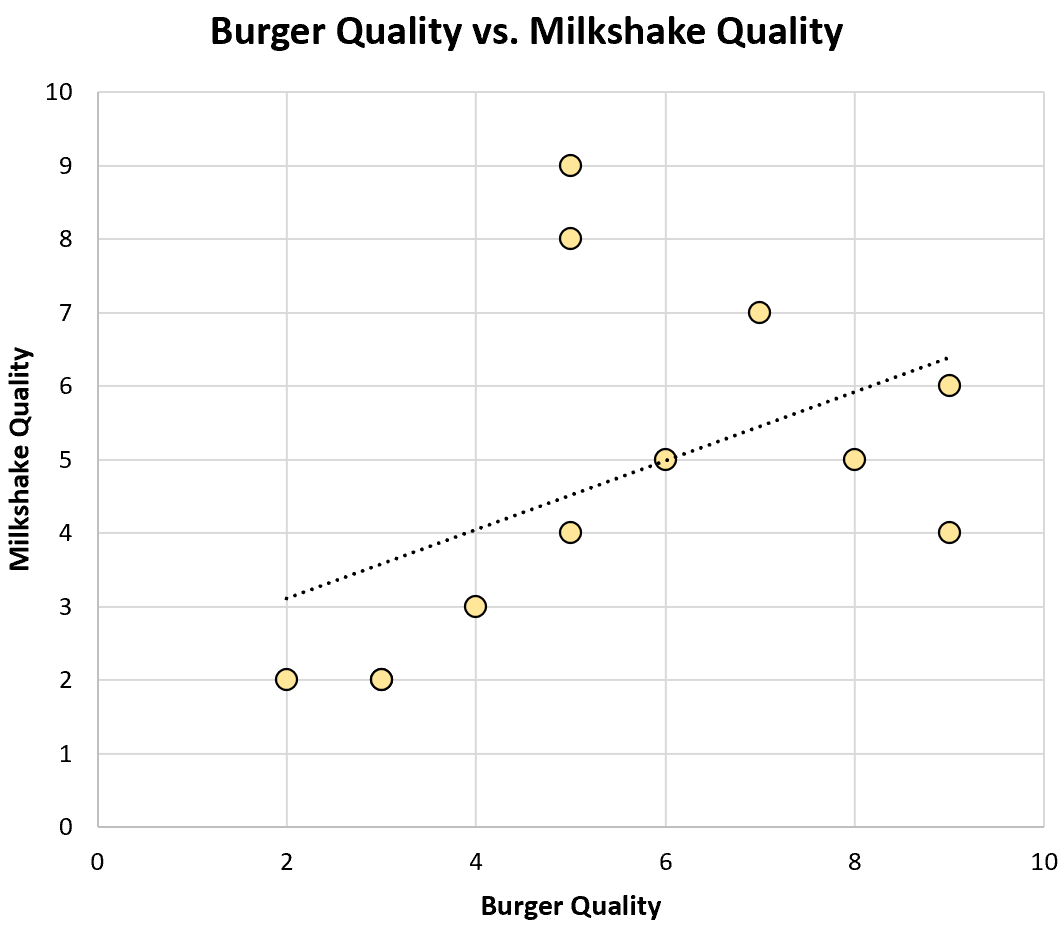
Коэффициенткорреляции Пирсона между двумя переменными оказывается равным 0,46 , что является умеренно сильной положительной корреляцией.
Изучив лишь часть ресторанов в городе, Том сделал ошибочный вывод об отрицательной корреляции между качеством бургеров и качеством молочных коктейлей.
В действительности между этими двумя переменными оказывается положительная связь (как и следовало ожидать). Это классический пример предвзятости Берксона.
Ознакомьтесь со следующими примерами, чтобы увидеть больше сценариев, в которых предвзятость Берксона проявляется на практике.
Пример 1: прием в колледж
Предположим, колледж принимает только студентов с достаточно высоким средним баллом и достаточно высоким баллом ACT.
Хорошо известно, что эти две переменные имеют положительную корреляцию, но оказывается, что среди студентов, решивших поступить в конкретный колледж, между ними наблюдается отрицательная корреляция.
Однако эта отрицательная корреляция возникает только потому, что студенты с высоким средним баллом и баллом ACT могут поступить в элитный университет, в то время как студенты с низким средним баллом и баллом ACT вообще не поступают.
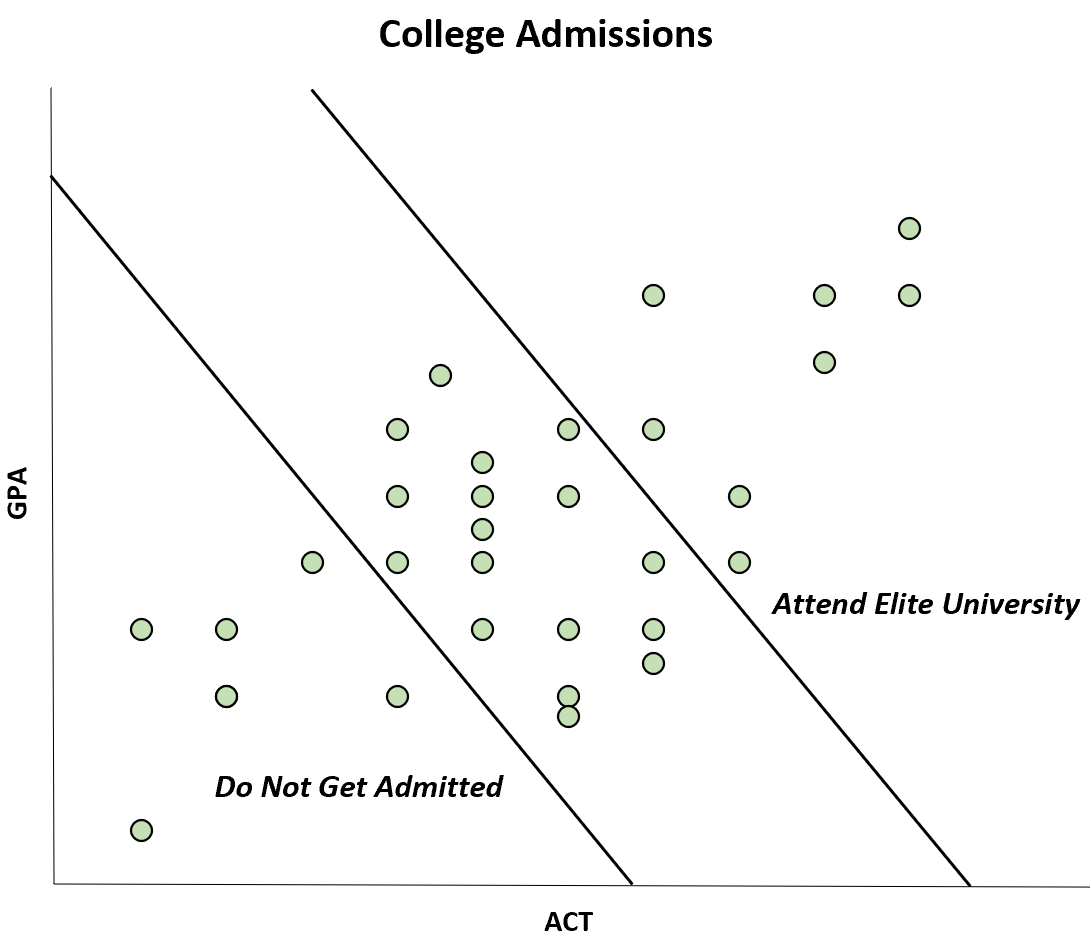
Хотя корреляция между ACT и GPA является положительной в популяции, в выборке корреляция оказывается отрицательной. Это случай предвзятости Берксона.
Пример 2: Предпочтения в отношении свиданий
Многие люди будут встречаться только с партнерами, которые одновременно привлекательны и имеют хороший характер.
В реальном мире может вообще не быть корреляции между этими двумя переменными, но при сужении круга знакомств человек может полностью игнорировать потенциальных партнеров, которые одновременно непривлекательны и обладают хорошим характером.
Таким образом, среди потенциальных партнеров может показаться, что существует отрицательная корреляция между этими двумя переменными: более привлекательные люди имеют худший характер, а люди с лучшим характером кажутся менее привлекательными.
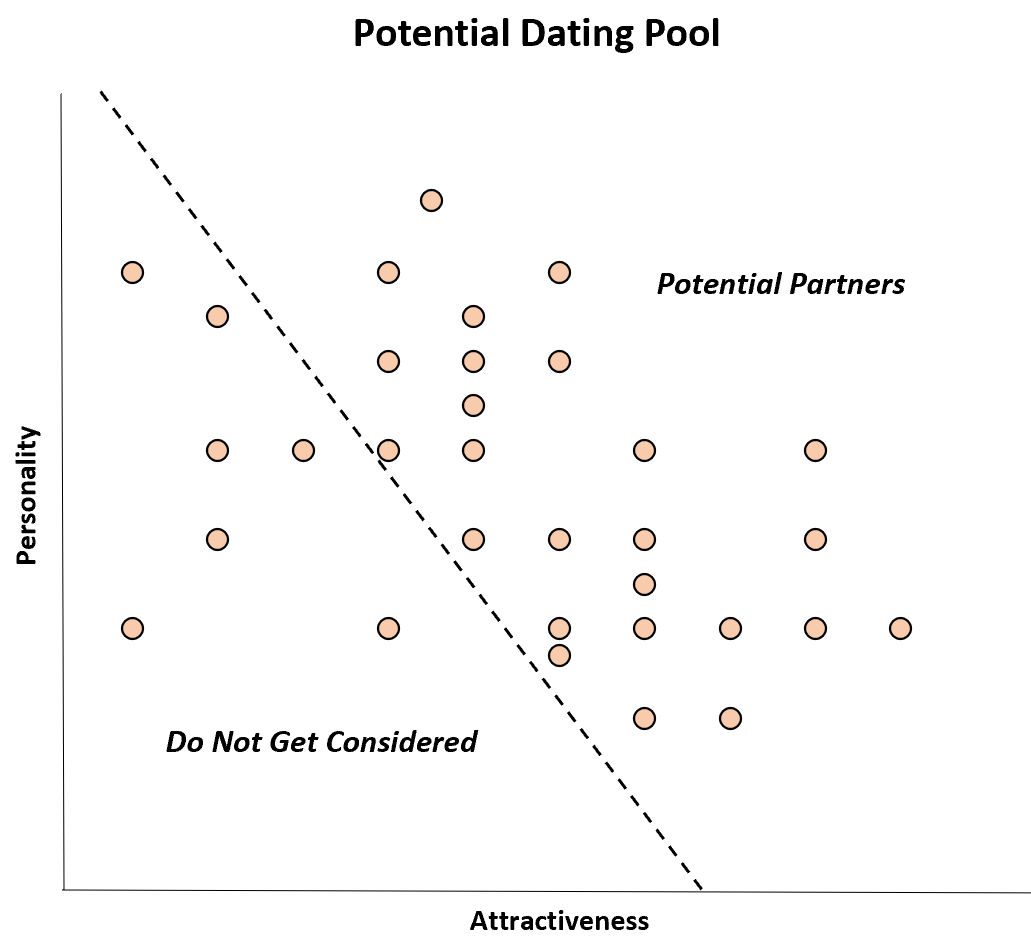
Хотя корреляции между этими двумя переменными в популяции нет, в выборке потенциальных партнеров корреляция, по-видимому, отрицательная. Это просто случай предвзятости Берксона.
Как предотвратить предвзятость Берксона
Самый очевидный способ предотвратить предвзятость Берксона в научных исследованиях — собрать простую случайную выборку из населения. То есть убедитесь, что каждый член интересующей совокупности имеет равные шансы быть включенным в выборку.
Например, если вы изучаете распространенность заболеваний в определенной стране, вам следует собрать выборку людей со всей страны, а не только тех, с кем удобно связаться в больницах.
Используя простую случайную выборку, исследователи могут максимизировать шансы того, что их выборка репрезентативна для населения , что означает, что они могут с уверенностью обобщать свои выводы из выборки на всю совокупность.