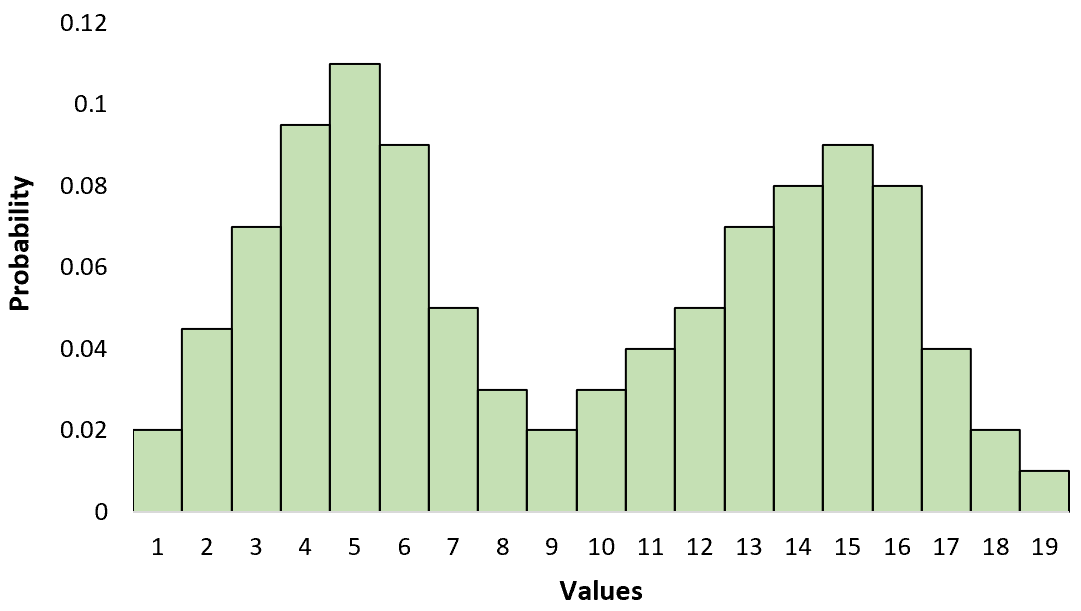
Бимодальное распределение — это распределение вероятностей с двумя модами.
Мы часто используем термин «мода» в описательной статистике для обозначения наиболее часто встречающегося значения в наборе данных, но в данном случае термин «мода» относится к локальному максимуму на диаграмме.
Когда вы визуализируете бимодальное распределение, вы заметите два отдельных «пика», которые представляют эти два режима.
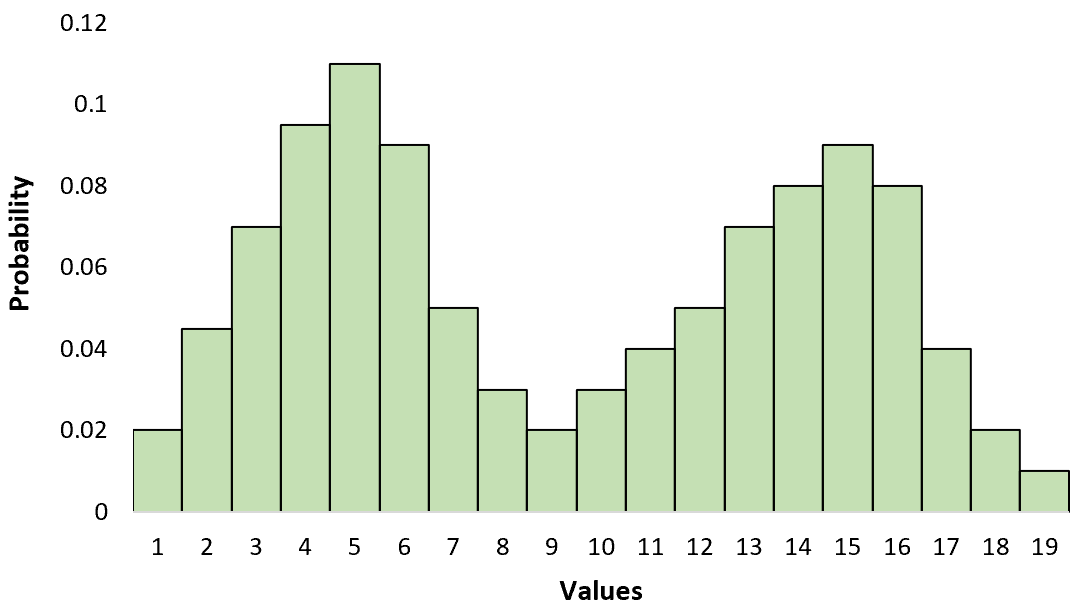
Это отличается от унимодального распределения, которое имеет только один пик:
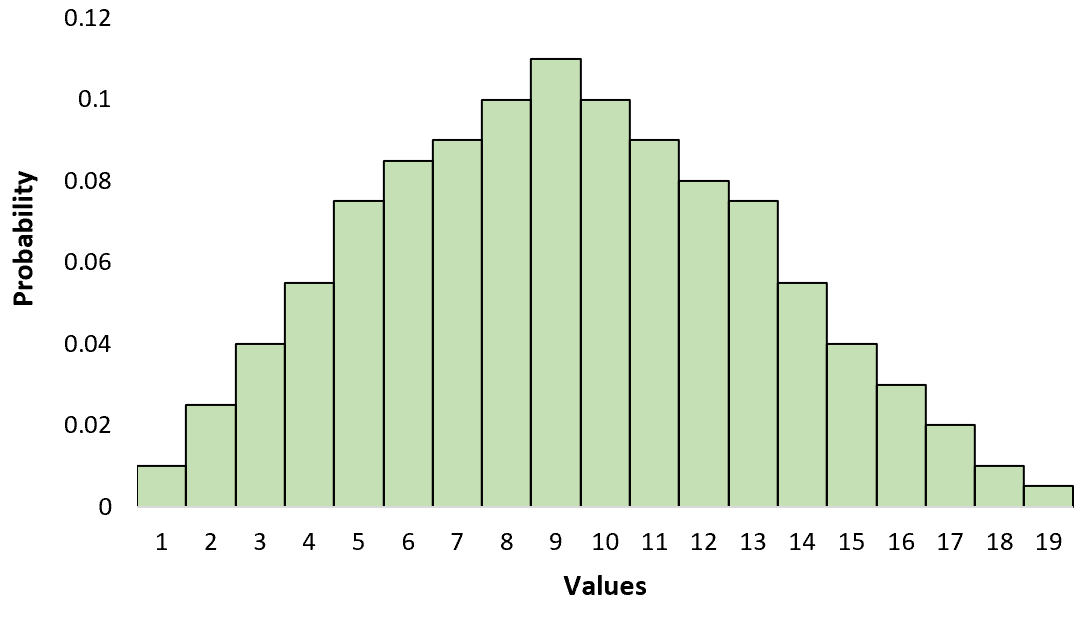
Вы можете запомнить разницу между ними, вспомнив:
- «би» = два
- «уни» = один
Хотя большинство курсов по статистике используют одномодальные распределения, такие как нормальное распределение , для объяснения различных тем, бимодальные распределения на самом деле довольно часто встречаются на практике, поэтому полезно знать, как их распознавать и интерпретировать.
Примечание. Бимодальное распределение — это особый тип мультимодального распределения .
Примеры бимодальных распределений
Вот несколько примеров бимодальных распределений:
Пример №1: часы пик в ресторане
Если вы создали график для визуализации распределения посетителей в определенном ресторане по часам, вы, вероятно, обнаружите, что он следует бимодальному распределению с пиком в обеденное время и еще одним пиком во время ужина:
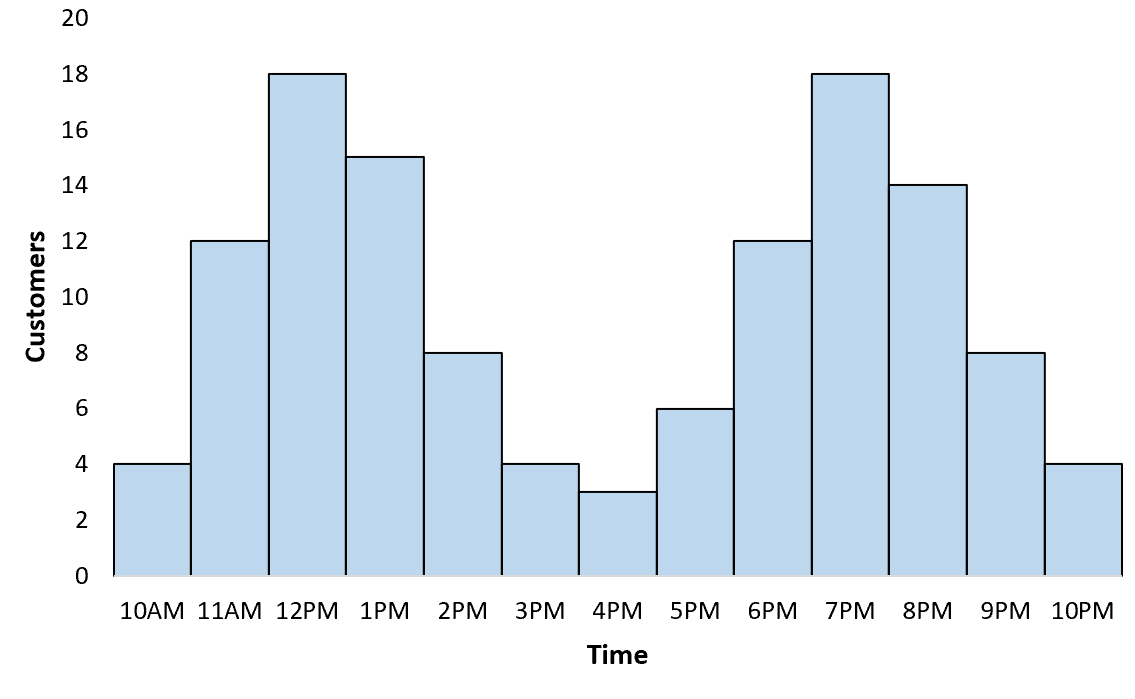
Пример №2: Средняя высота двух видов растений
Предположим, вы обошли поле и измерили высоту разных растений. Не осознавая этого, вы измеряете рост двух разных видов — одного довольно высокого, а другого довольно низкого. Если бы вы создали график для визуализации распределения высот, он бы следовал бимодальному распределению:
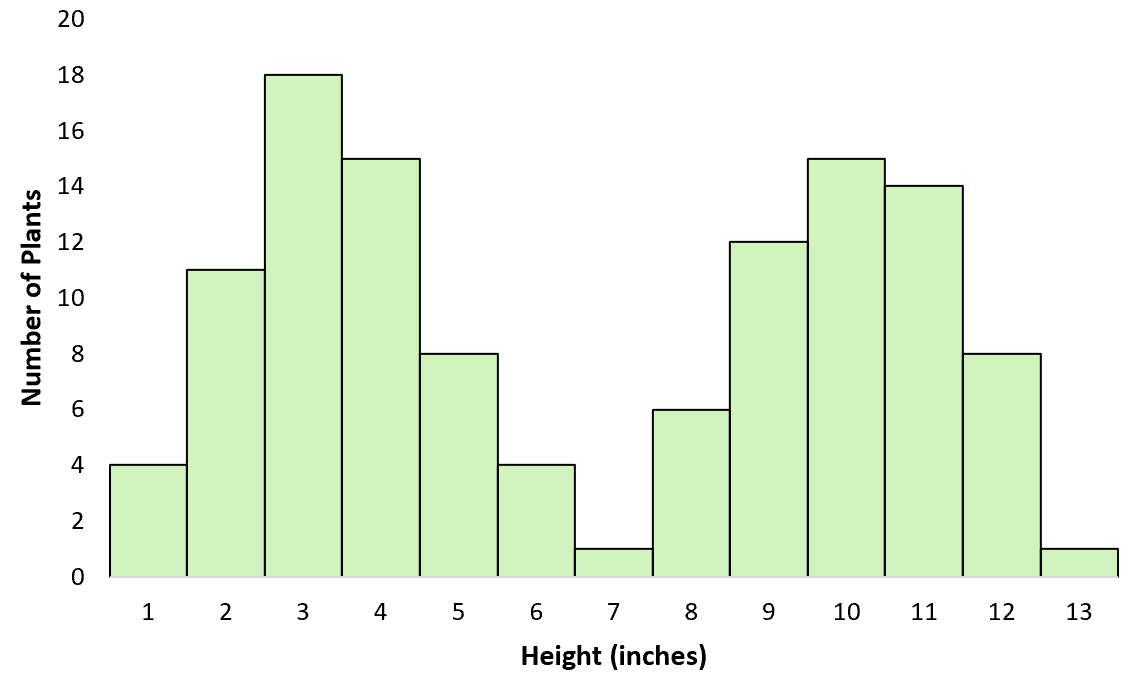
Пример №3: Экзаменационные баллы
Предположим, учитель сдает экзамен своим ученикам. Некоторые из студентов готовились к экзамену, а другие нет. Когда учитель создает график экзаменационных баллов, он следует бимодальному распределению с одним пиком вокруг низких баллов для студентов, которые не учились, и другим пиком для высоких баллов для студентов, которые учились:
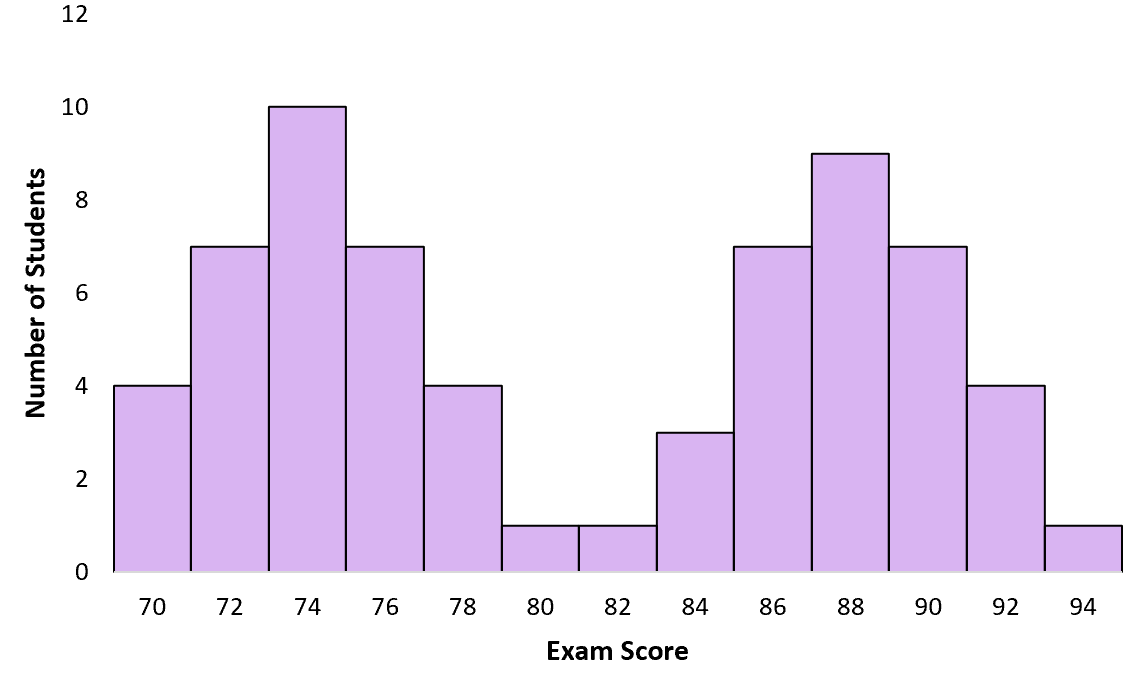
Что вызывает бимодальное распределение?
Обычно есть две вещи, которые вызывают бимодальное распределение:
1. Некоторые глубинные явления.
Часто бимодальные распределения возникают из-за некоторых лежащих в их основе явлений.
Например, количество клиентов, которые посещают ресторан каждый час, имеет бимодальное распределение, поскольку люди, как правило, едят вне дома в два разных времени: обед и ужин. Это лежащее в основе человеческого поведения является причиной бимодального распределения.
2. Объединение двух разных групп в одну кучу.
Бимодальные распределения также могут возникать, когда вы просто анализируете две разные группы вещей, не осознавая этого.
Например, если вы измеряете высоту растений на определенном поле, не осознавая, что на одном поле растут два разных вида, при создании диаграммы вы увидите бимодальное распределение.
Как анализировать бимодальные распределения
Мы часто описываем распределения, используя среднее значение или медиану , так как это дает нам представление о том, где находится «центр» распределения.
К сожалению, для бимодального распределения бесполезно знать среднее значение и медиану. Например, средний балл за экзамен для студентов в приведенном выше примере равен 81:
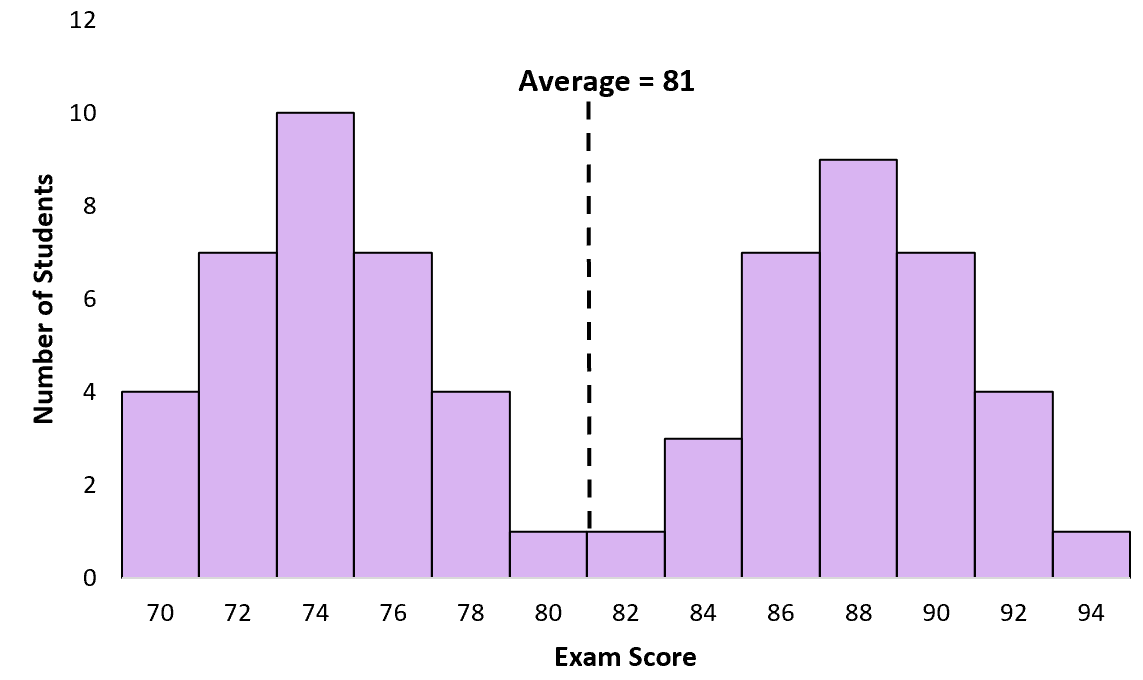
Однако очень немногие студенты на самом деле набрали близко к 81 баллу. В данном случае среднее значение вводит в заблуждение. Большинство студентов на самом деле набрали около 74 или около 88 баллов.
Лучший способ анализа и интерпретации бимодальных распределений — просто разбить данные на две отдельные группы, а затем проанализировать центр и распространение для каждой группы.
Например, мы можем разбить результаты экзамена на «низкие баллы» и «высокие баллы», а затем найти среднее значение и стандартное отклонение для каждой группы.
Если вы делитесь результатами какого-либо анализа, и ваши данные действительно следуют бимодальному распределению, полезно создать гистограмму, подобную показанной выше, чтобы ваша аудитория могла четко видеть, что распределение имеет два отдельных «пика» и что это только имеет смысл анализировать каждый пик отдельно, а не как один большой набор данных.