Хи-квадрат критерий согласия используется для определения того, следует ли категориальная переменная гипотетическому распределению.
В этом руководстве объясняется, как выполнить критерий согласия Хи-квадрат в Excel.
Пример: критерий согласия хи-квадрат в Excel
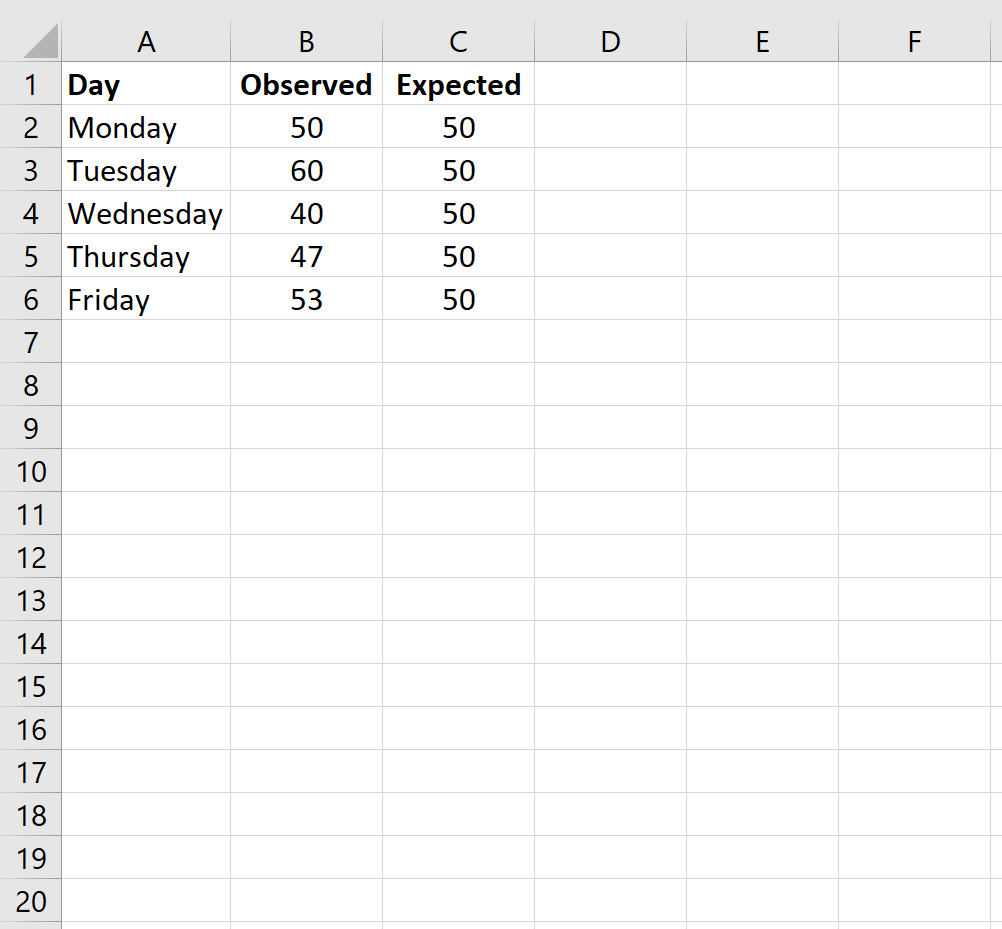
Владелец магазина утверждает, что каждый будний день в его магазин приходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, независимый исследователь записывает количество покупателей, которые заходят в магазин на определенной неделе, и обнаруживает следующее:
- Понедельник: 50 клиентов
- вторник: 60 клиентов
- Среда: 40 клиентов
- Четверг: 47 клиентов
- Пятница: 53 клиента
Мы будем использовать следующие шаги, чтобы выполнить критерий согласия Хи-квадрат, чтобы определить, согласуются ли данные с заявлением владельца магазина.
Шаг 1: Введите данные.
Во-первых, мы будем вводить значения данных для ожидаемого количества клиентов каждый день в одном столбце и наблюдаемое количество клиентов каждый день в другом столбце:
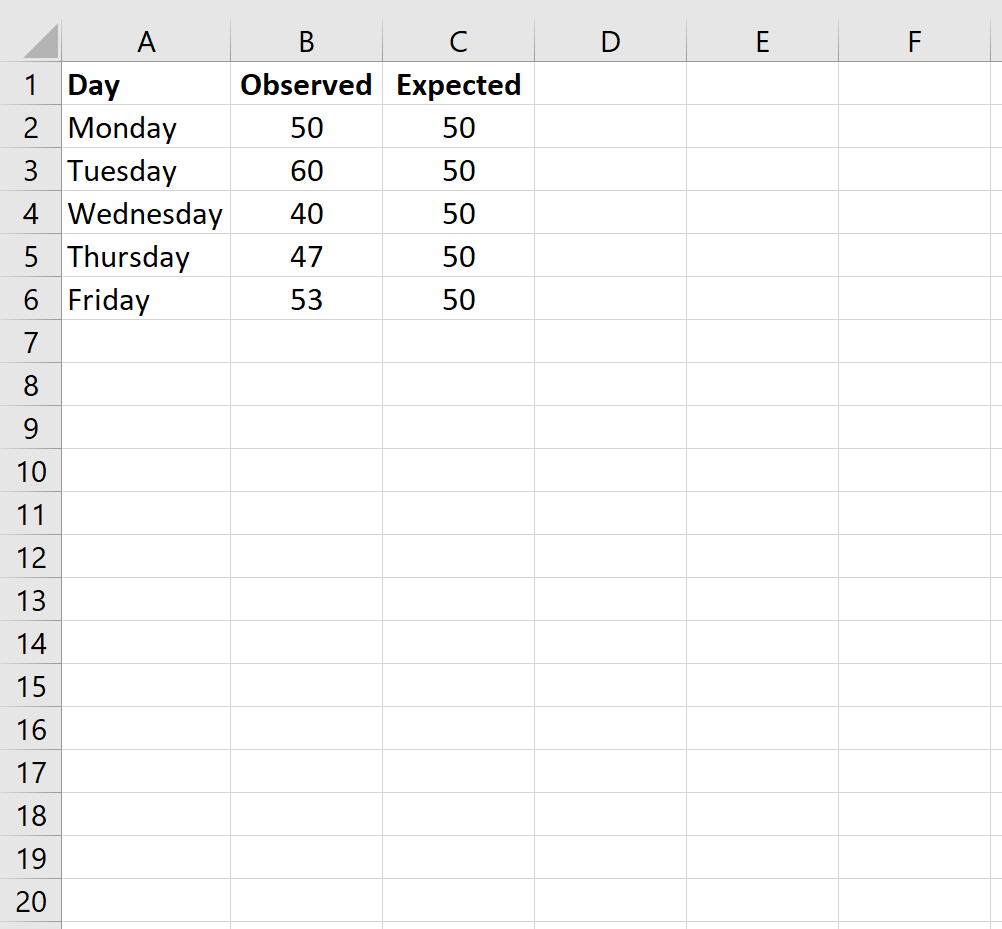
Примечание. Всего было 250 клиентов. Таким образом, если владелец магазина ожидает, что каждый день в магазин будет приходить такое же количество покупателей, то он ожидает 50 покупателей в день.
Шаг 2: Найдите разницу между наблюдаемыми и ожидаемыми значениями.
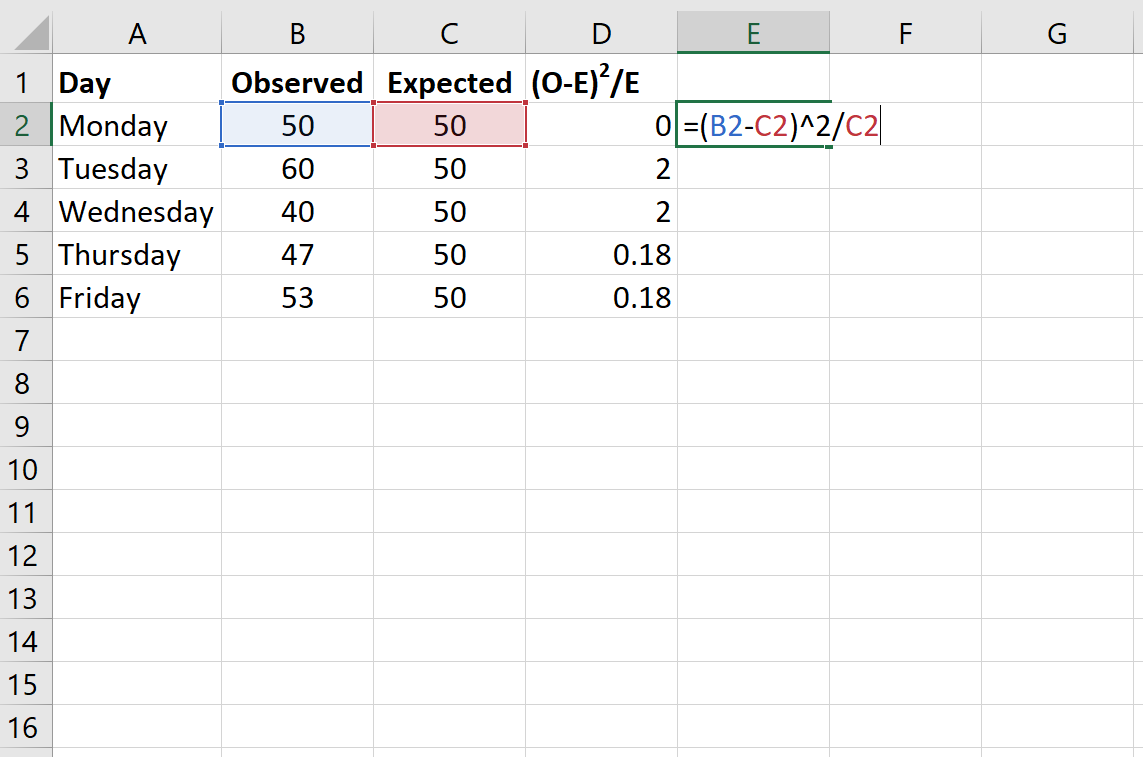
Статистика критерия хи-квадрат для теста согласия равна X 2 = Σ(OE) 2 / E
куда:
- Σ: причудливый символ, означающий «сумма».
- O: наблюдаемое значение
- E: ожидаемое значение
Следующая формула показывает, как рассчитать (OE) 2 / E для каждой строки:
Шаг 3: Рассчитайте статистику теста хи-квадрат и соответствующее значение p.
Наконец, мы рассчитаем статистику теста хи-квадрат вместе с соответствующим значением p, используя следующие формулы:
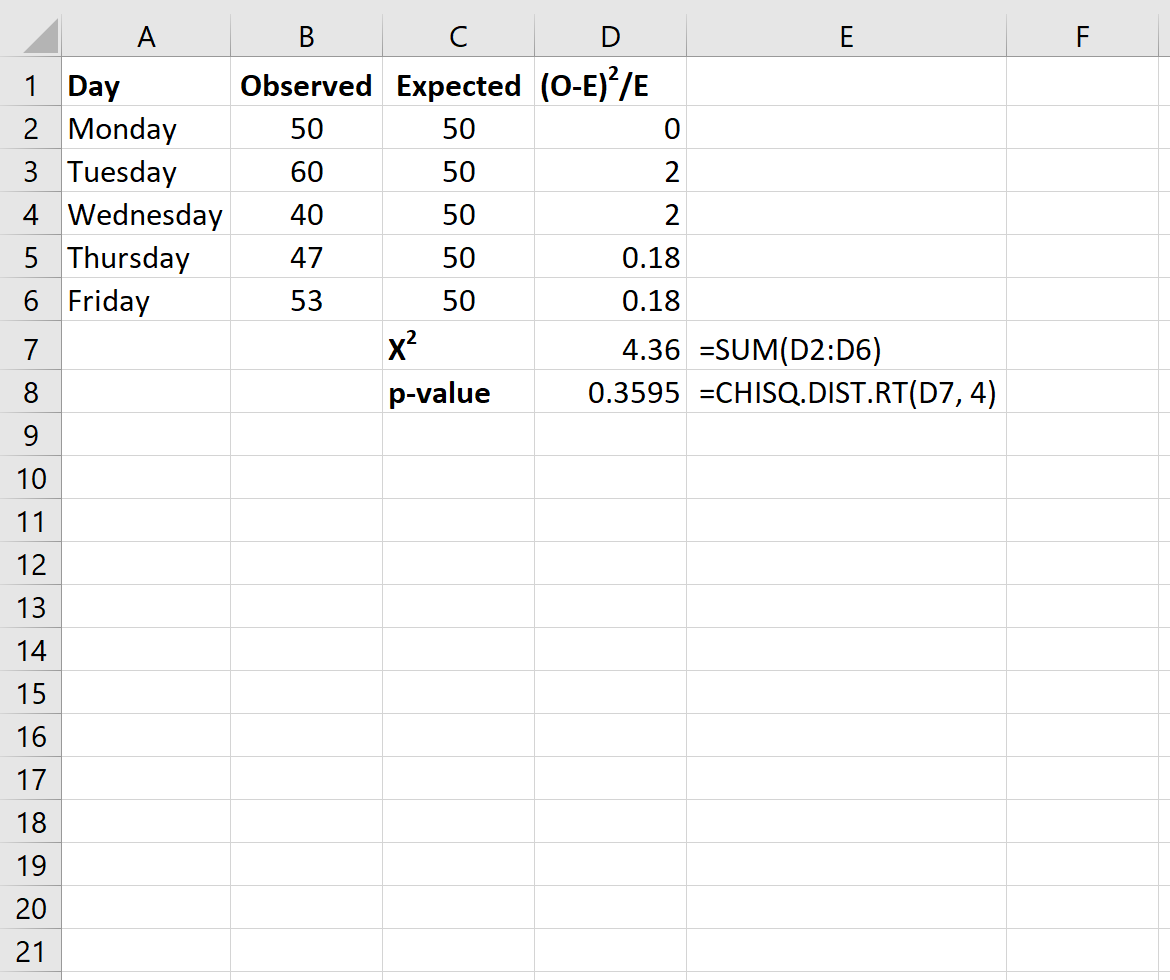
Примечание. Функция Excel ХИ.РАСП.ВР(x, степень_свободы) возвращает правостороннюю вероятность распределения хи-квадрат, связанную с тестовой статистикой x и определенными степенями свободы. Степени свободы рассчитываются как n-1. В этом случае deg_freedom = 5 – 1 = 4.
Шаг 4: Интерпретируйте результаты.
Статистика теста X 2 для теста составляет 4,36 , а соответствующее значение p равно 0,3595.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что истинное распределение покупателей отличается от распределения, о котором заявил владелец магазина.