Хи-квадрат критерий согласия используется для определения того, следует ли категориальная переменная гипотетическому распределению.
В этом руководстве объясняется, как выполнить критерий согласия Хи-квадрат в SPSS.
Пример: критерий согласия хи-квадрат в SPSS
Владелец магазина утверждает, что каждый будний день в его магазин приходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, исследователь записывает количество покупателей, которые заходят в магазин на определенной неделе, и обнаруживает следующее:
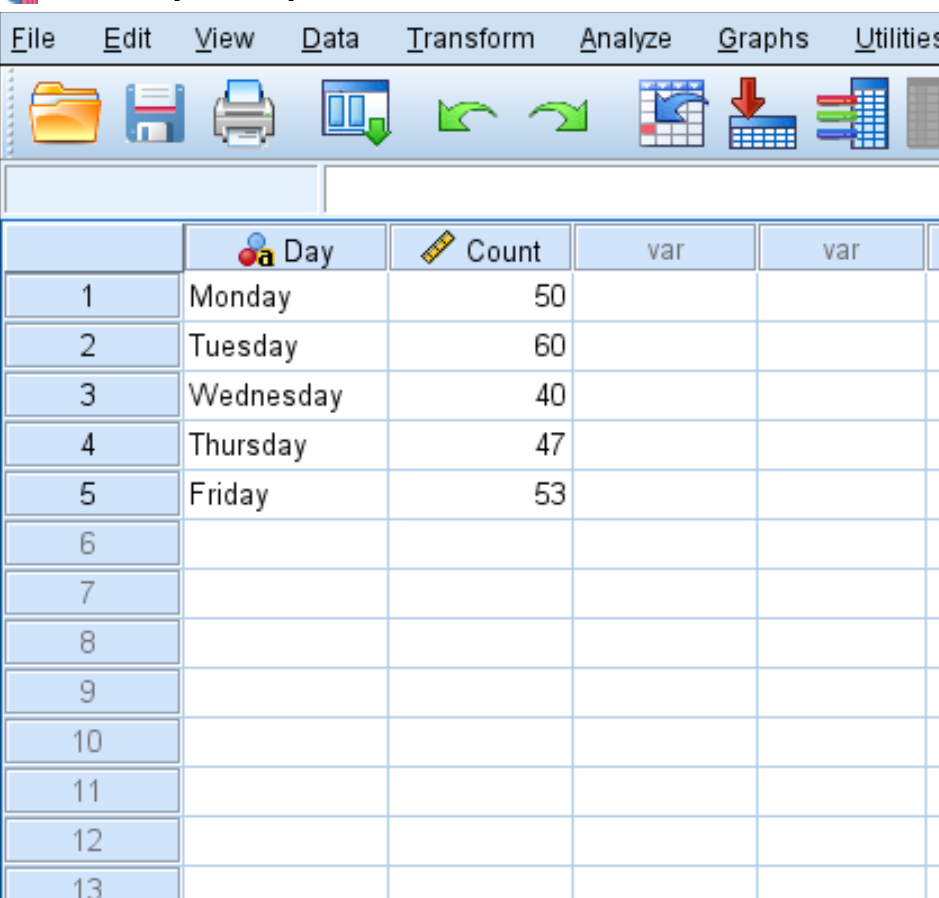
- Понедельник: 50 клиентов
- вторник: 60 клиентов
- Среда: 40 клиентов
- Четверг: 47 клиентов
- Пятница: 53 клиента
Выполните следующие действия, чтобы выполнить проверку соответствия Хи-квадрат в SPSS, чтобы определить, согласуются ли данные с заявлением владельца магазина.
Шаг 1: Введите данные.
Сначала введите данные в SPSS в следующем формате:
Шаг 2: Используйте взвешенные случаи.
Чтобы тест работал корректно, нам нужно указать SPSS, что переменная «День» должна быть взвешена переменной «Количество».
Перейдите на вкладку « Данные », затем « Весовые случаи »:
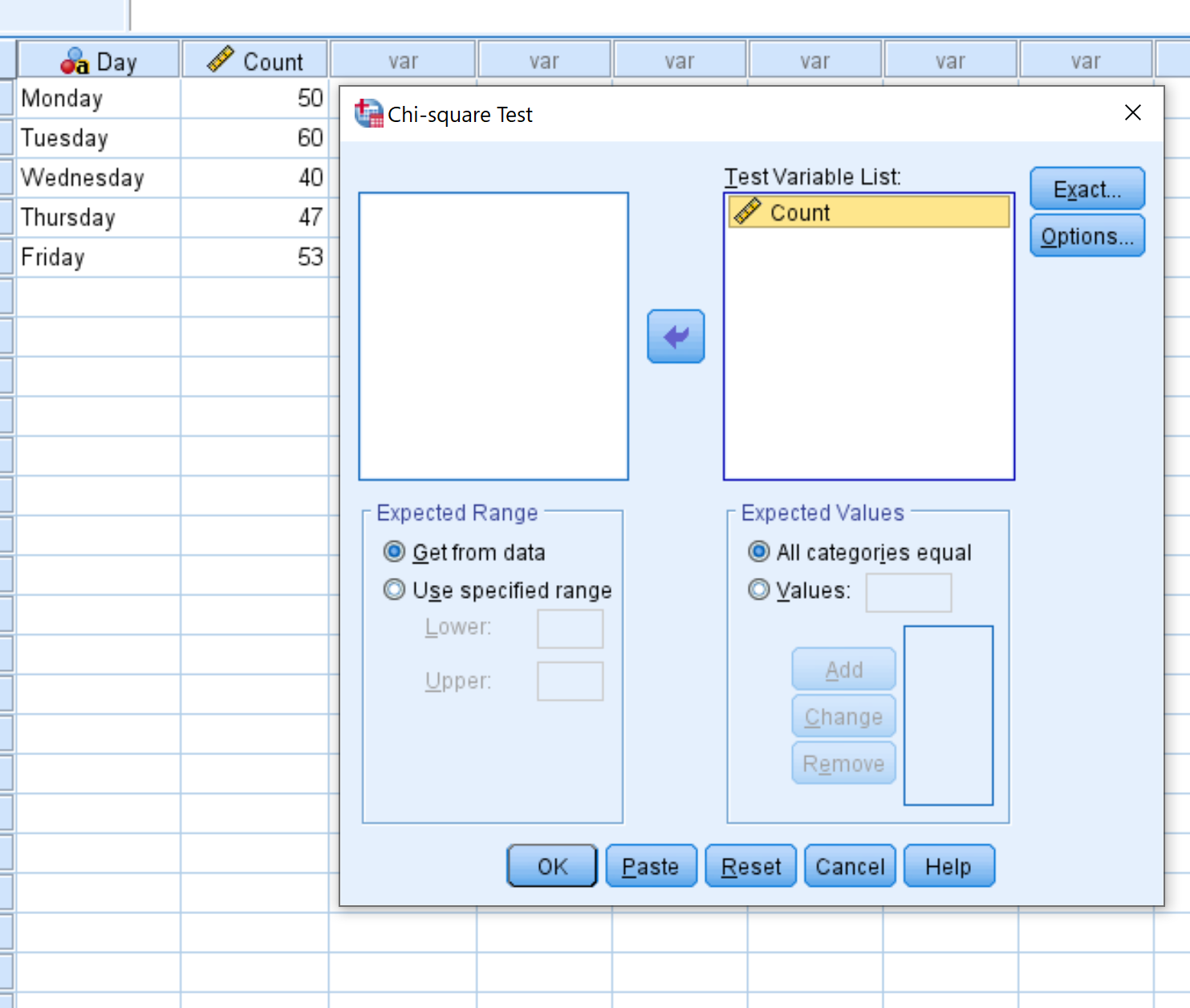
В новом появившемся окне перетащите переменную Count в поле с надписью Test Variable List. Затем нажмите ОК .
Шаг 3: Выполните тест критерия согласия хи-квадрат.
Перейдите на вкладку « Анализ », затем « Непараметрические тесты », затем « Устаревшие диалоги », затем « Хи-квадрат »:
В новом появившемся окне перетащите переменную Count в поле с надписью Test Variable List.
Оставьте метку рядом со всеми категориями одинаковыми , поскольку каждая из наших категорий (т. е. дни недели) имеет одинаковое ожидаемое количество посетителей каждый день. Затем нажмите ОК .

Шаг 4: Интерпретируйте результаты .
После того, как вы нажмете OK , появятся результаты критерия согласия хи-квадрата:
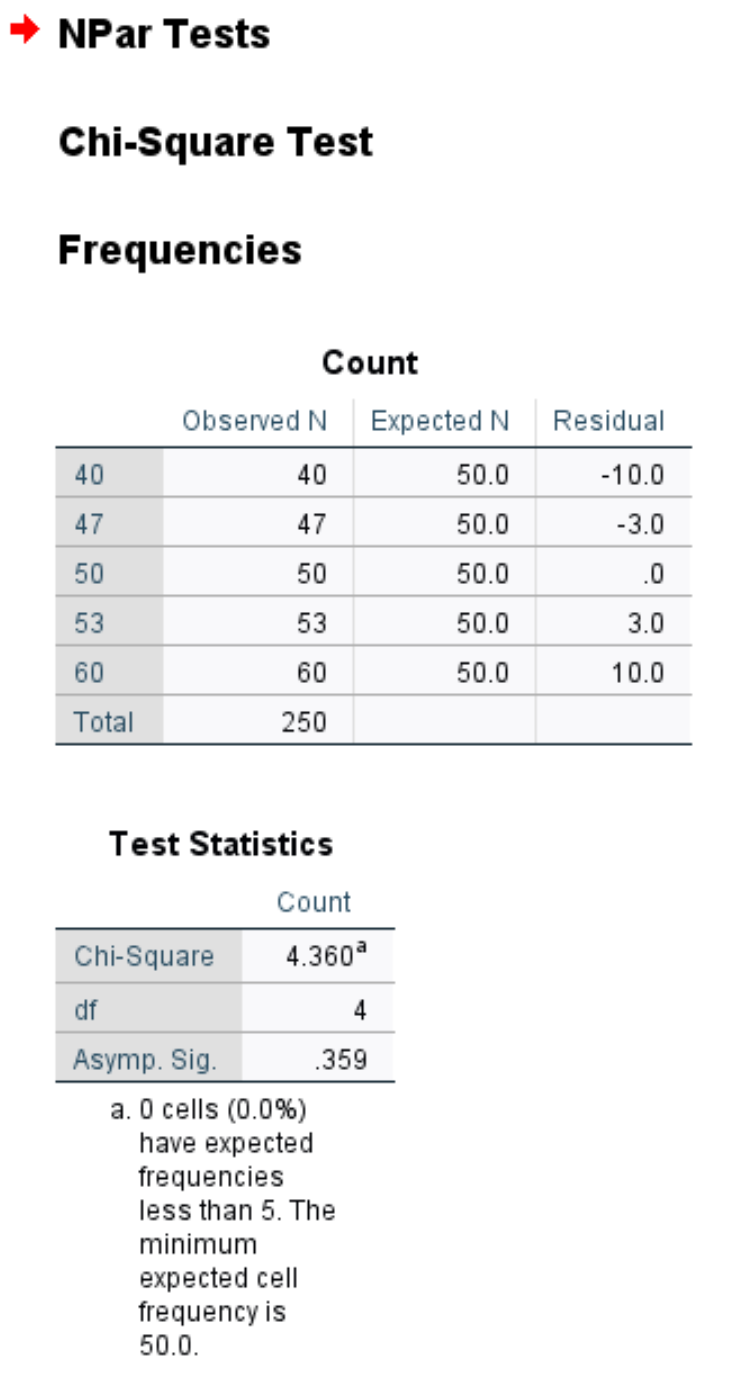
В первой таблице показано наблюдаемое и ожидаемое количество клиентов в каждый день недели, а также остаток (т. е. разница) между наблюдаемым и ожидаемым.
Во второй таблице отображаются следующие числа:
Хи-квадрат: Статистика теста хи-квадрат оказалась равной 4,36.
df: Степени свободы, рассчитанные как #categories-1 = 5-1 = 4.
Асимп. Sig: значение p, соответствующее значению хи-квадрат 4,36 с 4 степенями свободы, оказалось равным 0,359. Это значение также можно найти с помощью калькулятора отношения показателя хи-квадрат к значению P.
Поскольку p-значение (0,359) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что истинное распределение покупателей отличается от распределения, о котором заявил владелец магазина.