Тест Чоу — это статистический тест, разработанный экономистом Грегори Чоу , который используется для проверки равенства коэффициентов в двух разных моделях регрессии на разных наборах данных.
Тест Чоу обычно используется в области эконометрики с данными временных рядов, чтобы определить, есть ли структурный разрыв в данных в какой-то момент.
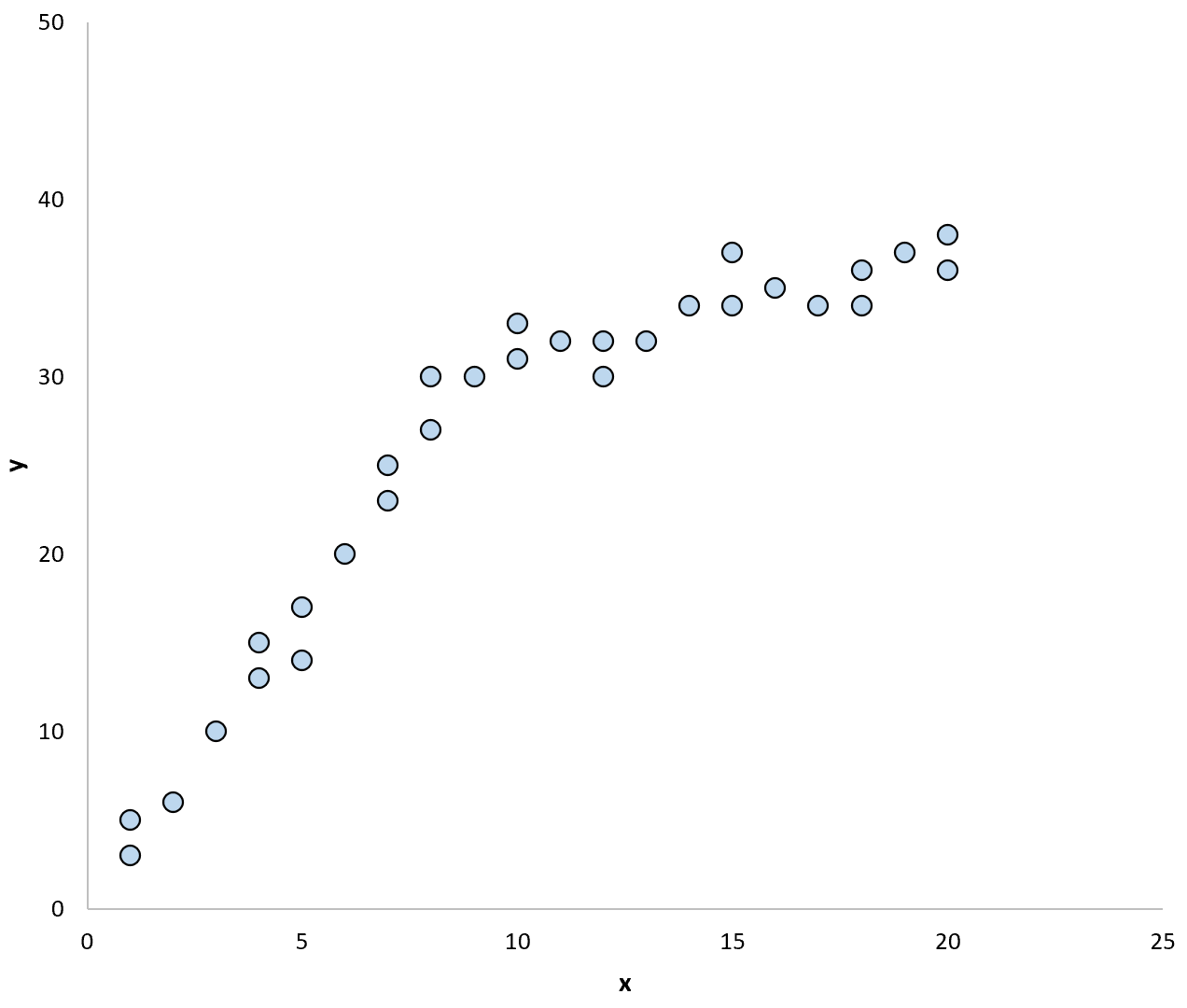
Например, рассмотрим следующую диаграмму рассеяния:
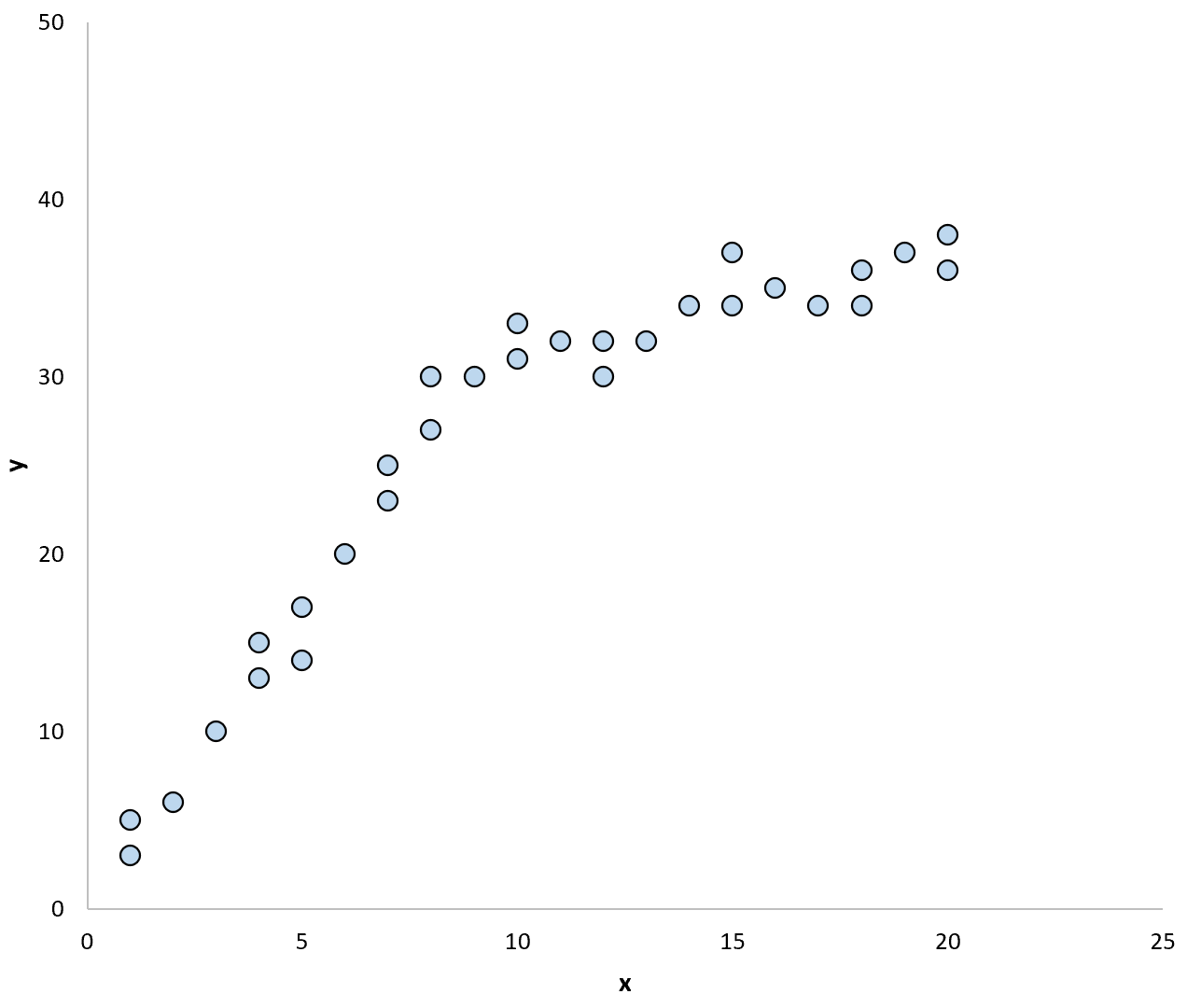
Если бы мы использовали одну линию регрессии для обобщения закономерности в данных, это могло бы выглядеть так:
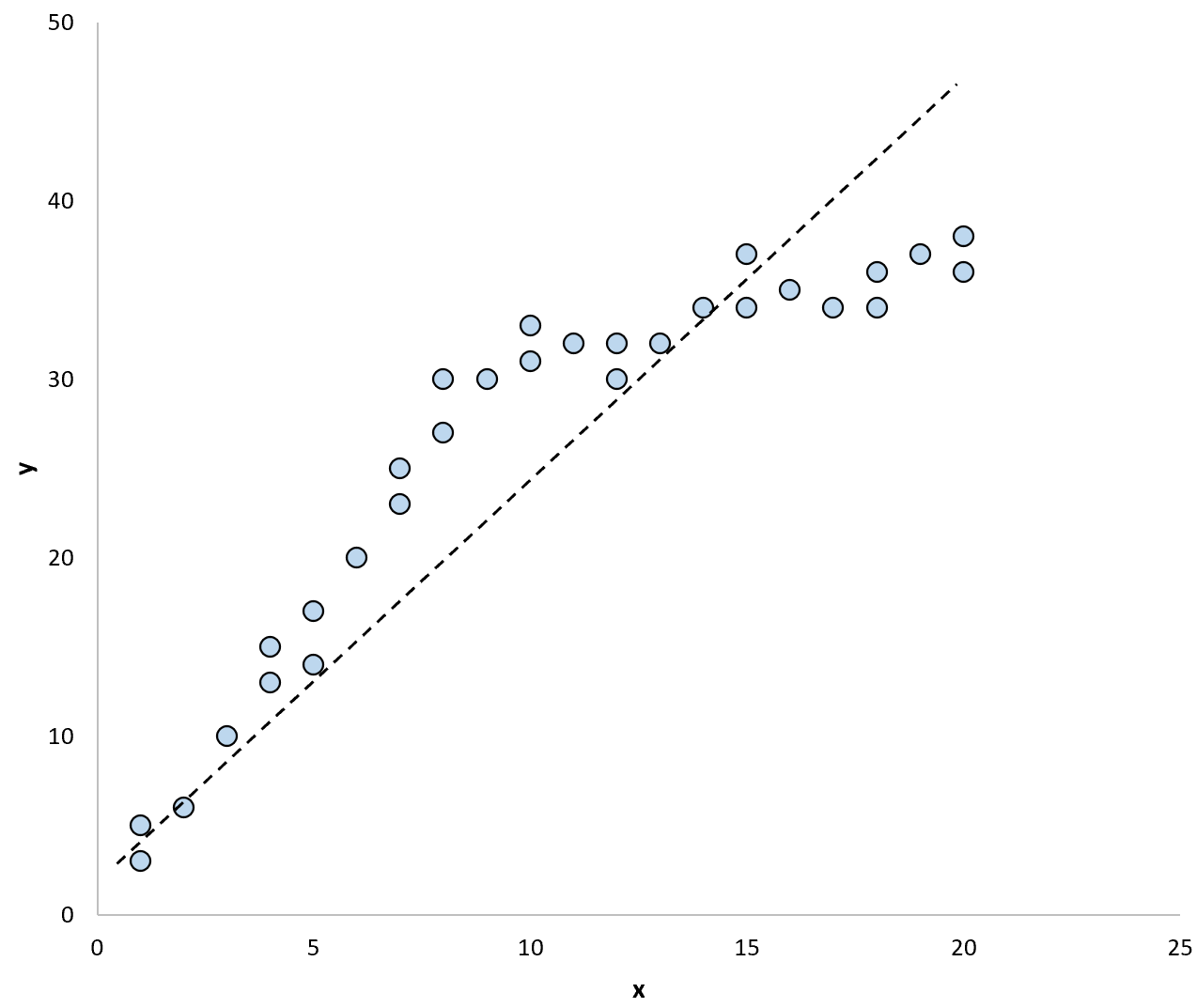
И если бы мы использовали две отдельные линии регрессии, чтобы обобщить закономерность в данных, это могло бы выглядеть так:
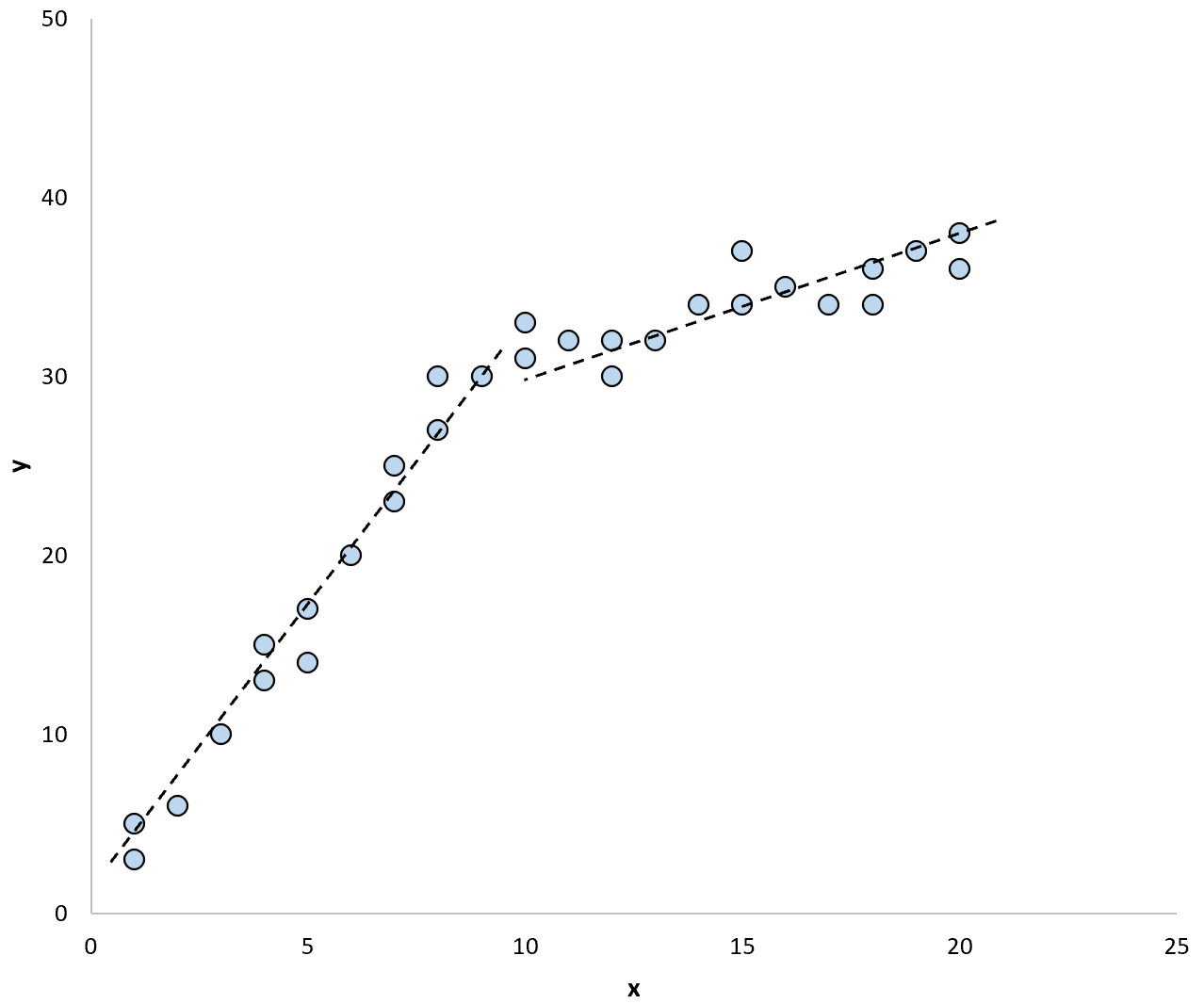
Тест Чоу позволяет нам проверить, равны ли коэффициенты регрессии каждой линии регрессии.
Если тест определяет, что коэффициенты между линиями регрессии не равны, это означает наличие существенных доказательств того, что в данных существует структурный разрыв. Другими словами, структура данных значительно отличается до и после этой структурной точки разрыва.
Когда использовать тест чау-чау
Следующие примеры иллюстрируют ситуации, когда вы можете захотеть выполнить тест Чоу:
1. Определить, меняются ли цены акций с разной скоростью до и после выборов.
2. Определить, изменяются ли цены на жилье до и после изменения процентной ставки.
3. Определить, различается ли средняя прибыль публичных компаний до и после принятия нового закона о налогах.
В каждой ситуации мы могли бы использовать тест Чоу, чтобы определить, есть ли точка структурного разрыва в данных в определенный момент времени.
Шаги для проведения теста чау-чау
Мы можем использовать следующие шаги для выполнения теста Чоу.
Шаг 1: Определите нулевую и альтернативную гипотезы.
Предположим, мы подгоняем следующую модель регрессии ко всему нашему набору данных:
- y t = a + bx 1t + cx t2 + ε
Затем предположим, что мы разделили наши данные на две группы на основе некоторой структурной точки разрыва и подобрали к каждой группе следующие модели регрессии:
- y t = a 1 + b 1 x 1t + c 1 x t2 + ε
- y t = a 2 + b 2 x 1t + c 2 x t2 + ε
Мы будем использовать следующие нулевые и альтернативные гипотезы для теста Чоу:
- Null (H 0 ): a 1 = a 2 , b 1 = b 2 и c 1 = c 2
- Альтернатива ( HA ): по крайней мере одно из сравнений в Null не равно.
Если мы отклоним нулевую гипотезу, у нас будет достаточно доказательств, чтобы сказать, что в данных есть точка структурного разрыва, и две линии регрессии могут соответствовать данным лучше, чем одна.
Если нам не удастся отвергнуть нулевую гипотезу, у нас не будет достаточных доказательств, чтобы сказать, что в данных есть точка структурного разрыва. В этом случае мы говорим, что линии регрессии могут быть «объединены» в одну линию регрессии, которая достаточно хорошо представляет закономерность в данных.
Шаг 2: Рассчитайте тестовую статистику.
Если мы определим следующие термины:
- S T : сумма квадратов остатков от общих данных.
- S 1 , S 2 : сумма квадратов остатков от каждой группы
- N 1 , N 2 : количество наблюдений в каждой группе
- k: количество параметров
Тогда мы можем сказать, что статистика теста Чоу:
Статистика теста Чоу = [(S T – (S 1 +S 2 ))/k] / [(S 1 +S 2 )/(N 1 +N 2 -2k)]
Эта тестовая статистика соответствует F-распределению с k и и N 1 +N 2 -2k степеней свободы.
Шаг 3: Отклонить или не отклонить нулевую гипотезу.
Если p-значение, связанное с этой тестовой статистикой, меньше определенного уровня значимости , мы можем отклонить нулевую гипотезу и сделать вывод, что в данных есть точка структурного разрыва.
К счастью, большинство статистических программ способны выполнять тест Чоу, поэтому вам, скорее всего, никогда не придется выполнять тест вручную.
Пример проведения теста чау-чау
Обратитесь к этому руководству , чтобы увидеть пошаговый пример того, как выполнить тест Чоу для заданного набора данных в R.
Примечания к тесту чау-чау
Вот несколько замечаний, которые следует иметь в виду в отношении теста Чау:
1. Тест предполагает, что остатки регрессионных моделей независимо и одинаково распределены от нормального распределения с неизвестной дисперсией.
2. Тест Чоу следует использовать только тогда, когда структурный сдвиг, который вы хотите проверить, произошел в известное время. Другими словами, тест не следует использовать повторно, чтобы определить, можно ли считать какой-либо момент времени структурным сдвигом.