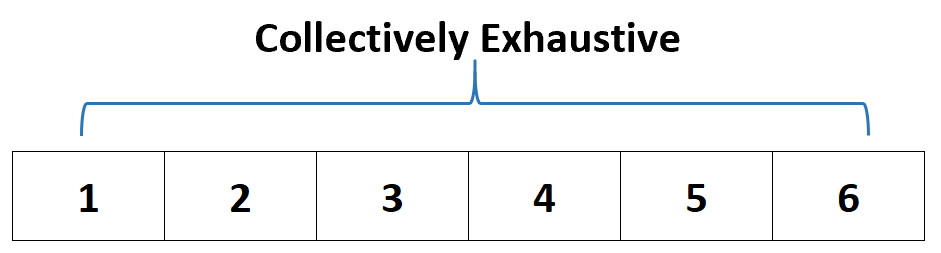
Набор событий считается исчерпывающим , если хотя бы одно из них должно произойти.
Например, если мы бросаем кубик, он должен выпасть на одно из следующих значений:
- 1
- 2
- 3
- 4
- 5
- 6
Таким образом, мы бы сказали, что набор событий {1, 2, 3, 4, 5, 6} в совокупности является исчерпывающим , потому что кость должна выпасть на одно из этих значений.
Другими словами, этот набор событий как совокупность исчерпывает все возможные исходы.
В следующих примерах показаны еще несколько ситуаций, которые иллюстрируют коллективно исчерпывающие события:
Пример 1: подбрасывание монеты
Предположим, мы подбрасываем монету один раз. Мы знаем, что монета должна приземлиться на одно из следующих значений:
- Головы
- хвосты
Таким образом, совокупность событий {Орел, Решка} будет исчерпывающей.
Пример 2: вращение спиннера
Предположим, у нас есть спиннер трех разных цветов: красный, синий и зеленый.

Если мы прокрутим его один раз, он должен приземлиться на одно из следующих значений:
- Красный
- Синий
- Зеленый
Таким образом, совокупность событий {Красный, Синий, Зеленый} будет исчерпывающей.
Однако набор событий {Красный, Зеленый} не будет в совокупности исчерпывающим, поскольку он не содержит всех возможных исходов.
Пример 3: Типы баскетболистов
Предположим, у нас есть опрос, в котором людей просят выбрать их любимую позицию баскетболиста. Единственные возможные ответы:
- Разыгрывающий
- Атакующий защитник
- Легкий форвард
- Могучий форвард
- Центр
Таким образом, набор событий {Разыгрывающий, Атакующий защитник, Легкий форвард, Мощный форвард, Центр} в совокупности будет исчерпывающим.
Однако набор событий {Разыгрывающий, Атакующий защитник, Легкий форвард} в совокупности не будет исчерпывающим, поскольку он не содержит всех возможных исходов.
Важность совокупных исчерпывающих событий в опросах
При разработке опросов особенно важно, чтобы ответы на вопросы были исчерпывающими.
Например, предположим, что в опросе задается следующий вопрос:
Какая ваша любимая позиция баскетболиста?
И предположим, что потенциальные ответы были такими:
- Разыгрывающий
- Атакующий защитник
- Легкий форвард
- Могучий форвард
Поскольку позиция « Центр» была исключена, эти ответы в совокупности не являются исчерпывающими.
Это означает, что тот, кто предпочитает центр в качестве своей любимой позиции, должен будет выбрать один из других вариантов, а это означает, что ответы на опрос не будут отражать истинное мнение респондентов.
Коллективный исчерпывающий или взаимоисключающий
События являются взаимоисключающими , если они не могут произойти одновременно.
Например, пусть событие A будет событием, когда игральная кость выпадет на четное число, а событие B будет событием, когда игральная кость выпадет на нечетное число.
Мы бы определили выборочное пространство для событий следующим образом:
- А = {2, 4, 6}
- В = {1, 3, 5}
Обратите внимание, что между двумя образцами пространств нет перекрытия, что означает, что они взаимоисключающие. В совокупности они также оказываются исчерпывающими, потому что в совокупности они могут учитывать все потенциальные результаты броска кубика.
Однако предположим, что мы определяем событие A и событие B следующим образом:
- А = {1, 2, 3, 4}
- В = {3, 4, 5, 6}
В этом случае между A и B есть некоторое совпадение, поэтому они не исключают друг друга. Тем не менее, вместе взятые, они все же могут объяснить все возможные результаты броска кубика.
Это иллюстрирует важный момент: набор событий может быть в совокупности исчерпывающим, но не исключающим друг друга .