Логистическая регрессия — это тип регрессии, который мы можем использовать, когда переменная ответа является двоичной.
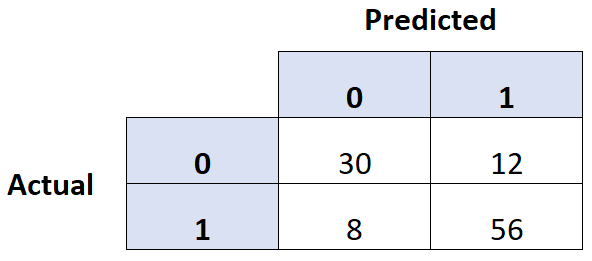
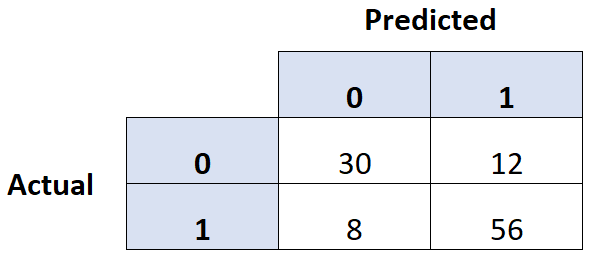
Одним из распространенных способов оценки качества модели логистической регрессии является создание матрицы путаницы , которая представляет собой таблицу 2 × 2, в которой показаны прогнозируемые значения из модели и фактические значения из тестового набора данных.
В следующем пошаговом примере показано, как создать матрицу путаницы в R.
Шаг 1: Подберите модель логистической регрессии
В этом примере мы будем использовать набор данных по умолчанию из пакета ISLR.Мы будем использовать статус студента, остаток на банковском счете и годовой доход, чтобы предсказать вероятность того, что данное лицо не выполнит свои обязательства по кредиту.
В следующем коде показано, как подогнать модель логистической регрессии к этому набору данных:
#load necessary packages
library (caret)
library (InformationValue)
library (ISLR)
#load dataset
data <- Default
#split dataset into training and testing set
set. seed (1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace= TRUE , prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]
#fit logistic regression model
model <- glm(default~student+balance+income, family=" binomial", data=train)
Шаг 2: Создайте матрицу путаницы
Далее мы воспользуемся функцией путаницыMatrix() из пакета каретки , чтобы
#use model to predict probability of default
predicted <- predict(model, test, type="response")
#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default==" Yes", 1, 0)
#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]
#create confusion matrix
confusionMatrix(test$default, predicted)
0 1
0 2912 64
1 21 39
Шаг 3: Оцените матрицу путаницы
Мы также можем рассчитать следующие показатели, используя матрицу путаницы:
- Чувствительность: «истинно положительный показатель» — процент лиц, правильно предсказанных моделью, которые не выполнят свои обязательства.
- Специфичность: «Истинно отрицательный показатель» — процент лиц, правильно предсказанных моделью, которые не будут дефолтными.
- Общий коэффициент ошибочной классификации: процент от общего числа неправильных классификаций, сделанных моделью.
В следующем коде показано, как рассчитать эти показатели:
#calculate sensitivity
sensitivity(test$default, predicted)
[1] 0.3786408
#calculate specificity
specificity(test$default, predicted)
[1] 0.9928401
#calculate total misclassification error rate
misClassError(test$default, predicted, threshold =optimal)
[1] 0.027
Общая частота ошибок неправильной классификации составляет 2,7% для этой модели.
В общем, чем ниже этот показатель, тем лучше модель способна предсказывать результаты, поэтому эта конкретная модель оказывается очень хорошей в предсказании того, будет ли человек дефолтным или нет.