Коэффициент корреляции Пирсона измеряет линейную связь между двумя переменными.
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Формула для расчета коэффициента корреляции Пирсона, обозначаемая r , выглядит следующим образом:

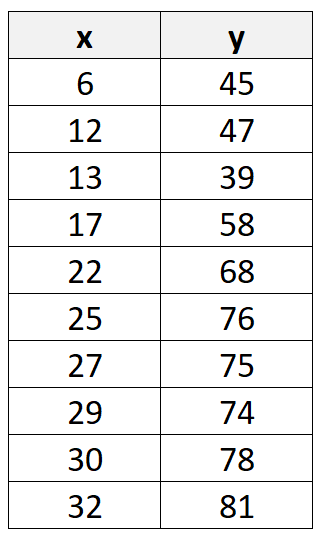
Источник: Википедия В этом руководстве представлен пошаговый пример того, как вручную рассчитать коэффициент корреляции Пирсона для следующего набора данных:
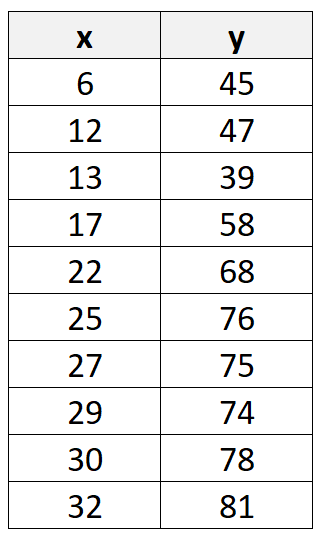
Шаг 1: вычислить среднее значение X и Y
Сначала мы вычислим среднее значение значений X и Y:
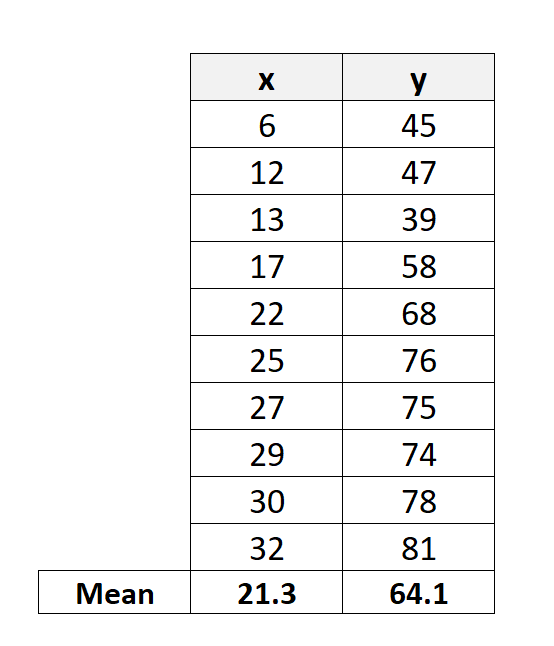
Шаг 2: Рассчитайте разницу между средними значениями
Далее мы рассчитаем разницу между каждым из отдельных значений X и Y и их соответствующими средними значениями:
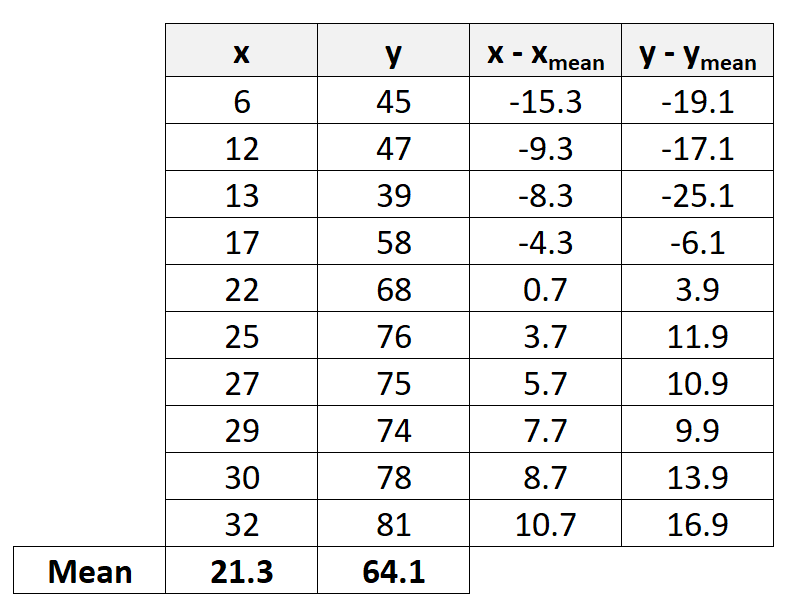
Шаг 3: Рассчитайте оставшиеся значения
Далее мы рассчитаем оставшиеся значения, необходимые для завершения формулы коэффициента корреляции Пирсона:
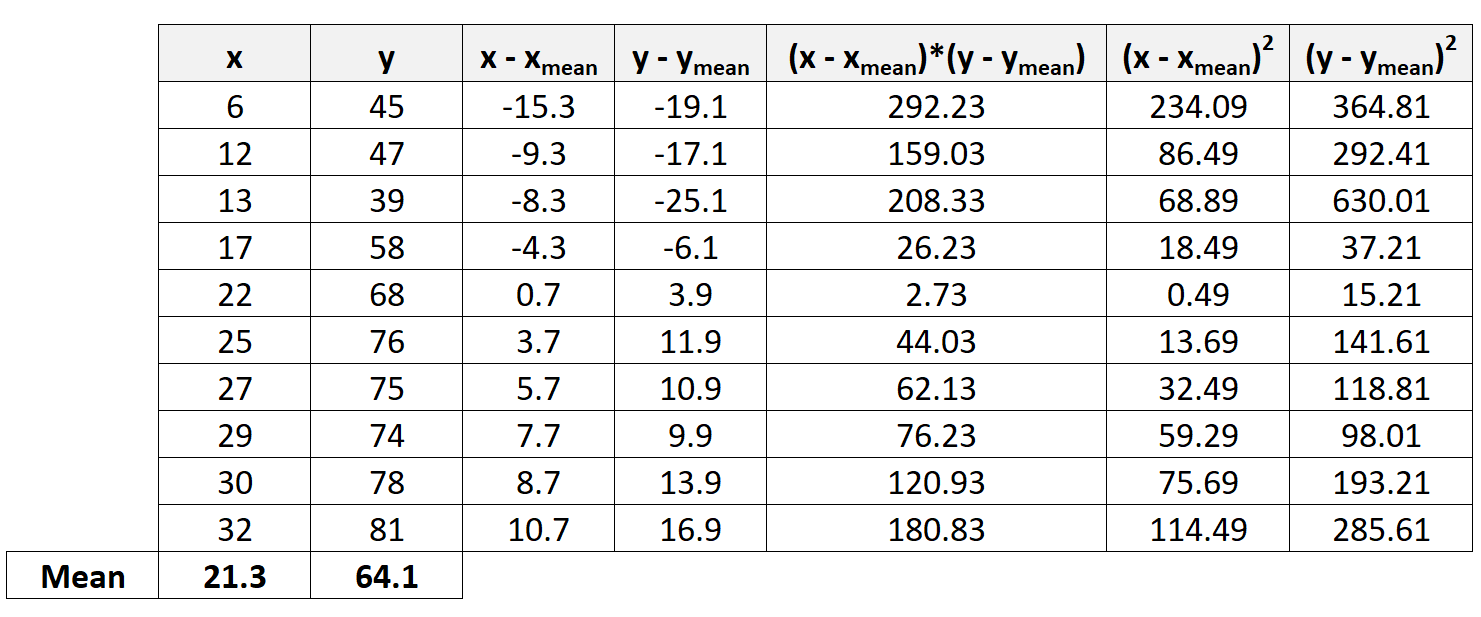
Шаг 4: Рассчитайте суммы
Далее мы вычислим суммы последних трех столбцов:
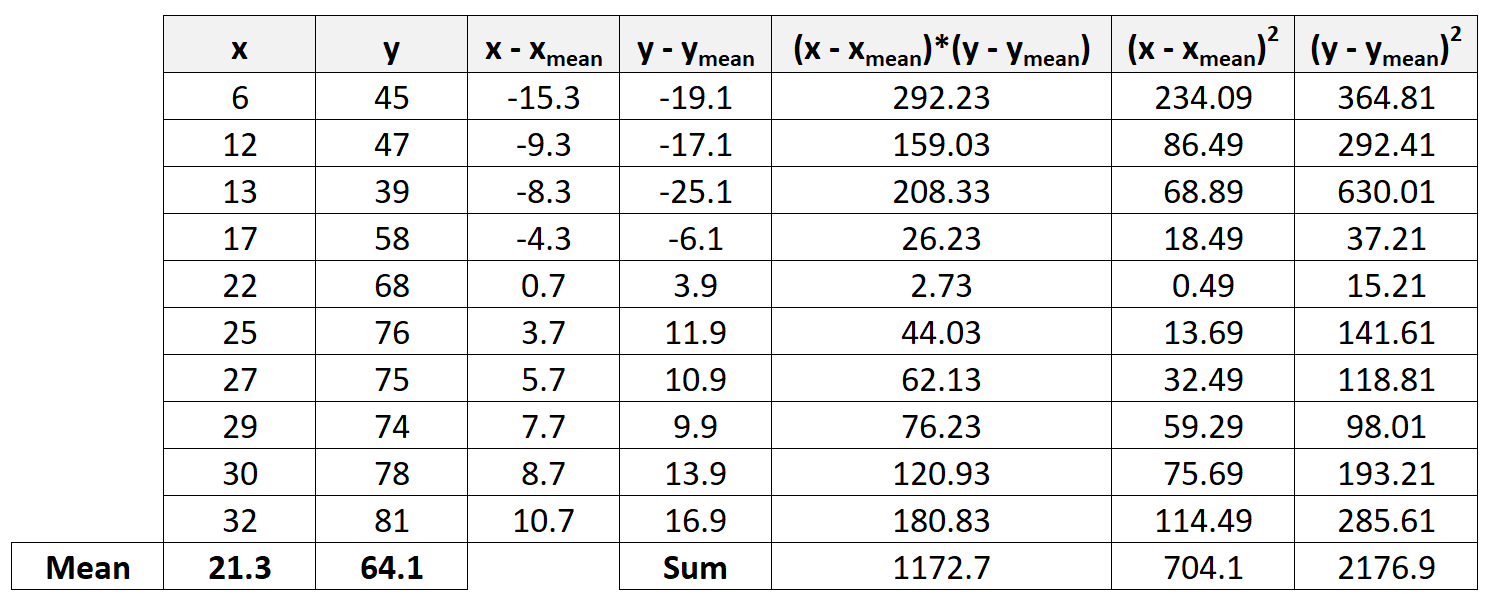
Шаг 5. Рассчитайте коэффициент корреляции Пирсона.
Теперь мы просто подставим суммы из предыдущего шага в формулу коэффициента корреляции Пирсона:
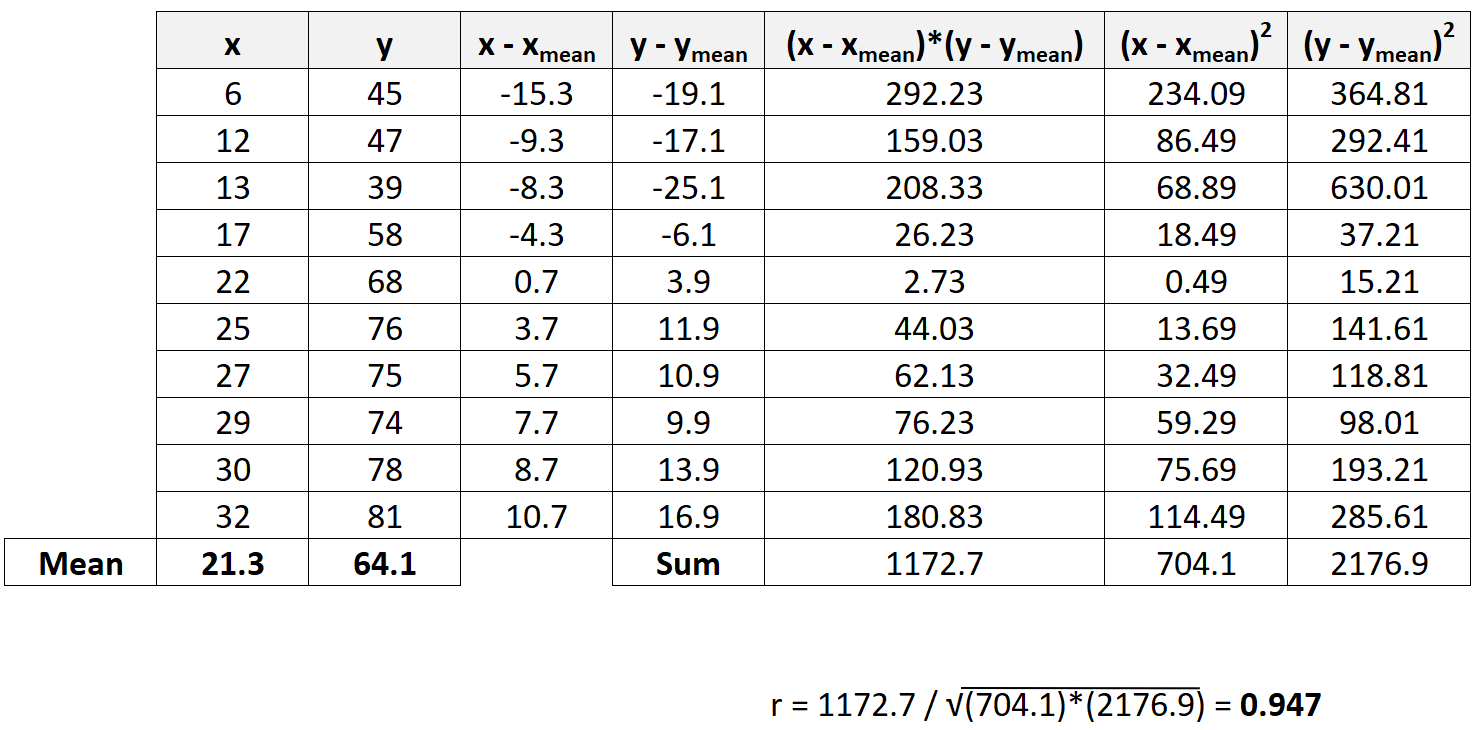
Коэффициент корреляции Пирсона оказывается равным 0,947 .
Поскольку это значение близко к 1, это свидетельствует о сильной положительной корреляции X и Y.
Другими словами, по мере увеличения значения X значение Y также увеличивается весьма предсказуемым образом.
Дополнительные ресурсы
Введение в коэффициент корреляции Пирсона
Как найти доверительный интервал для коэффициента корреляции