Матрица корреляции — это квадратная таблица, которая показываеткоэффициенты корреляции между переменными в наборе данных.
Он предлагает быстрый способ понять силу линейных отношений, существующих между переменными в наборе данных.
Существует четыре распространенных способа создания корреляционной матрицы в R:
Метод 1: функция cor (для получения простой матрицы коэффициентов корреляции)
cor(df)
Метод 2: Функция rcorr (для получения p-значений коэффициентов корреляции)
library (Hmisc)
rcorr(as.matrix(df))
Метод 3: функция corrplot (для визуализации матрицы корреляции)
library (corrplot)
corrplot(cor(df))
Метод 4: Функция ggcorrplot (для визуализации матрицы корреляции)
library (ggcorrplot)
ggcorrplot(cor(df))
В следующих примерах показано, как использовать каждый метод со следующим фреймом данных в R:
#create data frame
df <- data.frame(assists=c(4, 5, 5, 6, 7, 8, 8, 10),
rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
points=c(22, 24, 26, 26, 29, 32, 20, 14))
#view data frame
df
assists rebounds points
1 4 12 22
2 5 14 24
3 5 13 26
4 6 7 26
5 7 8 29
6 8 8 32
7 8 9 20
8 10 13 14
Пример 1: функция cor
Мы можем использовать функцию cor() из базы R, чтобы создать матрицу корреляции, которая показывает коэффициенты корреляции между каждой переменной в нашем фрейме данных:
#create correlation matrix
cor(df)
assists rebounds points
assists 1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608 1.0000000 -0.5220917
points -0.3295730 -0.5220917 1.0000000
Все коэффициенты корреляции по диагонали таблицы равны 1, потому что каждая переменная полностью коррелирует сама с собой.
Все остальные коэффициенты корреляции указывают на корреляцию между различными попарными комбинациями переменных. Например:
- Коэффициент корреляции между передачами и подборами равен -0,245 .
- Коэффициент корреляции между передачами и очками равен -0,330 .
- Коэффициент корреляции между подборами и очками равен -0,522 .
Пример 2: Функция rcorr
Мы можем использовать функцию rcorr() из пакета Hmisc в R, чтобы создать матрицу корреляции, которая показывает коэффициенты корреляции между каждой переменной в нашем фрейме данных:
library (Hmisc)
#create matrix of correlation coefficients and p-values
rcorr(as.matrix(df))
assists rebounds points
assists 1.00 -0.24 -0.33
rebounds -0.24 1.00 -0.52
points -0.33 -0.52 1.00
n= 8
P
assists rebounds points
assists 0.5589 0.4253
rebounds 0.5589 0.1844
points 0.4253 0.1844
Первая матрица показывает коэффициенты корреляции между переменными, а вторая матрица показывает соответствующие p-значения.
Например, коэффициент корреляции между передачами и подборами равен -0,24 , а p-значение для этого коэффициента корреляции равно 0,5589 .
Это говорит нам о том, что корреляция между двумя переменными является отрицательной, но это не является статистически значимой корреляцией, поскольку значение p не менее 0,05.
Пример 3: Функция corpplot
Мы можем использовать функцию corrplot() из пакета corrplot в R, чтобы визуализировать матрицу корреляции:
library (corrplot)
#visualize correlation matrix
corrplot(cor(df))
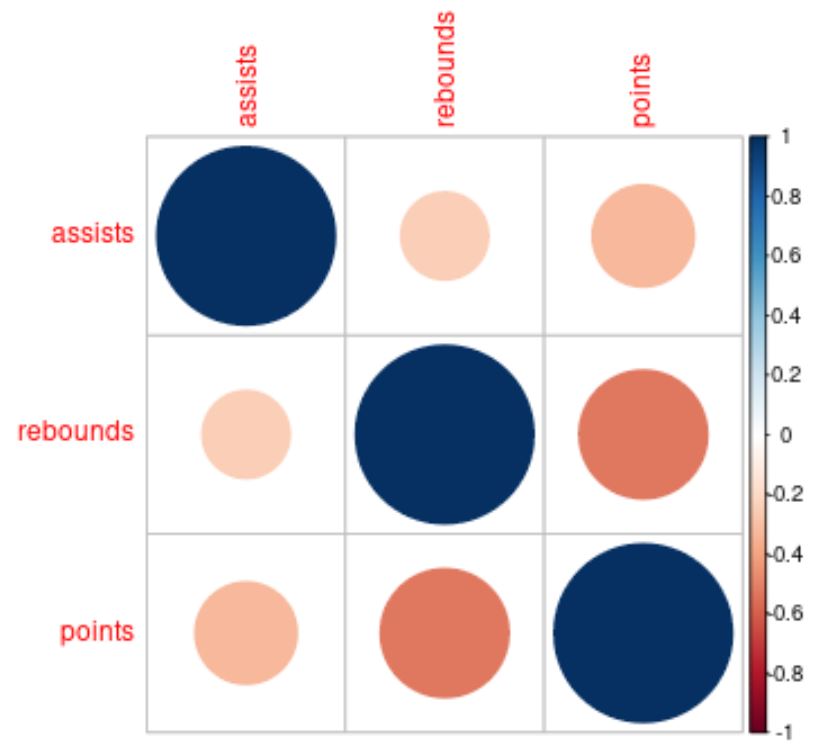
Цвет и размер кругов в матрице корреляции помогают нам визуализировать корреляции между каждой переменной.
Например, круг, в котором пересекаются переменные передач и подборов, маленький и светло-красный, что говорит нам о низкой и отрицательной корреляции.
Пример 4: Функция corpplot
Мы можем использовать функцию ggcorrplot() из пакета ggcorrplot в R для визуализации корреляционной матрицы:
library (ggcorrplot)
#visualize correlation matrix
ggcorrplot(cor(df))
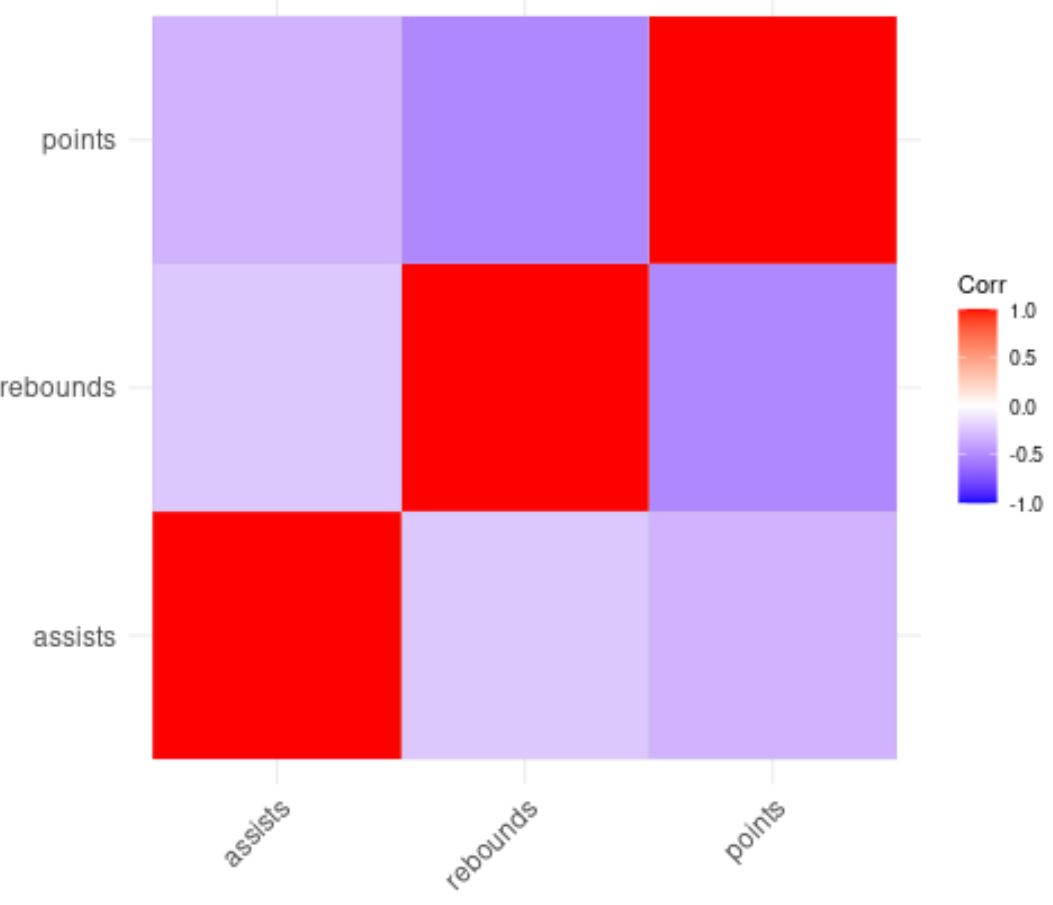
Цвет квадратов в матрице корреляции помогает нам визуализировать корреляции между каждой переменной.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как рассчитать ранговую корреляцию Спирмена в R
Как рассчитать частичную корреляцию в R
Как рассчитать скользящую корреляцию в R