Матрица корреляции — это квадратная таблица, которая показывает коэффициенты корреляции Пирсона между различными переменными в наборе данных.
Напомним, чтокоэффициент корреляции Пирсона — это мера линейной связи между двумя переменными . Он принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в SPSS.
Пример: Как создать матрицу корреляции в SPSS
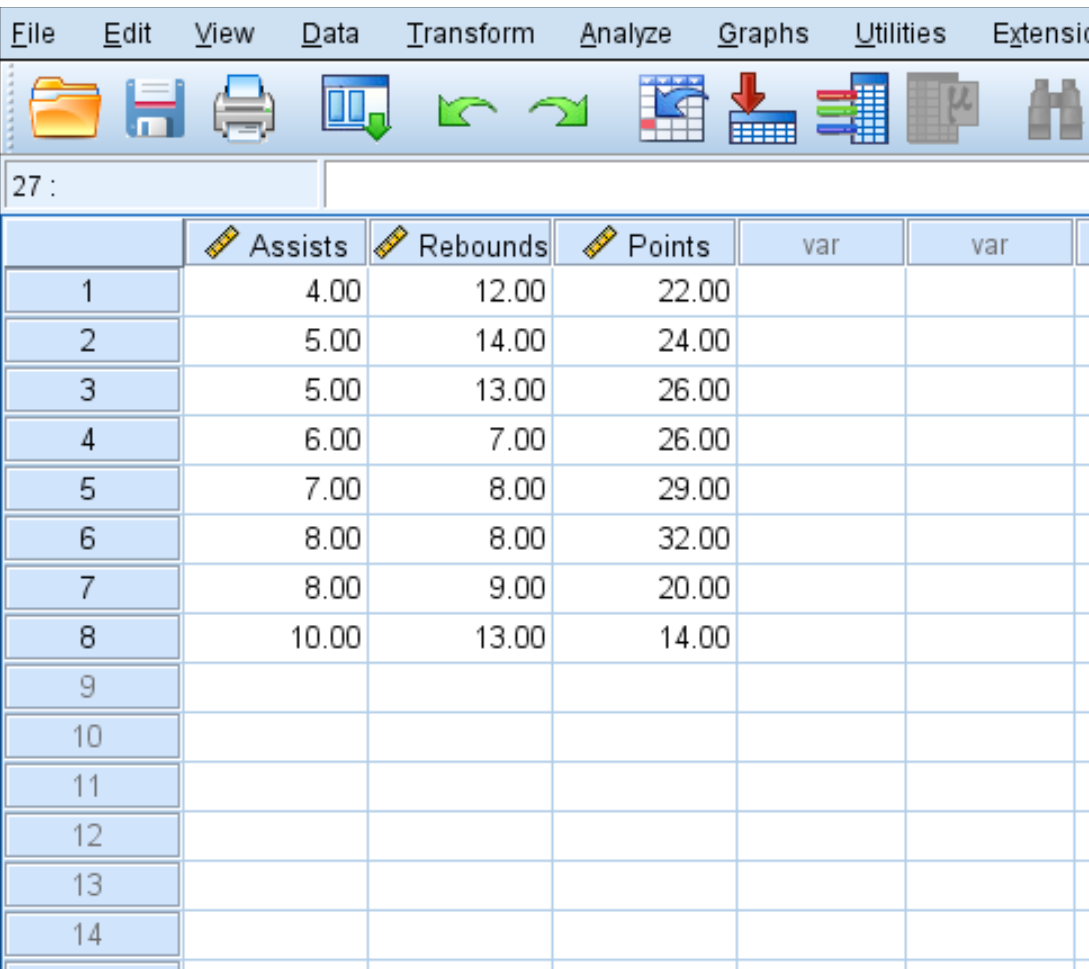
Используйте следующие шаги, чтобы создать матрицу корреляции для этого набора данных, которая показывает средние передачи, подборы и очки для восьми баскетболистов:
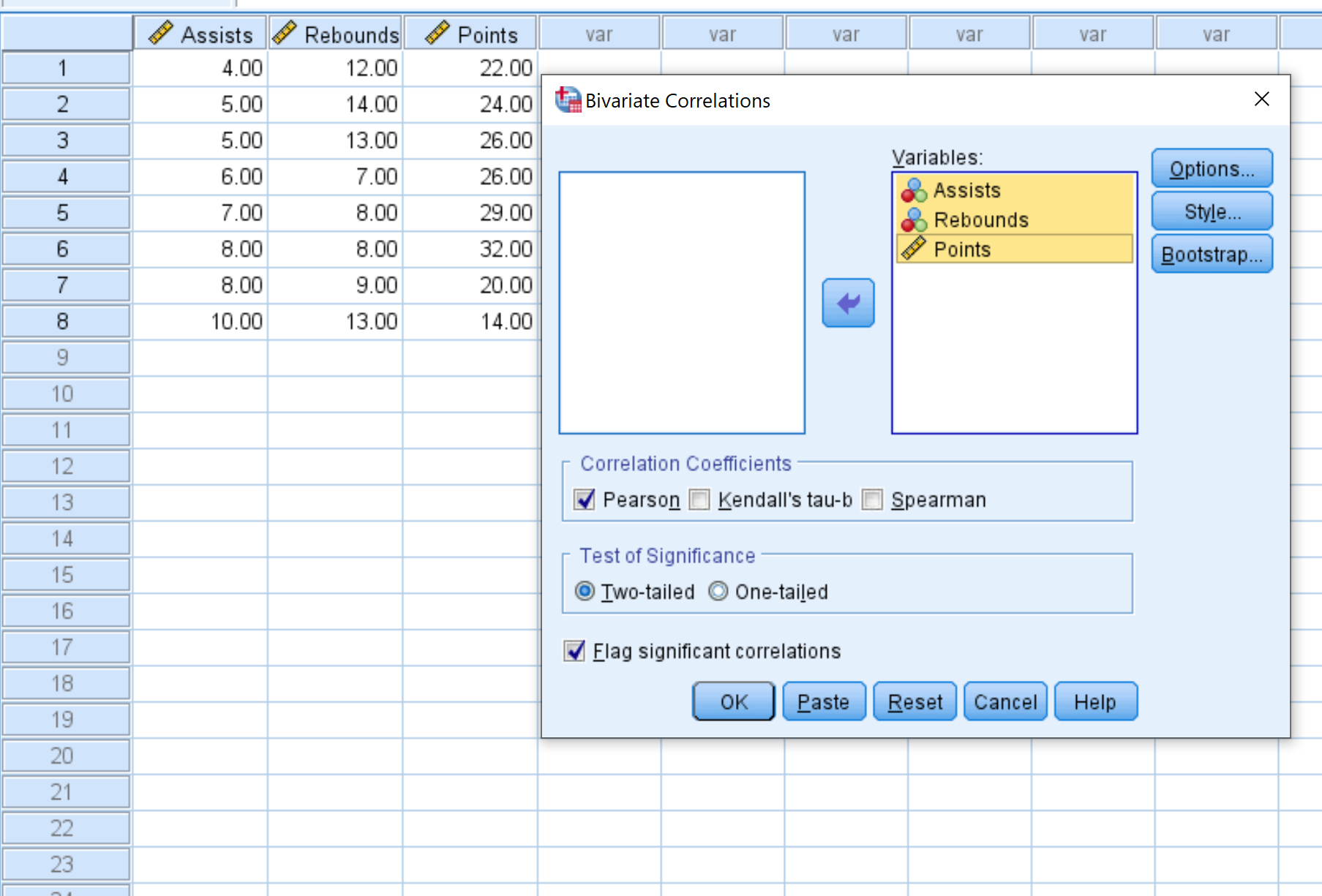
Шаг 1: Выберите двумерную корреляцию.
- Щелкните вкладку Анализ .
- Щелкните Сопоставить .
- Щелкните Двумерный .
Шаг 2: Создайте матрицу корреляции.
Каждая переменная в наборе данных первоначально будет показана в поле слева:
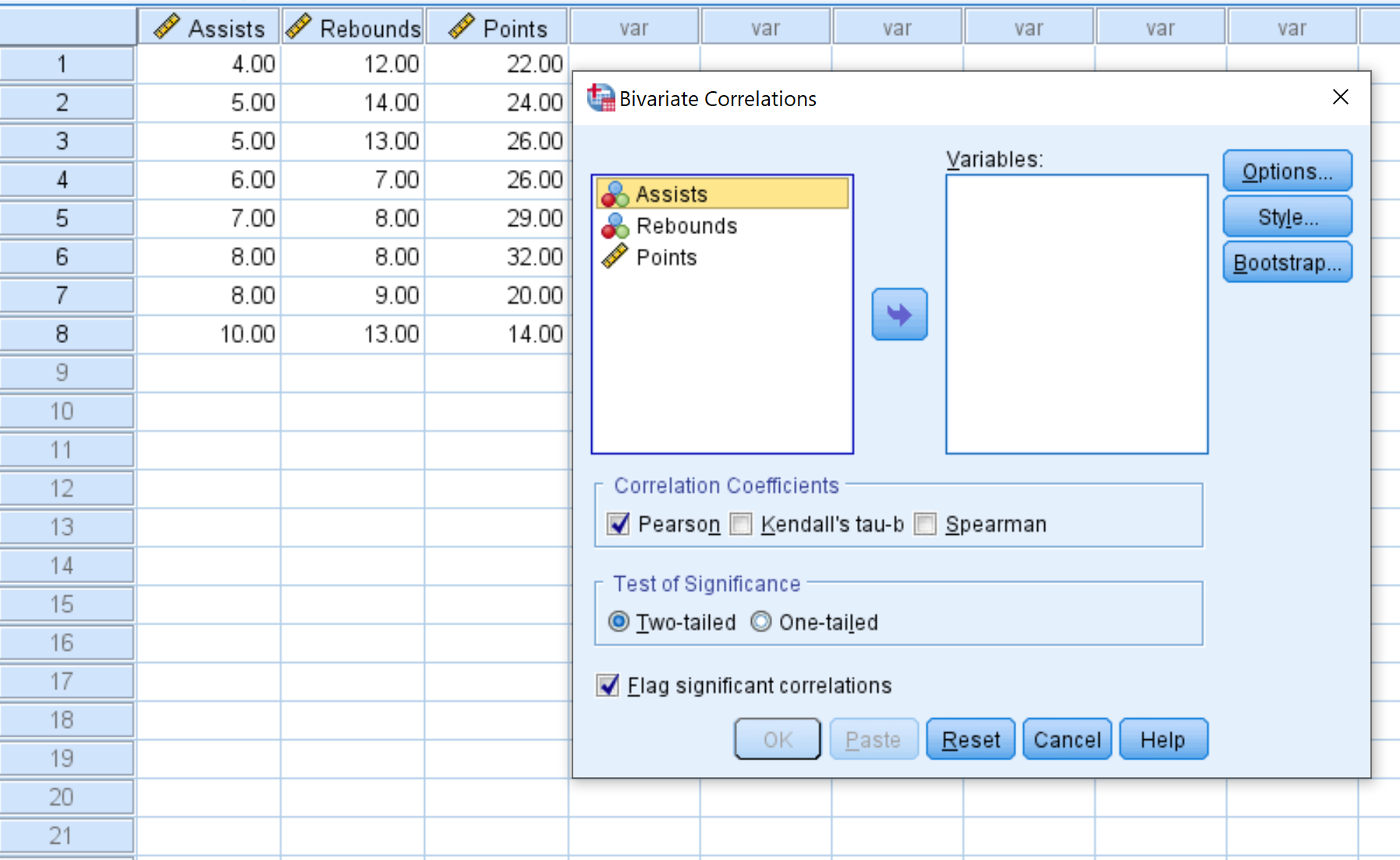
- Выберите каждую переменную, которую вы хотите включить в матрицу корреляции, и щелкните стрелку, чтобы перенести их в поле « Переменные ». В этом примере мы будем использовать все три переменные.
- В разделе Коэффициенты корреляции выберите, хотите ли вы использовать корреляцию Пирсона, тау Кендалла или Спирмена. Мы оставим его как Pearson для этого примера.
- В разделе Проверка значимости выберите, следует ли использовать двусторонний или односторонний тест, чтобы определить, имеют ли две переменные статистически значимую связь. Мы оставим его как Двухвостого.
- Установите флажок рядом с Отметить существенные корреляции , если вы хотите, чтобы SPSS помечал переменные со значительной корреляцией.
- Наконец, нажмите ОК .
После того, как вы нажмете OK , появится следующая матрица корреляции:
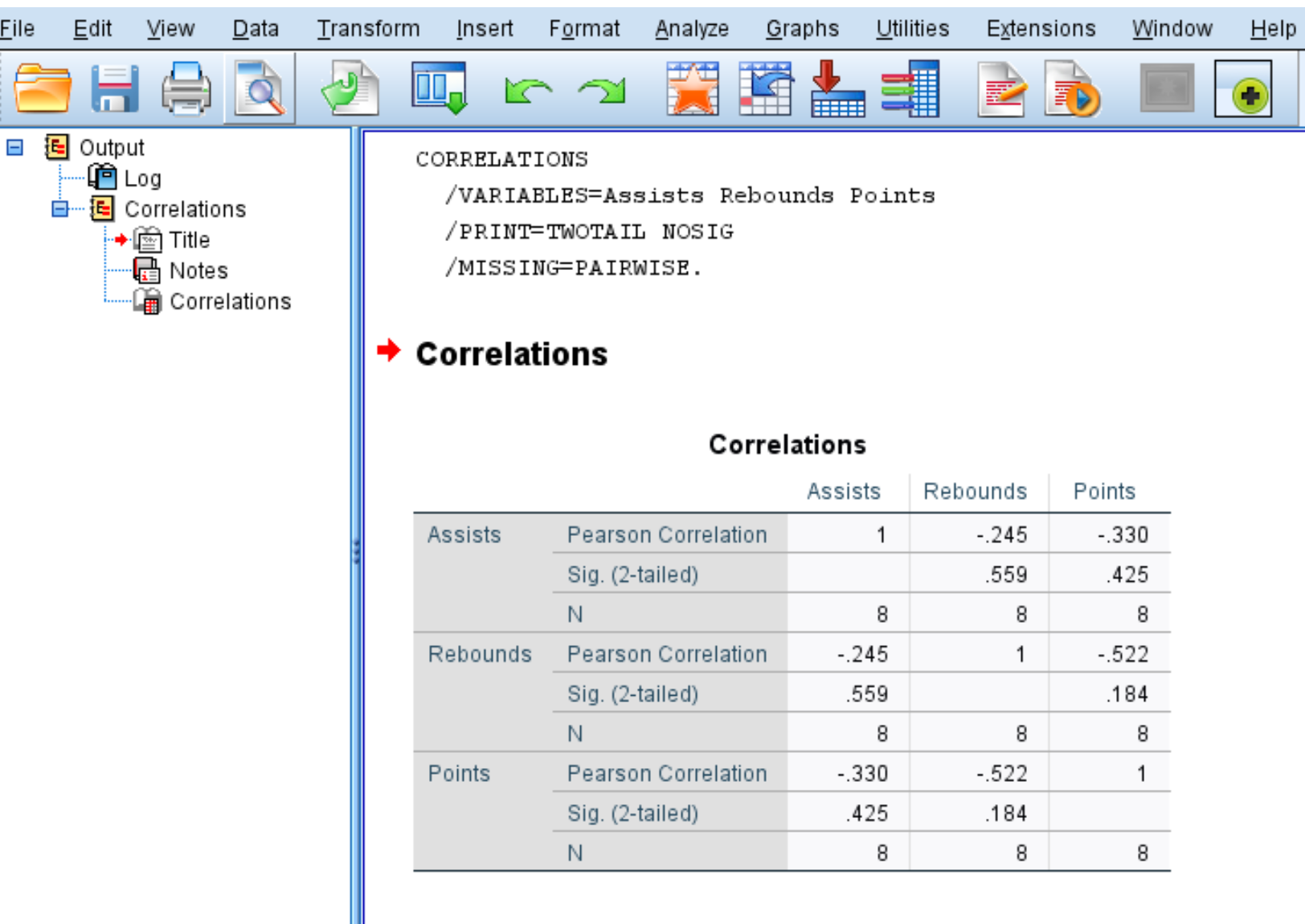
Шаг 3: Интерпретируйте матрицу корреляции.
Матрица корреляции отображает следующие три показателя для каждой переменной:
- Корреляция Пирсона: мера линейной связи между двумя переменными в диапазоне от -1 до 1.
- Сиг. (2-стороннее): двустороннее значение p, связанное с коэффициентом корреляции. Это говорит вам, имеют ли две переменные статистически значимую связь (например, если p < 0,05).
- N: количество пар, используемых для расчета коэффициента корреляции Пирсона.
Например, вот как интерпретировать вывод переменной Assists:
- Коэффициент корреляции Пирсона между передачами и подборами составляет -0,245.Поскольку это число отрицательное, это означает, что эти две переменные имеют отрицательную связь.
- Значение p, связанное с коэффициентом корреляции Пирсона для передач и подборов, составляет 0,559.Поскольку это значение не менее 0,05, две переменные не имеют статистически значимой связи.
- Количество пар, использованных для расчета коэффициента корреляции Пирсона, равнялось 8 (например, в этом расчете использовалось 8 пар игроков).
Шаг 4: Визуализируйте матрицу корреляции.
Вы также можете создать матрицу диаграммы рассеяния, чтобы визуализировать линейную зависимость между каждой из переменных.
- Щелкните вкладку Графики .
- Нажмите Построитель диаграмм .
- Чтобы выбрать тип диаграммы, щелкните Точечная/точечная .
- Щелкните изображение с надписью Матрица рассеяния .
- В поле « Переменные » в левом верхнем углу, удерживая Ctrl, щелкните все три имени переменных. Перетащите их в поле в нижней части диаграммы с надписью Scattermatrix .
- Наконец, нажмите ОК .
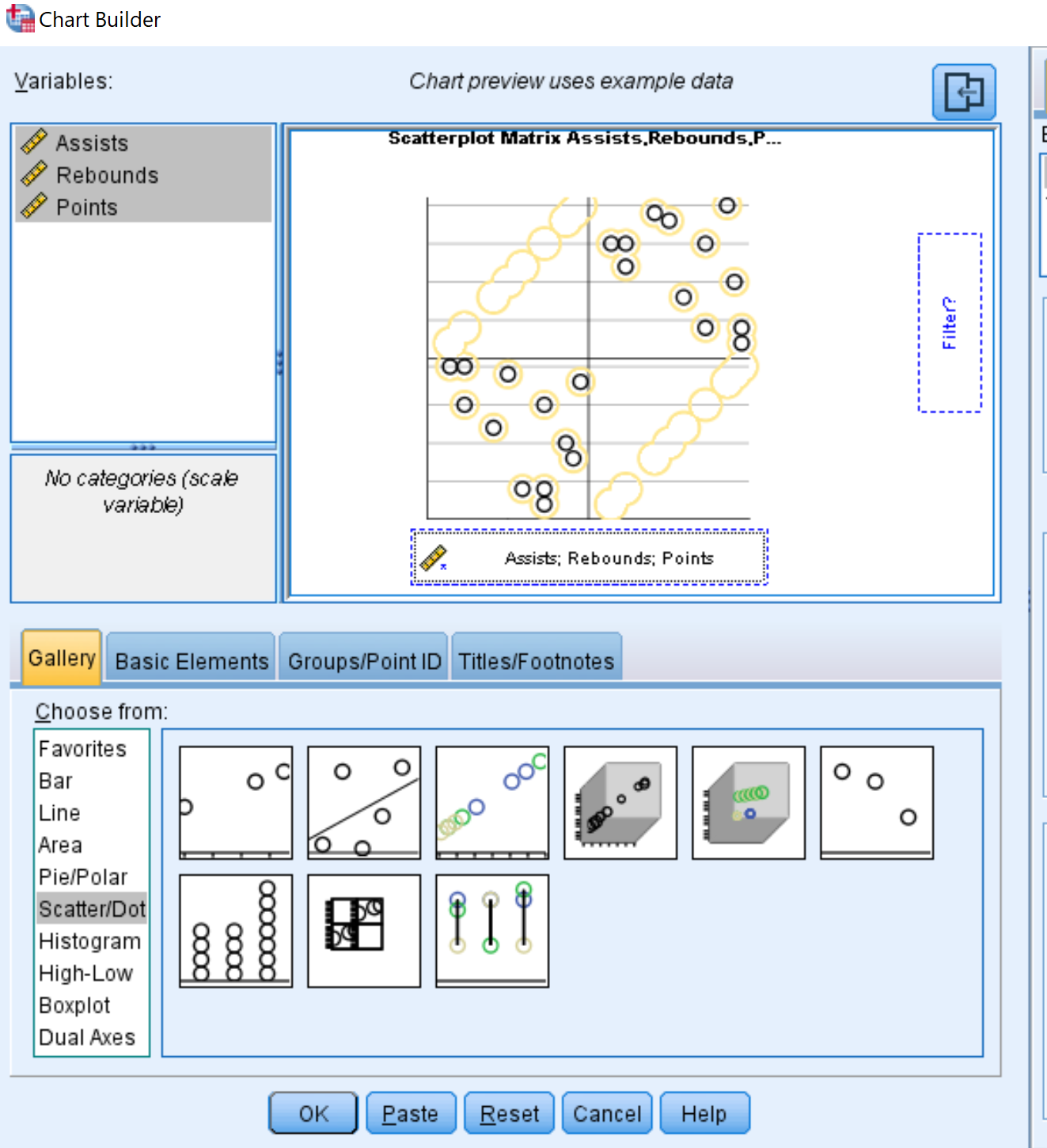
Автоматически появится следующая матрица диаграммы рассеяния:
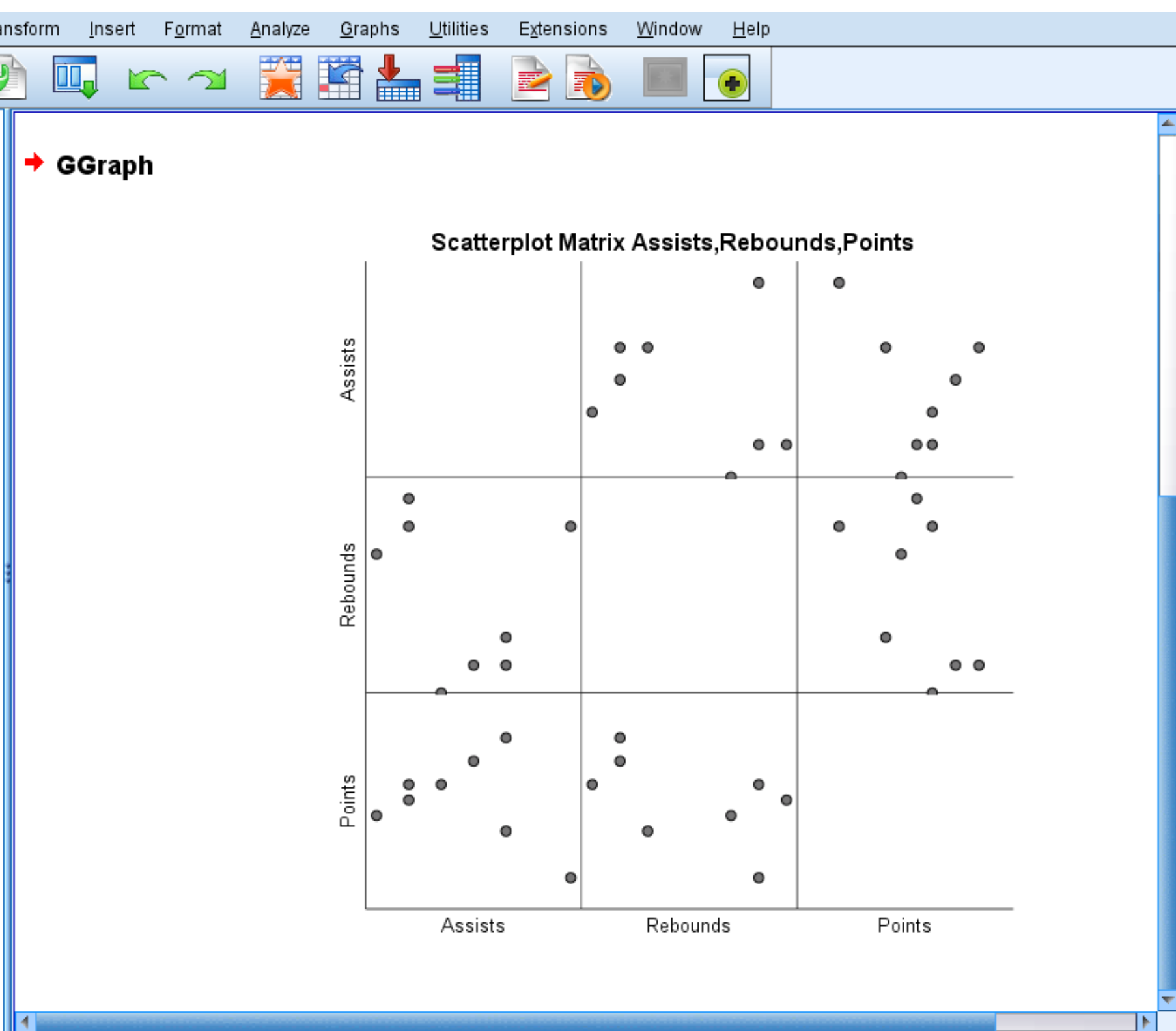
Каждая отдельная диаграмма рассеяния показывает попарные комбинации между двумя переменными. Например, диаграмма рассеяния в левом нижнем углу показывает попарные комбинации очков и передач для каждого из 8 игроков в наборе данных.
Матрица диаграммы рассеяния не является обязательной, но она предлагает хороший способ визуализировать взаимосвязь между каждой парной комбинацией переменных в наборе данных.