Предполагая, что у нас есть вектор A с элементами (A 1 , A 2 , A 3 ) и вектор B с элементами (B 1 , B 2 , B 3 ), мы можем вычислить векторное произведение этих двух векторов как:
Перекрестное произведение = [(A 2 *B 3 ) - (A 3 *B 2 ), (A 3 *B 1 ) - (A 1 *B 3 ), (A 1 *B 2 ) - (A 2 *B 1 )]
Например, предположим, что у нас есть следующие векторы:
- Вектор А: (1, 2, 3)
- Вектор B: (4, 5, 6)
Мы могли бы вычислить векторное произведение этих векторов как:
- Перекрестное произведение = [(A 2 *B 3 ) - (A 3 *B 2 ), (A 3 *B 1 ) - (A 1 *B 3 ), (A 1 *B 2 ) - (A 2 *B 1 )]
- Кросс-произведение = [(2*6) – (3*5), (3*4) – (1*6), (1*5) – (2*4)]
- Перекрестное произведение = (-3, 6, -3)
В следующем примере показано, как вычислить это точное перекрестное произведение в Excel.
Пример: вычисление векторного произведения в Excel
Чтобы вычислить векторное произведение между двумя векторами в Excel, мы сначала введем значения для каждого вектора:

Далее мы вычислим первое значение векторного произведения:

Затем вычислим второе значение:

Наконец, мы вычислим третье значение:

Перекрестное произведение оказывается (-3, 6, -3).
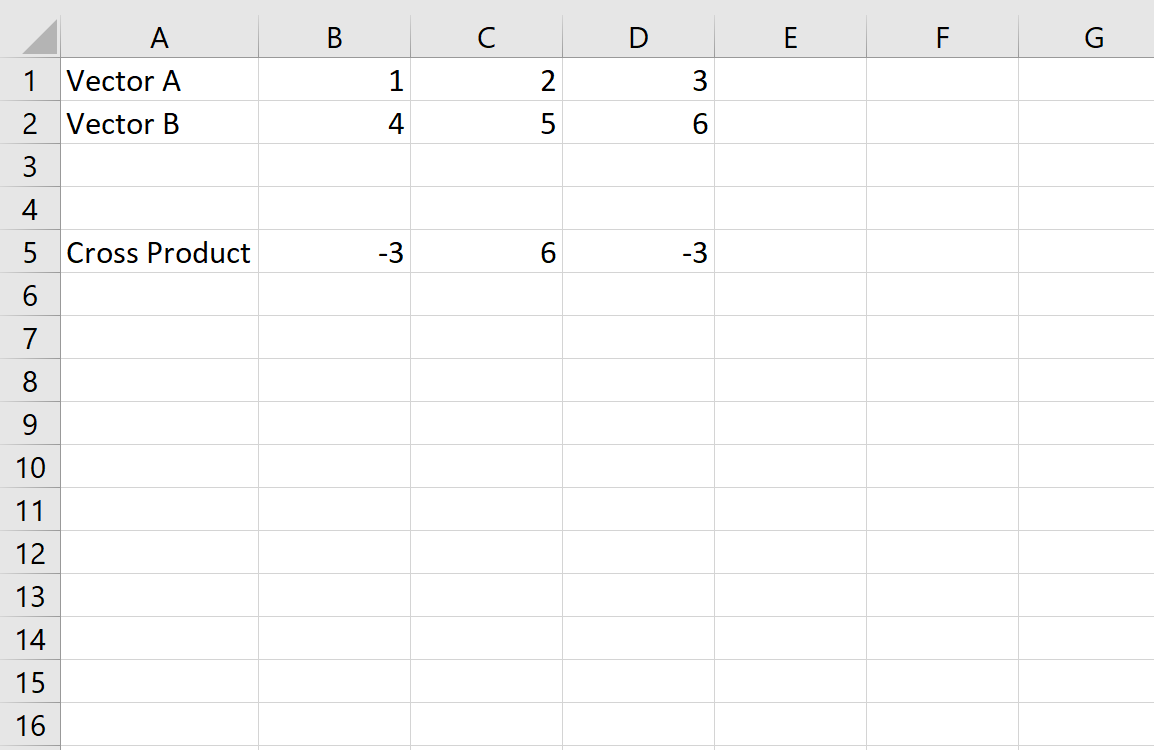
Это соответствует перекрестному произведению, которое мы вычислили ранее вручную.
Дополнительные ресурсы
Как рассчитать скалярный продукт в Excel
Как рассчитать скалярный продукт на калькуляторе TI-84


