Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:
а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3
Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:
а · б = 2*4 + 5*3 + 6*2
а · б = 8 + 15 + 12
а · б = 35
Мы можем использовать следующий синтаксис для вычисления скалярного произведения двух векторов на калькуляторе TI-84:
sum({2, 5, 6} \* {4, 3, 2})
В следующем пошаговом примере показано, как использовать этот синтаксис на практике.
Пример: расчет скалярного произведения на калькуляторе TI-84
Используйте следующие шаги, чтобы вычислить скалярное произведение между двумя векторами:
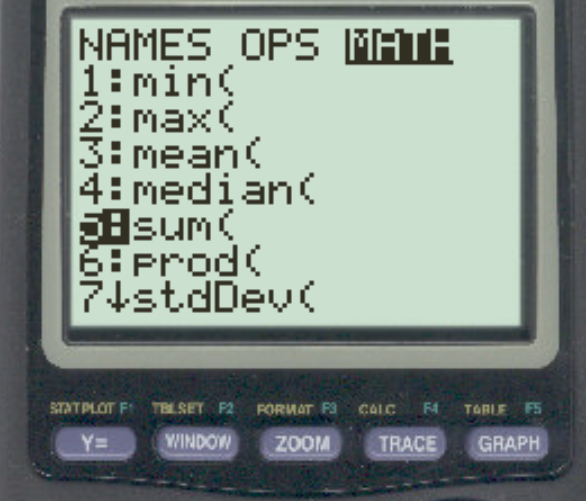
Шаг 1: Введите сумму (команда.
Сначала нажмите 2nd , затем нажмите STAT , затем перейдите к MATH и нажмите sum :
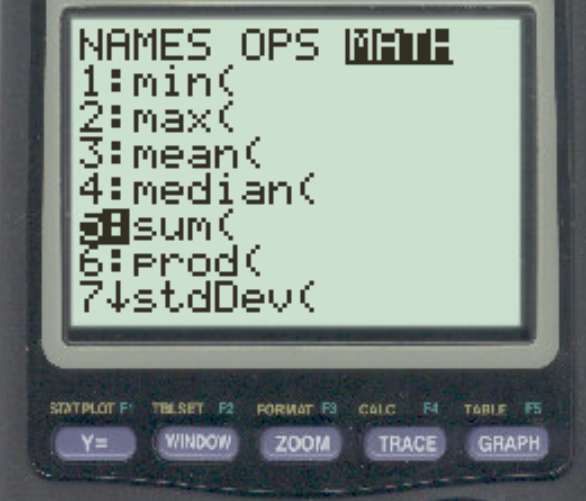
Шаг 2: Введите левую фигурную скобку.
Затем нажмите 2 , затем нажмите ( , чтобы ввести первую фигурную скобку:
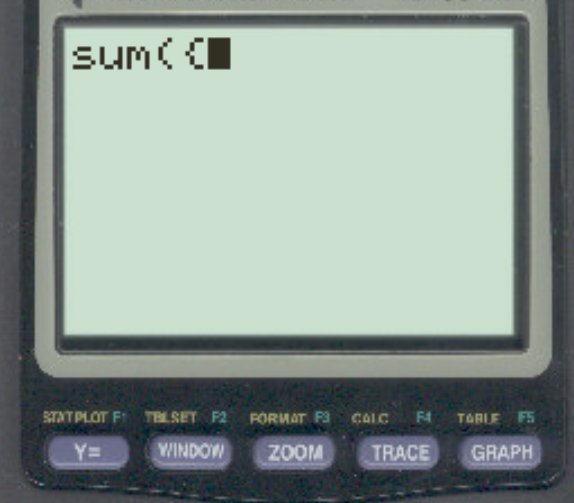
Шаг 3: введите данные
Затем введите следующие значения для каждого вектора:
- Вектор а: 2, 5, 6
- Вектор б: 4, 3, 2
Обязательно включите знак умножения между двумя векторами и закройте конец команды sum() скобкой справа. Затем нажмите ВВОД :
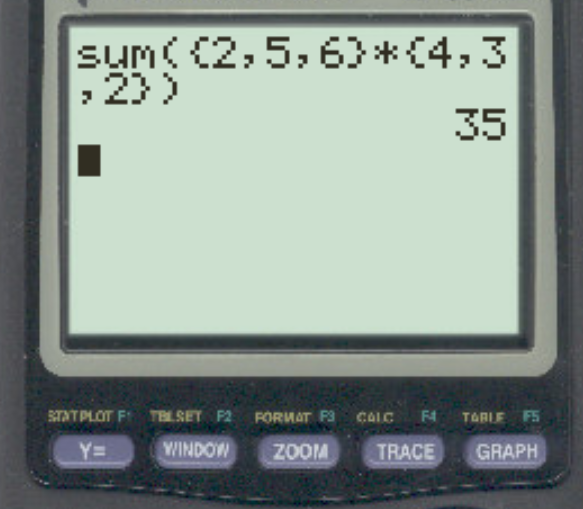
Скалярный продукт оказывается равным 35.Это соответствует значению, которое мы рассчитали вручную.
Дополнительные ресурсы
Как рассчитать скалярный продукт в Excel
Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R