В статистике мы часто хотим знать, насколько разные наблюдения влияют на регрессионные модели.
Одним из способов расчета влияния наблюдений является использование метрики, известной как DFBETAS , которая сообщает нам стандартизированный эффект удаления каждого отдельного наблюдения на каждый коэффициент.
Эта метрика дает нам представление о том, насколько каждое наблюдение влияет на оценку каждого коэффициента в данной регрессионной модели.
В этом руководстве показан пошаговый пример расчета и визуализации DFBETAS для каждого наблюдения в модели в R.
Шаг 1: Постройте модель регрессии
Во-первых, мы построим модель множественной линейной регрессии, используя встроенный набор данных mtcars в R:
#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)
#view model summary
summary(model)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.735904 1.331566 23.083 < 2e-16 \*\*\*
disp -0.030346 0.007405 -4.098 0.000306 \*\*\*
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
Шаг 2: Рассчитайте DFBETAS для каждого наблюдения
Далее мы будем использовать встроенную функцию dfbetas() для вычисления значений DFBETAS для каждого наблюдения в модели:
#calculate DFBETAS for each observation in the model
dfbetas <- as.data.frame (dfbetas(model))
#display DFBETAS for each observation
dfbetas
(Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02
Для каждого наблюдения мы можем увидеть разницу в оценке коэффициента для точки пересечения, переменной disp и переменной hp , которая возникает, когда мы удаляем это конкретное наблюдение.
Обычно мы считаем, что наблюдение сильно влияет на оценку данного коэффициента, если его значение DBETAS превышает пороговое значение 2/√ n , где n — количество наблюдений.
В этом примере порог будет равен 0,3535534 :
#find number of observations
n <- nrow (mtcars)
#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)
thresh
[1] 0.3535534
Шаг 3: Визуализируйте DFBETAS
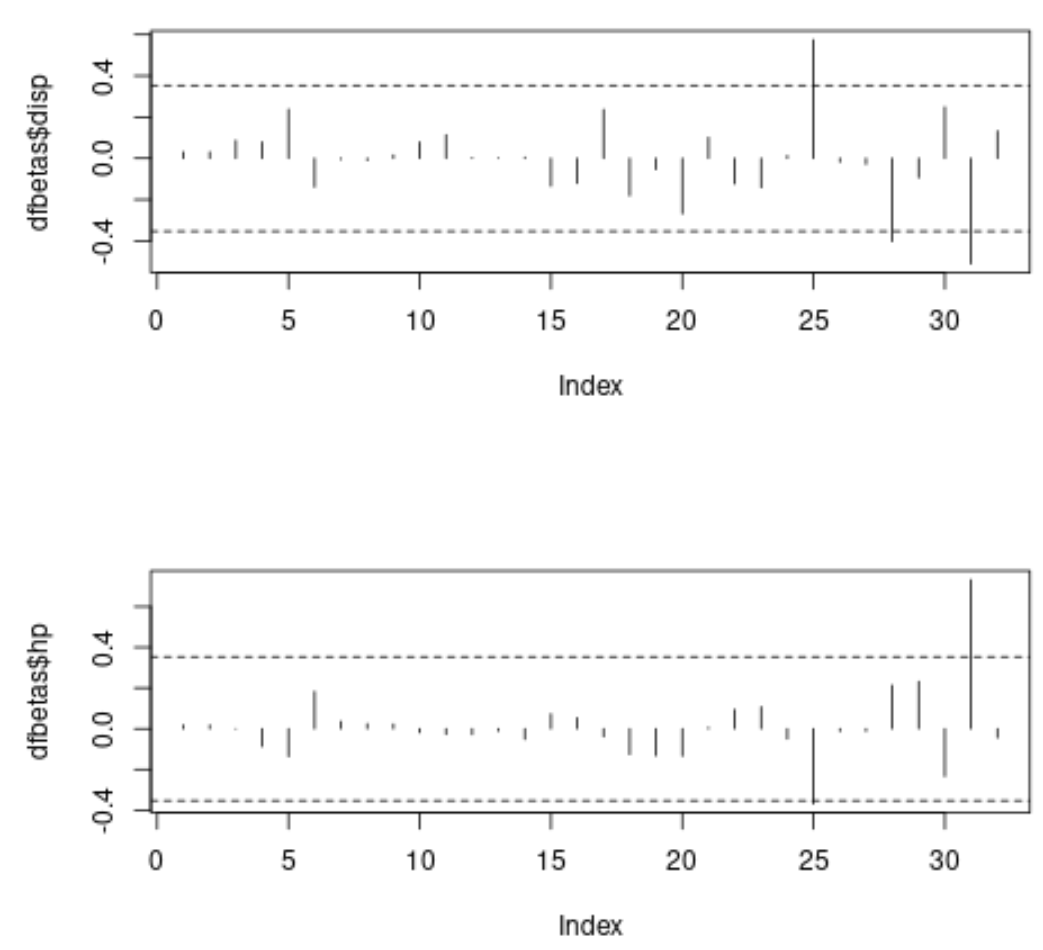
Наконец, мы можем создать графики для визуализации значения DFBETAS для каждого наблюдения и для каждого предиктора в модели:
#specify 2 rows and 1 column in plotting region
par(mfrow=c(2,1))
#plot DFBETAS for *disp* with threshold lines
plot(dfbetas$disp, type='h')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)
#plot DFBETAS for *hp* with threshold lines
plot(dfbetas$hp, type='h')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)
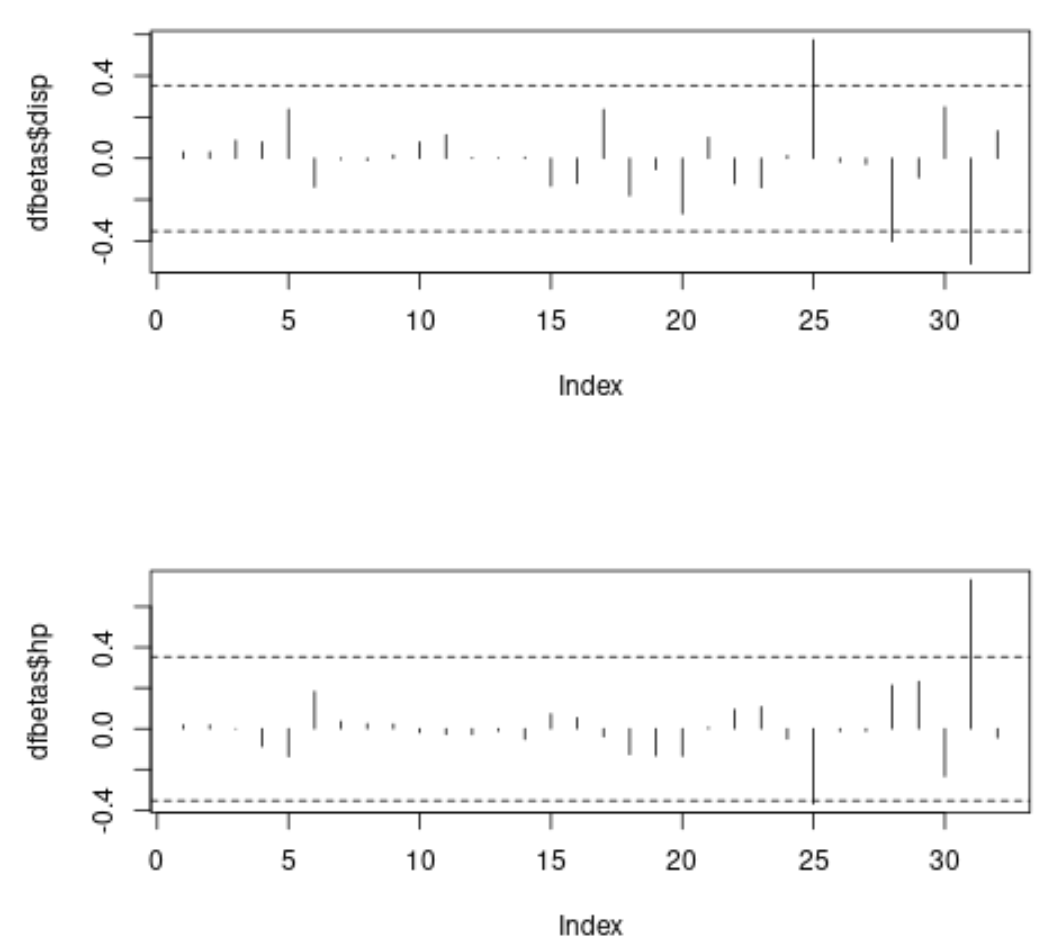
На каждом графике ось x отображает индекс каждого наблюдения в наборе данных, а значение y отображает соответствующий DFBETAS для каждого наблюдения и каждого предиктора.
На первом графике мы видим, что три наблюдения превышают абсолютное значение порога 0,3535534, а на втором графике мы видим, что два наблюдения превышают абсолютное значение порога.
Мы можем решить изучить эти наблюдения более тщательно, чтобы определить, не оказывают ли они чрезмерное влияние на оценку коэффициентов в модели.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как рассчитать статистику кредитного плеча в R
Как рассчитать DFFITS в R