Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между одной независимой переменной и одной переменной отклика .
В двух словах, этот метод находит линию, которая лучше всего «соответствует» данным, и принимает следующий вид:
ŷ = б 0 + б 1 х
куда:
- ŷ : Расчетное значение отклика
- b 0 : точка пересечения линии регрессии
- b 1 : Наклон линии регрессии
Это уравнение может помочь нам понять взаимосвязь между объясняющей переменной и переменной отклика, и (при условии, что она статистически значима) его можно использовать для прогнозирования значения переменной отклика при заданном значении объясняющей переменной.
В этом руководстве представлено пошаговое объяснение того, как выполнить простую линейную регрессию в R.
Шаг 1: Загрузите данные
В этом примере мы создадим поддельный набор данных, содержащий следующие две переменные для 15 студентов:
- Общее количество часов, отработанных для некоторого экзамена
- Оценка экзамена
Мы попытаемся подогнать простую модель линейной регрессии, используя часы в качестве объясняющей переменной и экзаменационный балл в качестве переменной ответа.
Следующий код показывает, как создать этот поддельный набор данных в R:
#create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))
#view first six rows of dataset
head(df)
hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81
#attach dataset to make it more convenient to work with
attach(df)
Шаг 2: Визуализируйте данные
Прежде чем мы подберем простую модель линейной регрессии, мы должны сначала визуализировать данные, чтобы понять их.
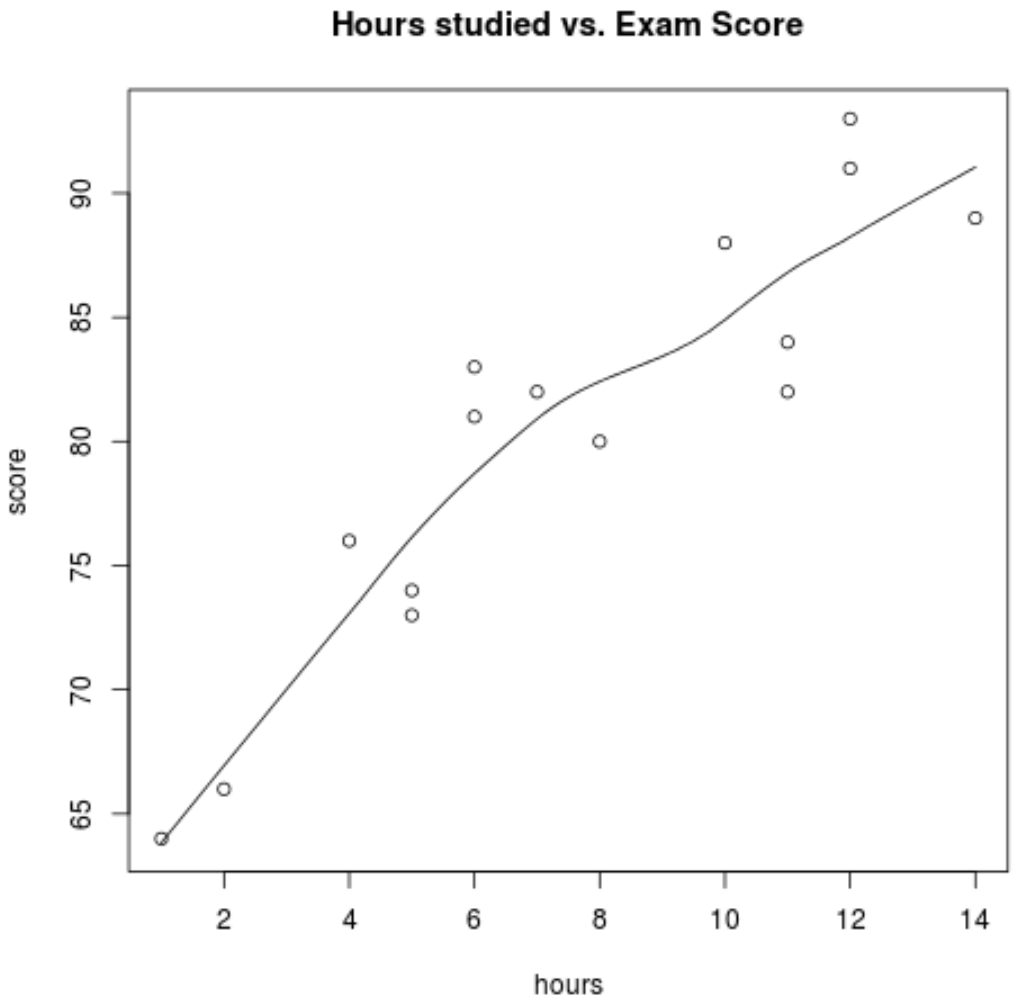
Во-первых, мы хотим удостовериться, что связь между часами и счетом примерно линейна, так как это основное допущение простой линейной регрессии. Мы можем создать простую диаграмму рассеяния , чтобы просмотреть взаимосвязь между двумя переменными:
scatter.smooth(hours, score, main='Hours studied vs. Exam Score')
Из графика видно, что зависимость кажется линейной. По мере увеличения количества часов оценка также имеет тенденцию к линейному увеличению.
Затем мы можем создать блочную диаграмму, чтобы визуализировать распределение результатов экзаменов и проверить наличие выбросов.По умолчанию R определяет наблюдение как выброс, если оно в 1,5 раза превышает межквартильный размах, превышающий третий квартиль (Q3), или в 1,5 раза превышает межквартильный размах, чем первый квартиль (Q1).
Если наблюдение является выбросом, на диаграмме появится крошечный кружок:
boxplot(score)
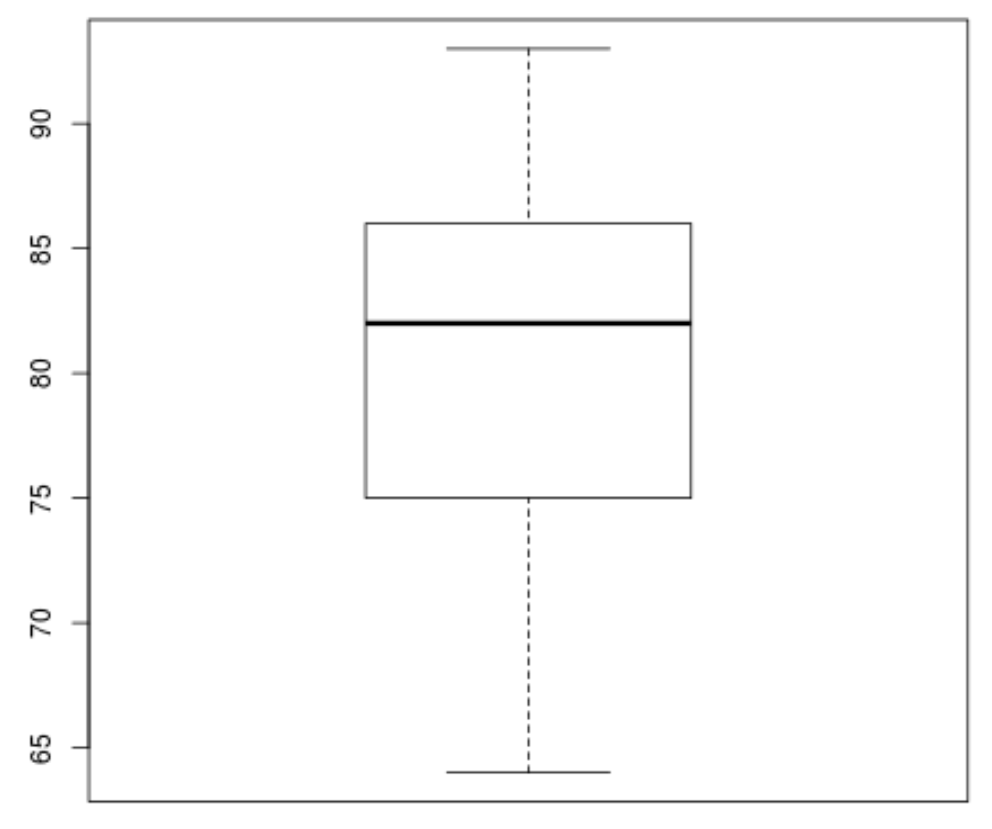
На диаграмме нет крошечных кружков, что означает, что в нашем наборе данных нет выбросов.
Шаг 3: выполните простую линейную регрессию
После того, как мы убедились, что взаимосвязь между нашими переменными является линейной и что нет никаких выбросов, мы можем приступить к подгонке простой модели линейной регрессии, используя часы в качестве объясняющей переменной и оценку в качестве переменной ответа:
#fit simple linear regression model
model <- lm(score~hours)
#view model summary
summary(model)
Call:
lm(formula = score ~ hours)
Residuals:
Min 1Q Median 3Q Max
-5.140 -3.219 -1.193 2.816 5.772
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 65.334 2.106 31.023 1.41e-13 \*\*\*
hours 1.982 0.248 7.995 2.25e-06 \*\*\*
---
Signif. codes: 0 '\*\*\*' 0.001 '\*\*' 0.01 '\*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
Из сводки модели мы видим, что подобранное уравнение регрессии:
Оценка = 65,334 + 1,982 * (часы)
Это означает, что каждый дополнительный час обучения связан со средним повышением экзаменационного балла на 1,982 балла. А значение отрезка 65,334 говорит нам о среднем ожидаемом экзаменационном балле для студента, который учится ноль часов.
Мы также можем использовать это уравнение, чтобы найти ожидаемую оценку экзамена на основе количества часов, которые изучает студент. Например, студент, который занимается 10 часов, должен получить экзаменационный балл 85,15 :
Оценка = 65,334 + 1,982 * (10) = 85,15
Вот как интерпретировать остальную часть сводки модели:
- Pr(>|t|): это значение p, связанное с коэффициентами модели. Поскольку p-значение для часов (2,25e-06) значительно меньше 0,05, мы можем сказать, что существует статистически значимая связь между часами и оценкой .
- Множественный R-квадрат: это число говорит нам о том, какую процентную вариацию в экзаменационных баллах можно объяснить количеством часов обучения. В целом, чем больше значение R-квадрата регрессионной модели, тем лучше независимые переменные способны предсказать значение переменной отклика. В этом случае 83,1% вариации баллов можно объяснить часами изучения.
- Остаточная стандартная ошибка: это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. Чем ниже это значение, тем точнее линия регрессии может соответствовать наблюдаемым данным. В этом случае средний наблюдаемый экзаменационный балл на 3,641 балла меньше, чем результат, предсказанный линией регрессии.
- F-статистика и p-значение: F-статистика ( 63,91 ) и соответствующее значение p ( 2,253e-06 ) говорят нам об общей значимости регрессионной модели, т. е. о том, полезны ли независимые переменные в модели для объяснения вариации. в переменной ответа. Поскольку p-значение в этом примере меньше 0,05, наша модель является статистически значимой, и считается, что часы полезны для объяснения вариаций в баллах .
Шаг 4: Создайте остаточные графики
После того, как мы подогнали простую модель линейной регрессии к данным, последним шагом является создание остаточных графиков.
Одно из ключевых предположений линейной регрессии состоит в том, что остатки регрессионной модели примерно нормально распределены и гомоскедастичны на каждом уровне объясняющей переменной. Если эти допущения нарушаются, то результаты нашей регрессионной модели могут вводить в заблуждение или быть ненадежными.
Чтобы убедиться, что эти предположения выполняются, мы можем построить следующие остаточные графики:
График остаточных и подобранных значений: этот график полезен для подтверждения гомоскедастичности. На оси X отображаются подогнанные значения, а на оси Y — остатки. Пока остатки кажутся случайно и равномерно распределенными по диаграмме вокруг нулевого значения, мы можем предположить, что гомоскедастичность не нарушена:
#define residuals
res <- resid(model)
#produce residual vs. fitted plot
plot(fitted(model), res)
#add a horizontal line at 0
abline(0,0)
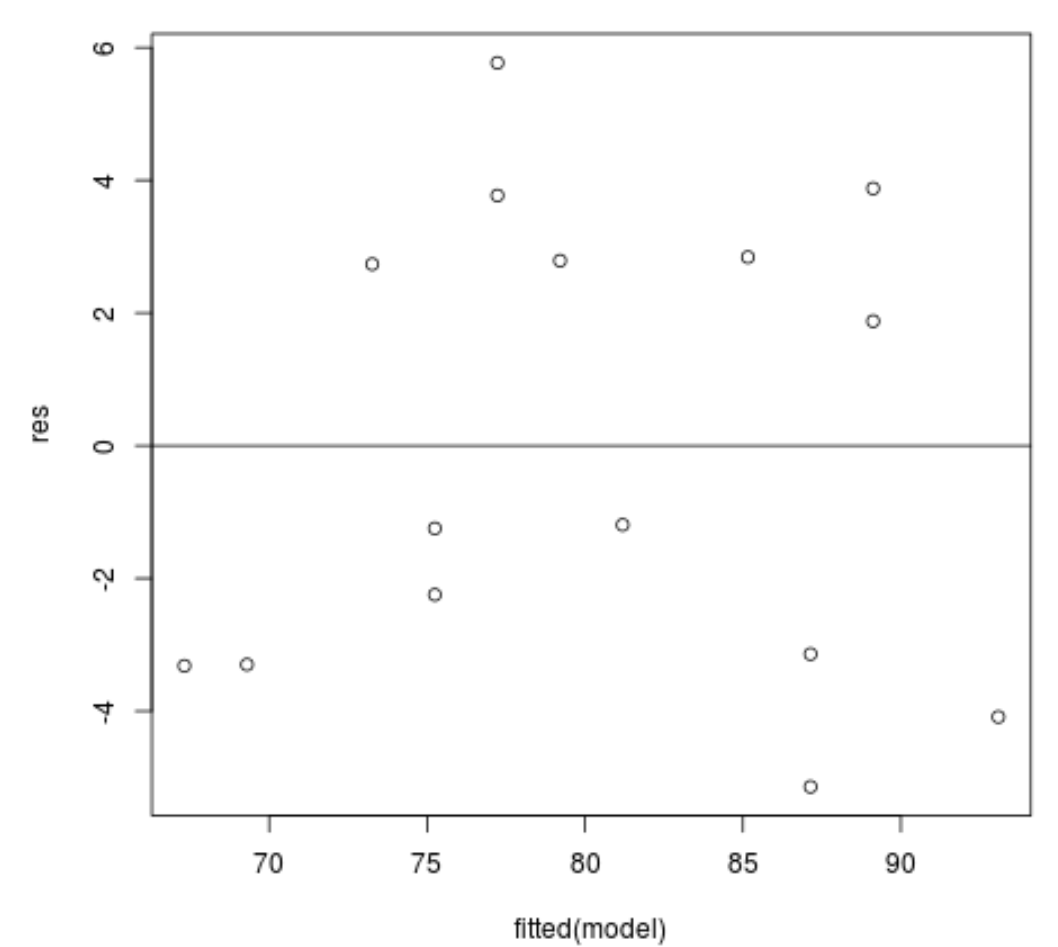
Остатки кажутся случайным образом разбросанными вокруг нуля и не демонстрируют каких-либо заметных закономерностей, так что это предположение выполняется.
График QQ: этот график полезен для определения того, следуют ли остатки нормальному распределению. Если значения данных на графике падают примерно по прямой линии под углом 45 градусов, то данные распределяются нормально:
#create Q-Q plot for residuals
qqnorm(res)
#add a straight diagonal line to the plot
qqline(res)
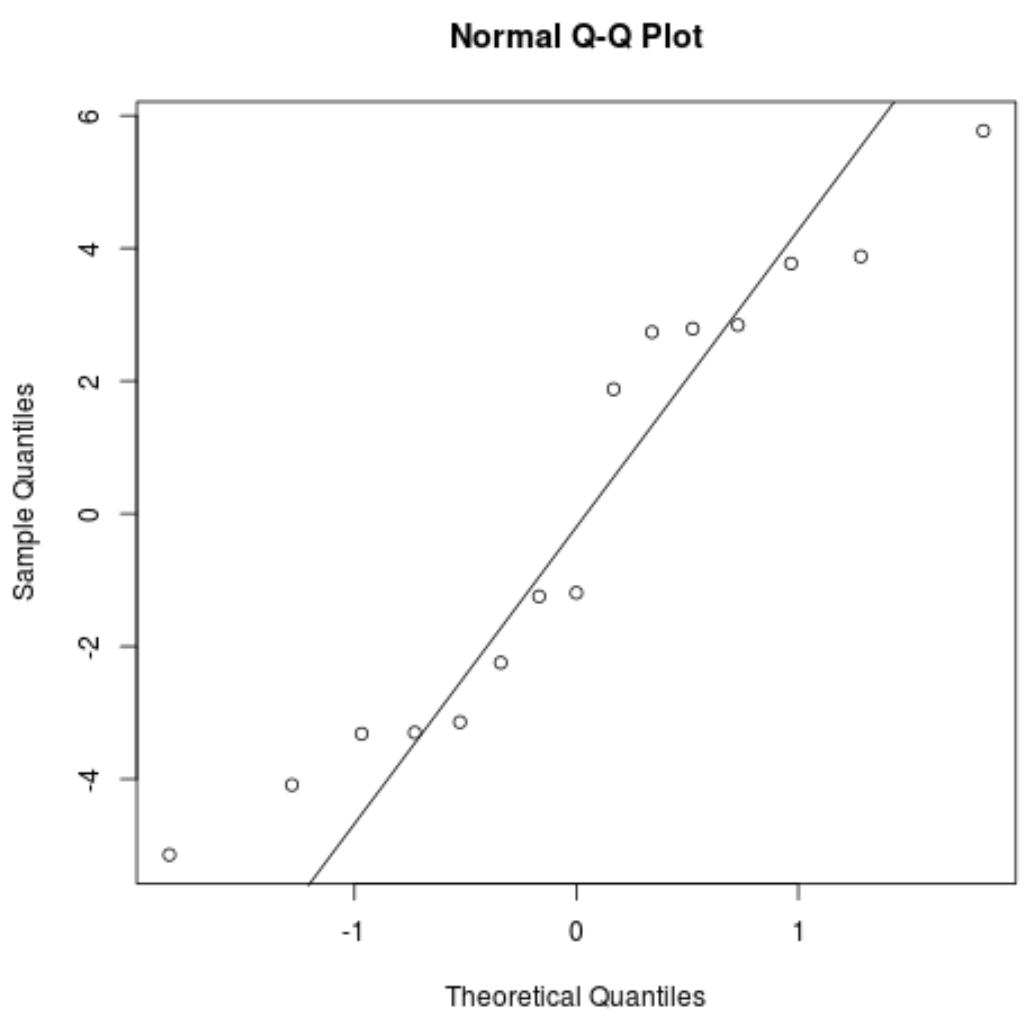
Остатки немного отклоняются от 45-градусной линии, но не настолько, чтобы вызывать серьезное беспокойство. Можно считать, что условие нормальности выполнено.
Поскольку остатки нормально распределены и гомоскедастичны, мы проверили выполнение допущений модели простой линейной регрессии. Таким образом, вывод нашей модели надежен.
Полный код R, использованный в этом руководстве, можно найти здесь .