Вы можете быстро сгенерировать нормальное распределение в R, используя функцию rnorm() , которая использует следующий синтаксис:
rnorm(n, mean=0, sd=1)
куда:
- n: количество наблюдений.
- среднее значение: среднее значение нормального распределения. По умолчанию 0.
- sd: стандартное отклонение нормального распределения. По умолчанию 1.
В этом руководстве показан пример использования этой функции для создания нормального распределения в R.
Связанный: Руководство по dnorm, pnorm, qnorm и rnorm в R
Пример: создание нормального распределения в R
Следующий код показывает, как создать нормальное распределение в R:
#make this example reproducible
set.seed(1)
#generate sample of 200 obs. that follows normal dist. with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)
#view first 6 observations in sample
head(data)
[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595
Мы можем быстро найти среднее значение и стандартное отклонение этого распределения:
#find mean of sample
mean(data)
[1] 10.10662
#find standard deviation of sample
sd(data)
[1] 2.787292
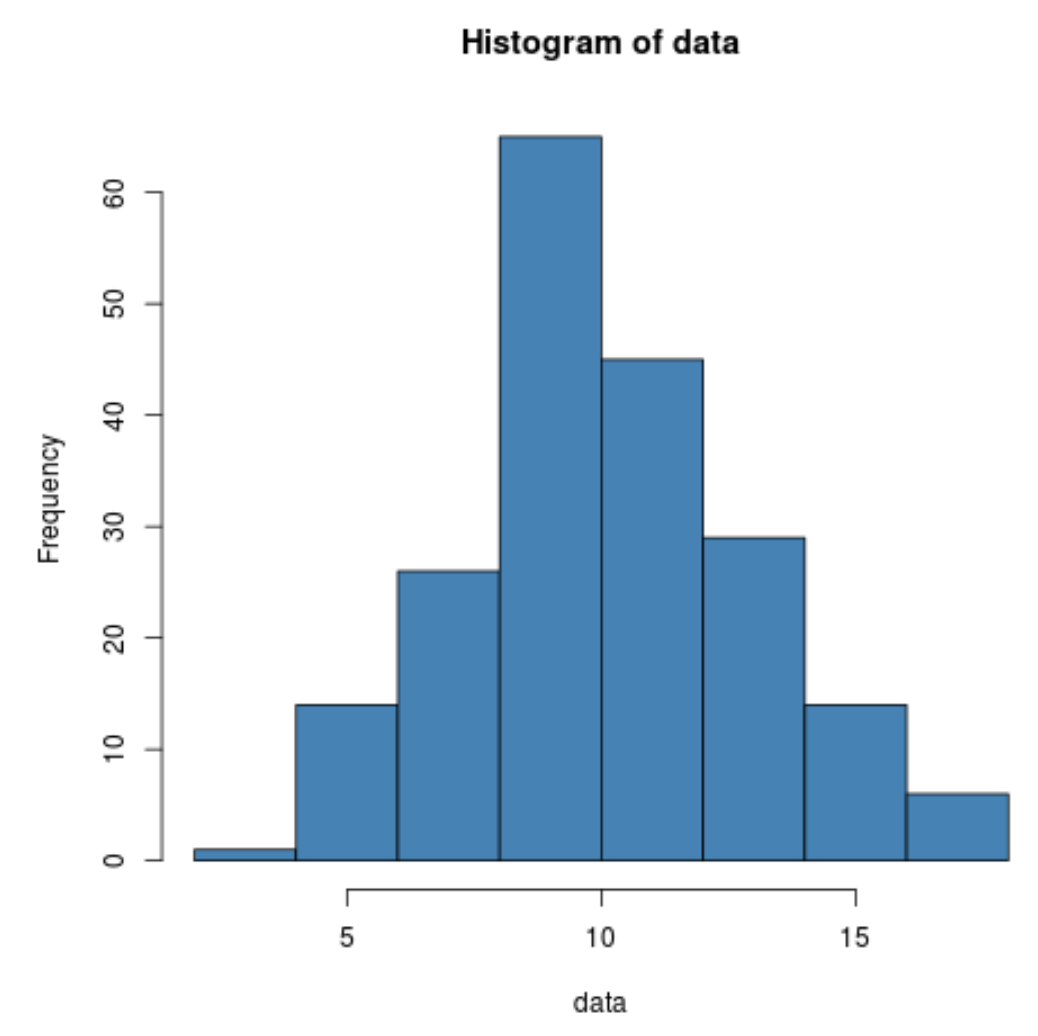
Мы также можем создать быструю гистограмму для визуализации распределения значений данных:
hist(data, col='steelblue')
Мы даже можем выполнить тест Шапиро-Уилка, чтобы увидеть, исходит ли набор данных из нормальной популяции:
shapiro.test(data)
Shapiro-Wilk normality test
data: data
W = 0.99274, p-value = 0.4272
Значение p теста оказывается равным 0,4272.Поскольку это значение не меньше 0,05, мы можем предположить, что данные выборки получены из населения с нормальным распределением.
Этот результат не должен вызывать удивления, поскольку мы генерировали данные с помощью функции rnorm() , которая естественным образом генерирует случайную выборку данных из нормального распределения.
Дополнительные ресурсы
Как построить нормальное распределение в R
Руководство по dnorm, pnorm, qnorm и rnorm в R
Как выполнить тест Шапиро-Уилка на нормальность в R