Тест Шапиро-Уилка является тестом на нормальность. Он используется для определения того, соответствует ли выборка нормальному распределению .
Этот тип теста полезен для определения того, исходит ли данный набор данных из нормального распределения, что является распространенным предположением, используемым во многих статистических тестах, включая регрессию , дисперсионный анализ , t-тесты и многие другие.
Мы можем легко выполнить тест Шапиро-Уилка для данного набора данных, используя следующую встроенную функцию в R:
Шапиро.тест(х)
куда:
- x: числовой вектор значений данных.
Эта функция создает тестовую статистику W вместе с соответствующим p-значением. Если p-значение меньше, чем α = 0,05, имеется достаточно доказательств, чтобы сказать, что выборка не происходит из населения с нормальным распределением.
Примечание. Размер выборки должен быть от 3 до 5000, чтобы можно было использовать функцию shapiro.test().
В этом руководстве показано несколько примеров использования этой функции на практике.
Пример 1. Критерий Шапиро-Уилка для нормальных данных
В следующем коде показано, как выполнить тест Шапиро-Уилка для набора данных с размером выборки n = 100:
#make this example reproducible
set.seed(0)
#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)
#perform Shapiro-Wilk test for normality
shapiro.test(data)
Shapiro-Wilk normality test
data: data
W = 0.98957, p-value = 0.6303
Значение p теста оказывается равным 0,6303.Поскольку это значение не меньше 0,05, мы можем предположить, что данные выборки получены из населения с нормальным распределением.
Этот результат не должен вызывать удивления, поскольку мы сгенерировали выборочные данные с помощью функции rnorm(), которая генерирует случайные значения из нормального распределения со средним значением = 0 и стандартным отклонением = 1.
Связанный: Руководство по dnorm, pnorm, qnorm и rnorm в R
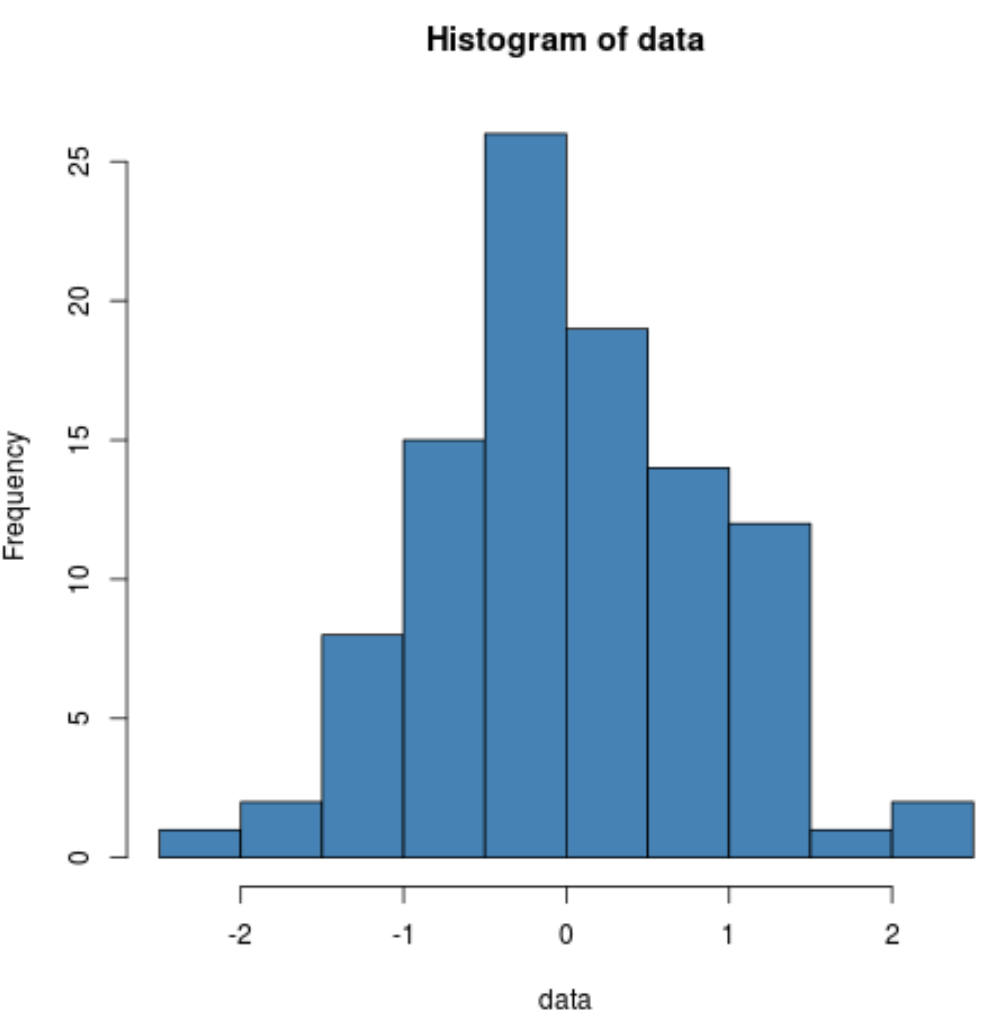
Мы также можем создать гистограмму, чтобы визуально убедиться, что данные выборки распределены нормально:
hist(data, col='steelblue')
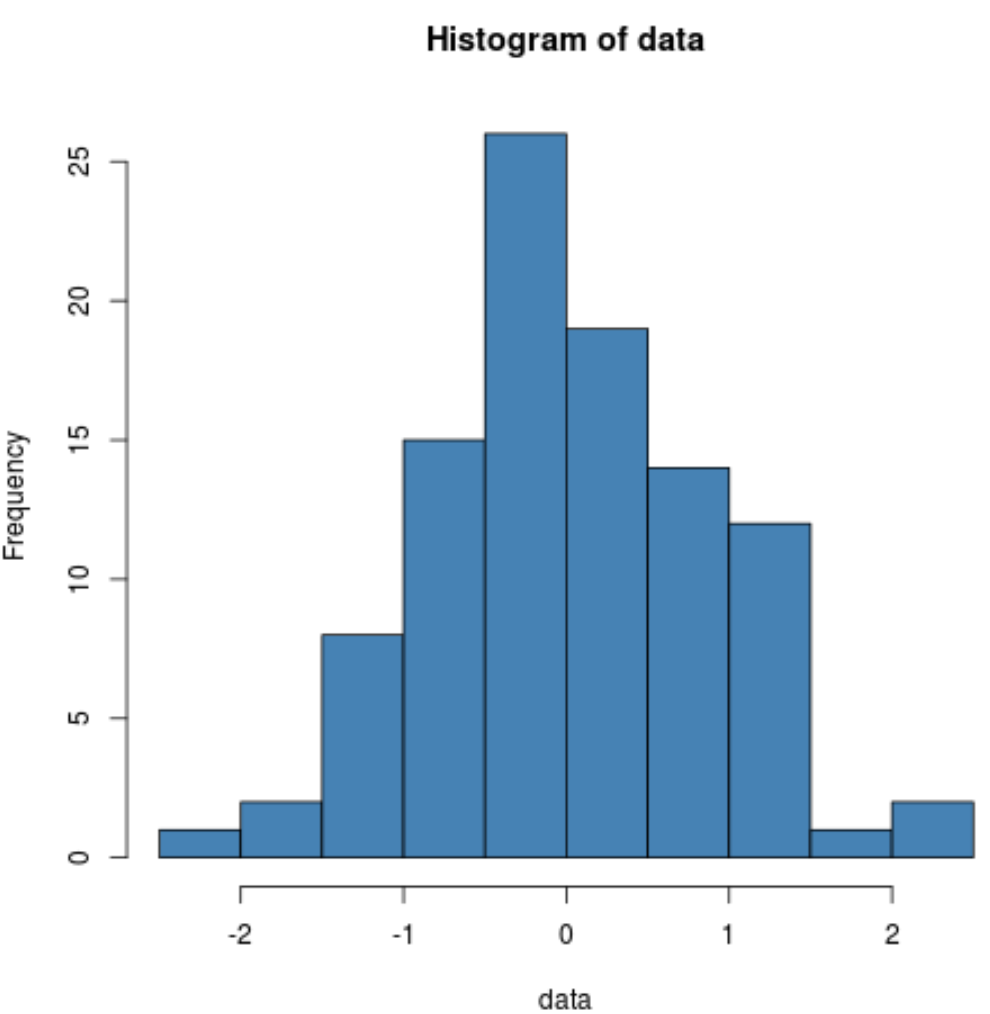
Мы видим, что распределение имеет довольно колоколообразную форму с одним пиком в центре распределения, что типично для данных с нормальным распределением.
Пример 2: тест Шапиро-Уилка на ненормальных данных
В следующем коде показано, как выполнить тест Шапиро-Уилка для набора данных с размером выборки n = 100, в котором значения генерируются случайным образом израспределения Пуассона :
#make this example reproducible
set.seed(0)
#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)
#perform Shapiro-Wilk test for normality
shapiro.test(data)
Shapiro-Wilk normality test
data: data
W = 0.94397, p-value = 0.0003393
Значение p теста оказывается равным 0,0003393.Поскольку это значение меньше 0,05, у нас есть достаточно доказательств, чтобы сказать, что данные выборки не получены из населения с нормальным распределением.
Этот результат не должен вызывать удивления, поскольку мы сгенерировали выборочные данные с помощью функции rpois(), которая генерирует случайные значения из распределения Пуассона.
Связанный: Руководство по dpois, ppois, qpois и rpois в R
Мы также можем создать гистограмму, чтобы визуально увидеть, что выборочные данные не распределены нормально:
hist(data, col='coral2')
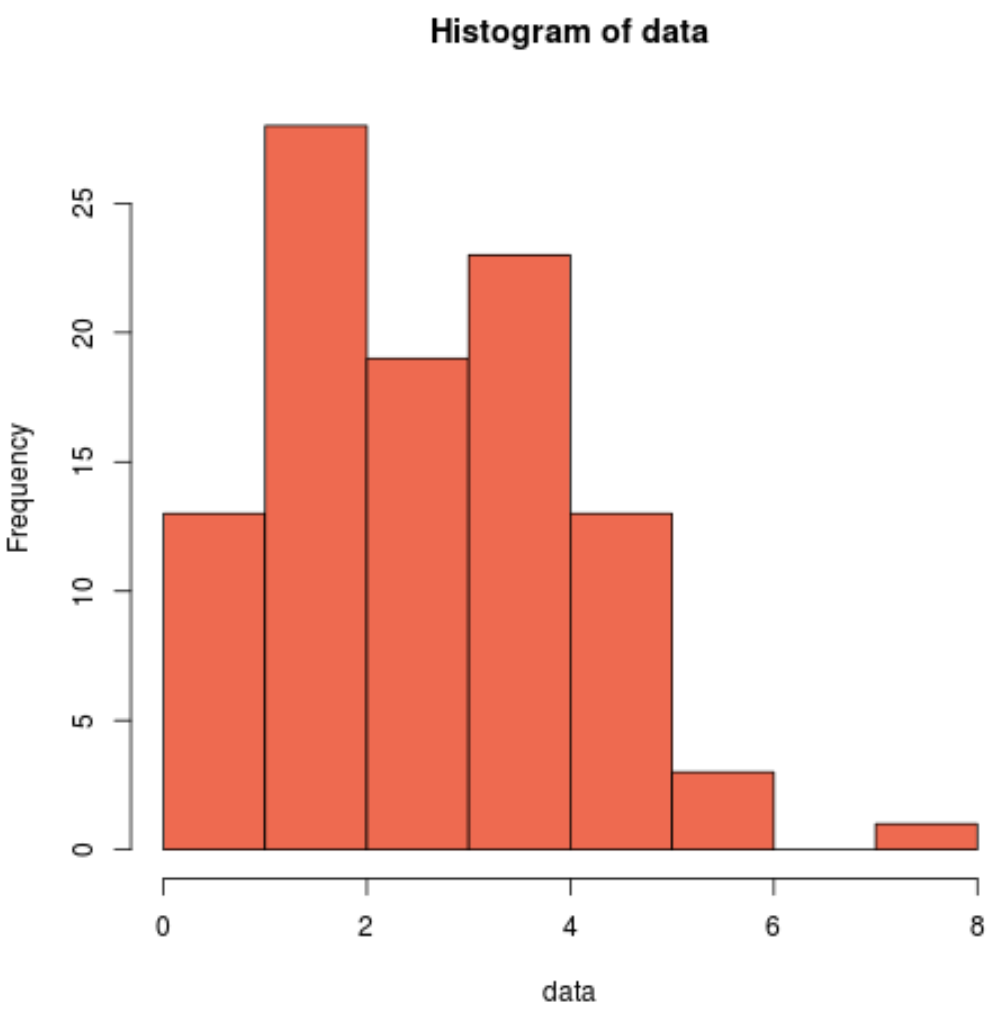
Мы видим, что распределение скошено вправо и не имеет типичной «колокольчатой формы», связанной с нормальным распределением. Таким образом, наша гистограмма соответствует результатам теста Шапиро-Уилка и подтверждает, что данные нашей выборки не имеют нормального распределения.
Что делать с ненормальными данными
Если данный набор данных не распределен нормально, мы часто можем выполнить одно из следующих преобразований, чтобы сделать его более нормальным:
1. Преобразование журнала: преобразование переменной ответа из y в log(y) .
2. Преобразование квадратного корня: преобразовать переменную отклика из y в √y .
3. Преобразование кубического корня: преобразовать переменную ответа из y в y 1/3 .
Выполняя эти преобразования, переменная отклика обычно становится ближе к нормально распределенной.
Ознакомьтесь с этим руководством , чтобы увидеть, как выполнять эти преобразования на практике.
Дополнительные ресурсы
Как провести тест Андерсона-Дарлинга в R
Как провести тест Колмогорова-Смирнова в R
Как выполнить тест Шапиро-Уилка в Python