Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.
Одна переменная x известна как предикторная переменная. Другая переменная, y , известна как переменная ответа .
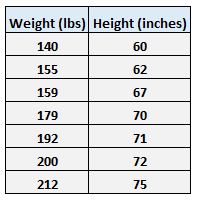
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:
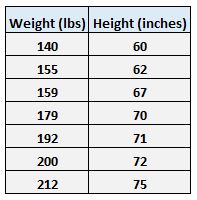
Пусть вес будет предикторной переменной, а рост — переменной отклика.
Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:

На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.
Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным:

Формула для этой линии наилучшего соответствия записывается так:
ŷ = б 0 + б 1 х
где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.
В этом примере линия наилучшего соответствия:
рост = 32,783 + 0,2001*(вес)
Как рассчитать остатки
Обратите внимание, что точки данных на нашей диаграмме рассеяния не всегда точно попадают на линию наилучшего соответствия:

Эта разница между точкой данных и линией называется остатком.Для каждой точки данных мы можем рассчитать остаток этой точки, взяв разницу между ее фактическим значением и прогнозируемым значением из линии наилучшего соответствия.
Пример 1: Расчет остатка
Например, вспомните вес и рост семи человек в нашем наборе данных:

Первая особь имеет вес 140 фунтов. и высотой 60 дюймов.
Чтобы узнать прогнозируемый рост для этого человека, мы можем подставить его вес в уравнение наилучшего соответствия:
рост = 32,783 + 0,2001*(вес)
Таким образом, прогнозируемый рост этого человека:
высота = 32,783 + 0,2001*(140)
высота = 60,797 дюйма
Таким образом, невязка для этой точки данных составляет 60 – 60,797 = -0,797 .
Пример 2: Расчет остатка
Мы можем использовать тот же самый процесс, который мы использовали выше, для вычисления невязки для каждой точки данных. Например, давайте рассчитаем остаток для второго человека в нашем наборе данных:

Второй человек имеет вес 155 фунтов. и высотой 62 дюйма.
Чтобы узнать прогнозируемый рост для этого человека, мы можем подставить его вес в уравнение наилучшего соответствия:
рост = 32,783 + 0,2001*(вес)
Таким образом, прогнозируемый рост этого человека:
высота = 32,783 + 0,2001*(155)
высота = 63,7985 дюйма
Таким образом, остаток для этой точки данных составляет 62 – 63,7985 = -1,7985 .
Вычисление всех остатков
Используя тот же метод, что и в предыдущих двух примерах, мы можем рассчитать остатки для каждой точки данных:

Обратите внимание, что некоторые остатки положительны, а некоторые отрицательны. Если мы сложим все остатки, они в сумме дадут ноль.
Это связано с тем, что линейная регрессия находит линию, которая минимизирует общие квадраты остатков, поэтому линия идеально проходит через данные, причем некоторые точки данных лежат над линией, а некоторые — под линией.
Визуализация остатков
Напомним, что невязка — это просто расстояние между фактическим значением данных и значением, предсказанным линией регрессии наилучшего соответствия. Вот как эти расстояния выглядят визуально на диаграмме рассеивания:

Обратите внимание, что некоторые остатки больше других. Кроме того, некоторые остатки положительны, а некоторые отрицательны, как мы упоминали ранее.
Создание остаточного графика
Весь смысл вычисления остатков состоит в том, чтобы увидеть, насколько хорошо линия регрессии соответствует данным.
Большие невязки указывают на то, что линия регрессии плохо соответствует данным, т. е. фактические точки данных не совпадают с линией регрессии.
Меньшие невязки указывают на то, что линия регрессии лучше соответствует данным, т. е. фактические точки данных располагаются близко к линии регрессии.
Одним из полезных типов графика для одновременной визуализации всех остатков является остаточный график. Остаточный график — это тип графика, который отображает прогнозируемые значения в сравнении с остаточными значениями для регрессионной модели.
Этот тип графика часто используется для оценки того, подходит ли модель линейной регрессии для данного набора данных, и для проверки гетероскедастичности остатков.
Ознакомьтесь с этим учебным пособием , чтобы узнать, как создать остаточный график для простой модели линейной регрессии в Excel.