Регрессионный анализ — это метод, который мы можем использовать для понимания взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .
Один из способов оценить, насколько хорошо регрессионная модель соответствует набору данных, — вычислить среднеквадратичную ошибку , которая представляет собой показатель, указывающий нам среднее расстояние между прогнозируемыми значениями из модели и фактическими значениями в наборе данных.
Чем ниже RMSE, тем лучше данная модель может «соответствовать» набору данных.
Формула для нахождения среднеквадратичной ошибки, часто обозначаемая аббревиатурой RMSE , выглядит следующим образом:
СКО = √ Σ(P i – O i ) 2 / n
куда:
- Σ — причудливый символ, означающий «сумма».
- P i - прогнозируемое значение для i -го наблюдения в наборе данных.
- O i - наблюдаемое значение для i -го наблюдения в наборе данных.
- n - размер выборки
В следующем примере показано, как интерпретировать RMSE для данной модели регрессии.
Пример: как интерпретировать RMSE для регрессионной модели
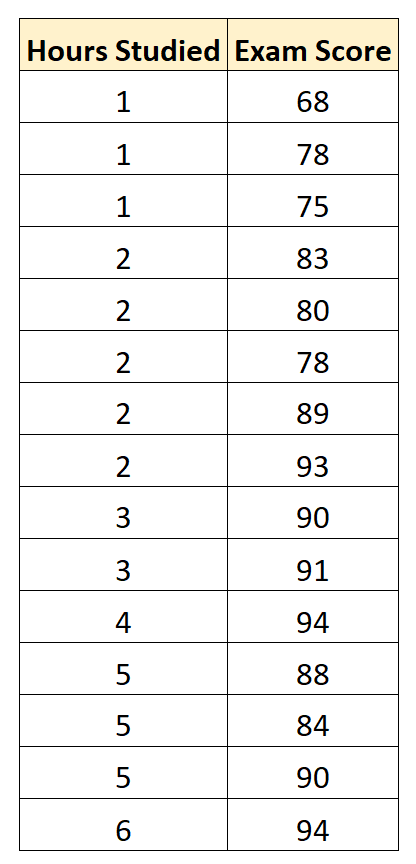
Предположим, мы хотим построить регрессионную модель, которая использует «учебные часы» для прогнозирования «экзаменационного балла» студентов на конкретном вступительном экзамене в колледж.
Мы собираем следующие данные для 15 студентов:
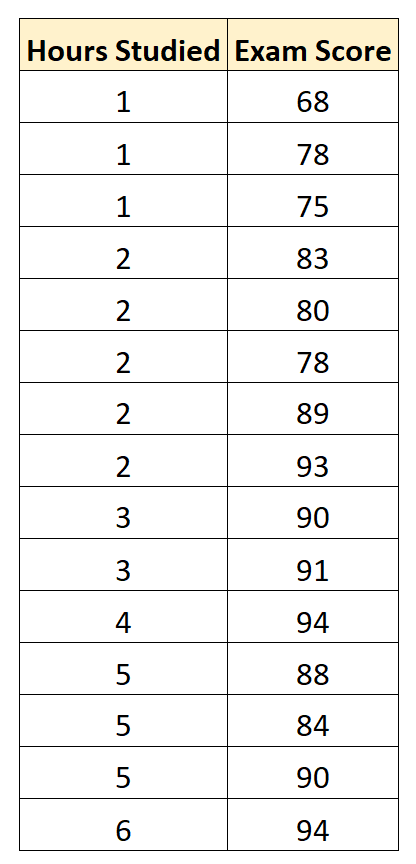
Затем мы используем статистическое программное обеспечение (например, Excel, SPSS, R, Python) и т. д., чтобы найти следующую подогнанную модель регрессии:
Экзаменационный балл = 75,95 + 3,08 * (часы обучения)
Затем мы можем использовать это уравнение, чтобы предсказать экзаменационную оценку каждого студента, исходя из того, сколько часов они учились:
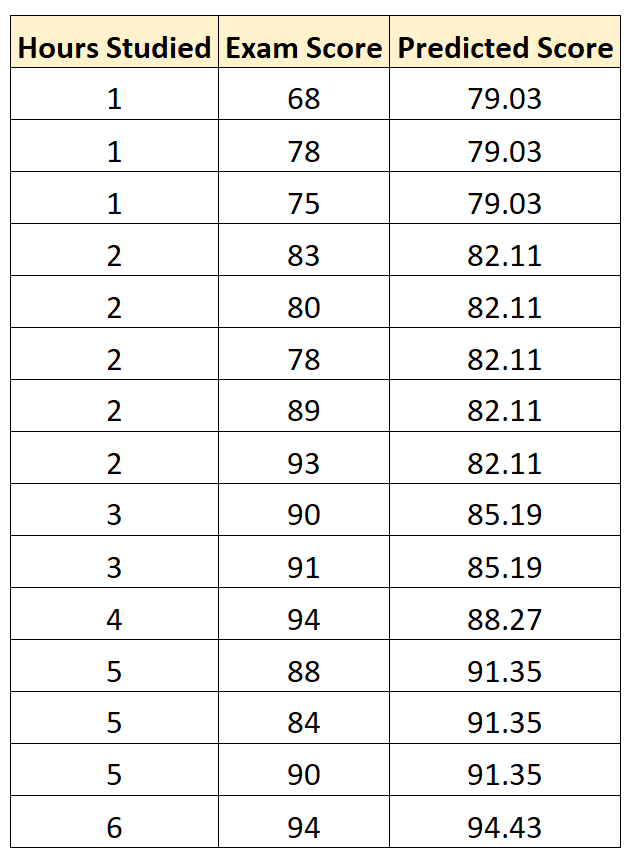
Затем мы можем вычислить квадрат разницы между каждой прогнозируемой оценкой экзамена и фактической оценкой экзамена. Затем мы можем извлечь квадратный корень из среднего значения этих разностей:
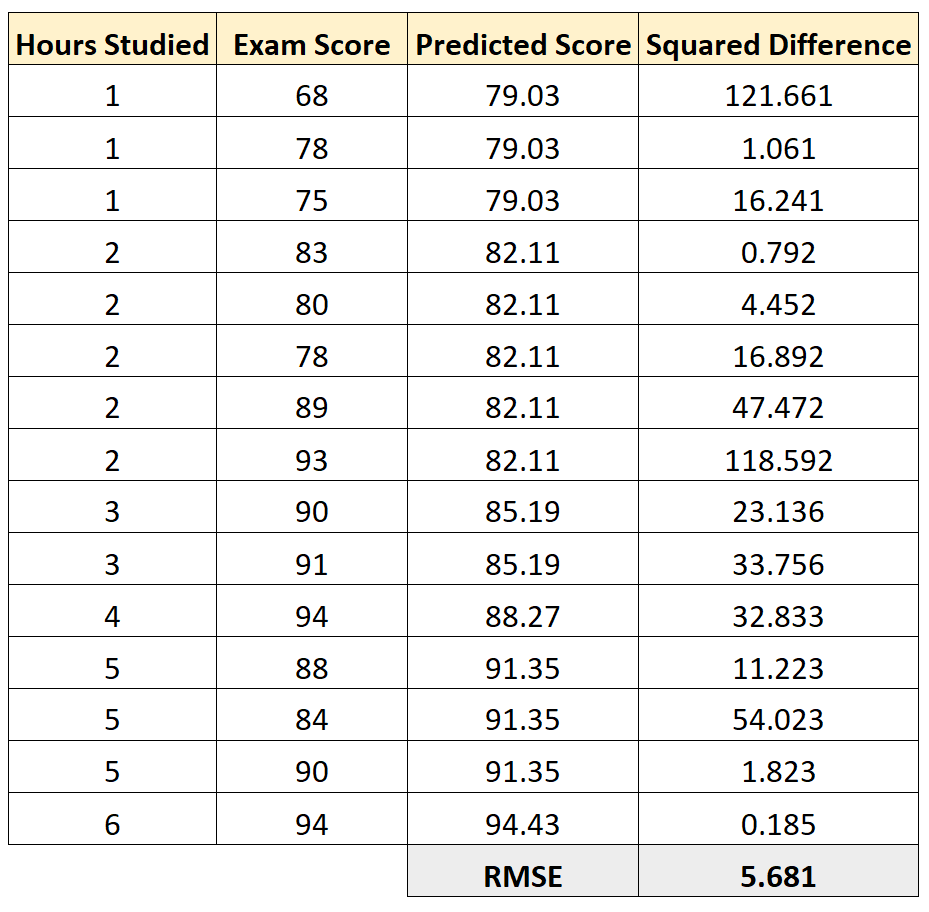
RMSE для этой регрессионной модели оказывается равным 5,681 .
Напомним, что остатки регрессионной модели представляют собой разницу между наблюдаемыми значениями данных и значениями, предсказанными моделью.
Остаток = (P i – O i )
куда
- P i - прогнозируемое значение для i -го наблюдения в наборе данных.
- O i - наблюдаемое значение для i -го наблюдения в наборе данных.
И помните, что RMSE регрессионной модели рассчитывается как:
СКО = √ Σ(P i – O i ) 2 / n
Это означает, что RMSE представляет собой квадратный корень из дисперсии остатков.
Это значение полезно знать, поскольку оно дает нам представление о среднем расстоянии между наблюдаемыми значениями данных и прогнозируемыми значениями данных.
Это отличается от R-квадрата модели, который сообщает нам долю дисперсии переменной отклика, которая может быть объяснена предикторной переменной (переменными) в модели.
Сравнение значений RMSE из разных моделей
RMSE особенно полезен для сравнения соответствия различных моделей регрессии.
Например, предположим, что мы хотим построить регрессионную модель, чтобы предсказать результаты экзаменов студентов, и мы хотим найти наилучшую возможную модель среди нескольких потенциальных моделей.
Предположим, мы подгоняем три разные модели регрессии и находим соответствующие им значения RMSE:
- RMSE модели 1: 14,5
- RMSE модели 2: 16,7
- RMSE модели 3: 9,8
Модель 3 имеет самый низкий RMSE, что говорит нам о том, что она способна лучше всего соответствовать набору данных из трех потенциальных моделей.
Дополнительные ресурсы
Калькулятор среднеквадратичной ошибки
Как рассчитать RMSE в Excel
Как рассчитать RMSE в R
Как рассчитать RMSE в Python