В статистике вероятность относится к вероятности того, что какое-то событие произойдет. Он рассчитывается как:
ВЕРОЯТНОСТЬ:
P(событие) = (# желаемых результатов) / (# возможных результатов)
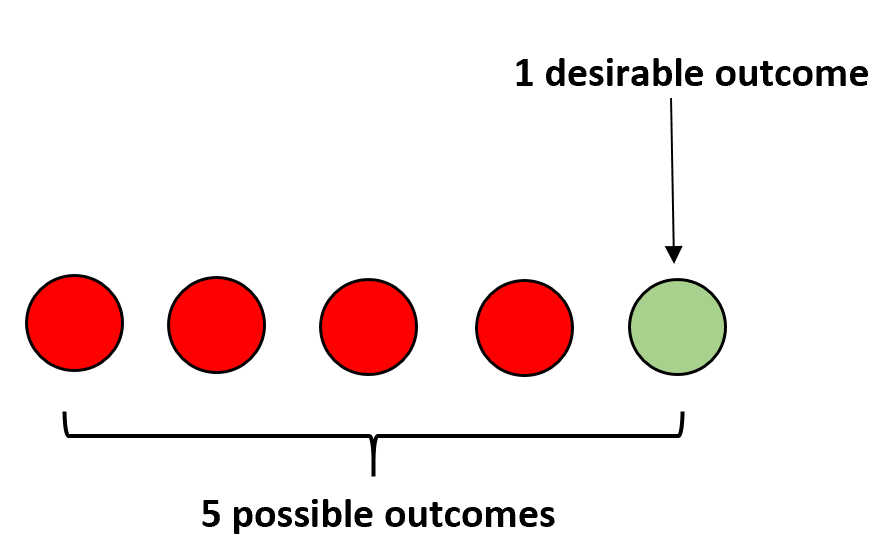
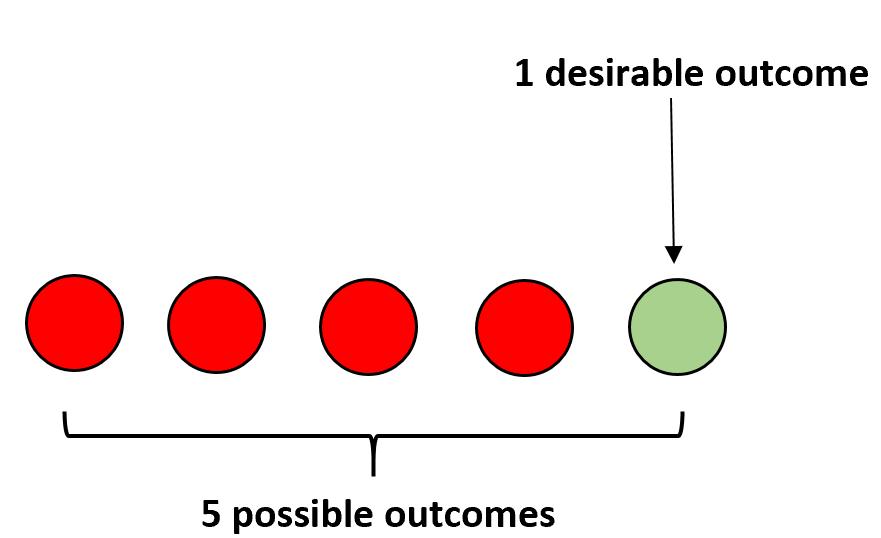
Например, предположим, что у нас есть четыре красных мяча и один зеленый мяч в мешке. Если вы закроете глаза и случайным образом выберете мяч, вероятность того, что вы выберете зеленый мяч, рассчитывается как:
P(зеленый) = 1/5 = 0,2 .
Шансы на то, что какое-то событие произойдет, можно рассчитать как:
ШАНСЫ:
Коэффициенты (событие) = P (событие происходит) / 1-P (событие происходит)
Например, вероятность того, что выпадет зеленый шар, равна (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .
Отношение шансов – это отношение двух шансов.
КОЭФФИЦИЕНТ СООТНОШЕНИЯ:
Отношение шансов = шансы события A / шансы события B
Например, мы могли бы рассчитать отношение шансов между выбором красного и зеленого шаров.
Вероятность того, что выпадет красный шар, равна 4/5 = 0,8 .
Вероятность того, что выпадет красный шар, равна (0,8)/1-(0,8) = 0,8/0,2 = 4 .
Отношение шансов выбора красного шара по сравнению с зеленым шаром рассчитывается как:
Шансы (красный) / Шансы (зеленый) = 4 / 0,25 = 16 .
Таким образом, шансы выбрать красный шар в 16 раз больше, чем шансы выбрать зеленый мяч.
Когда в реальном мире используются отношения шансов?
В реальном мире отношения шансов используются в различных условиях, когда исследователи хотят сравнить шансы двух событий. Вот несколько примеров.
Пример №1: интерпретация отношения шансов
Исследователи хотят знать, повышает ли новое лечение шансы пациента на положительный результат для здоровья по сравнению с существующим лечением. В следующей таблице показано количество пациентов с положительным или отрицательным результатом лечения в зависимости от лечения.

Вероятность того, что пациент испытает положительный результат при новом лечении, можно рассчитать как:
Коэффициенты = P(положительные) / 1 - P(положительные) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
Шансы пациента получить положительный результат при существующем лечении можно рассчитать как:
Шансы = P (положительный) / 1 - P (положительный) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Таким образом, отношение шансов получить положительный результат при новом лечении по сравнению с существующим лечением можно рассчитать как:
Отношение шансов = 1,25 / 0,875 = 1,428 .
Мы бы интерпретировали это как означающее, что вероятность того, что пациент испытает положительный результат при использовании нового лечения, в 1,428 раза превышает вероятность того , что пациент получит положительный результат при использовании существующего лечения.
Другими словами, шансы на положительный результат увеличиваются на 42,8% при новом лечении.
Пример № 2: интерпретация отношения шансов
Маркетологи хотят знать, побуждает ли одна реклама покупателей покупать определенный товар чаще, чем другая реклама, поэтому они показывают каждую рекламу 100 людям. В следующей таблице показано количество людей, купивших товар, в зависимости от того, какую рекламу они видели:
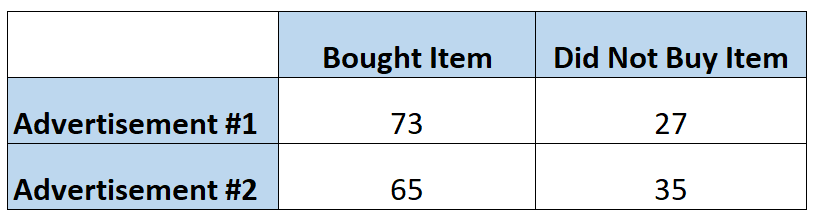
Вероятность того, что человек купит товар после того, как увидит первую рекламу, можно рассчитать как:
Шансы = P(куплено) / 1 – P(куплено) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
Вероятность того, что человек купит товар после просмотра второй рекламы, можно рассчитать как:
Шансы = P(куплено) / 1 – P(куплено) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Таким образом, отношение шансов для покупателя, купившего товар после просмотра первой рекламы, по сравнению с покупкой после просмотра второй рекламы, можно рассчитать как:
Отношение шансов = 2,704 / 1,857 = 1,456 .
Мы бы интерпретировали это так, что вероятность того, что человек купит товар после просмотра первой рекламы, в 1,456 раз превышает вероятность того , что человек купит товар после просмотра второй рекламы.
Другими словами, шансы купить предмет увеличиваются на 45,6% при использовании первой рекламы.
Дополнительные ресурсы
Как рассчитать отношение шансов и относительный риск в Excel
Как интерпретировать отношение шансов меньше 1
Как интерпретировать относительный риск